
- •Часть 1 Занятие 1. Тема: «Двойной интеграл. Повторное интегрирование».
- •3. В аудитории.
- •4. Задачи для самостоятельной работы.
- •Занятие 2. Тема: «Замена переменной в двойном интеграле».
- •2. В аудитории.
- •3. Задачи для самостоятельной работы.
- •Занятие 3. Тема: «Приложение двойного интеграла».
- •1. Геометрические приложения двойных интегралов.
- •3. В аудитории.
- •4. Задачи для самостоятельной работы.
- •Занятие 4. Тема: «Тройной интеграл».
- •4. В аудитории.
- •4. Задачи для самостоятельной работы.
- •Занятие 5. Тема: «Криволинейный интеграл 1-го рода, приложения».
- •3. В аудитории.
- •4. Задачи для самостоятельной работы.
- •Занятие 6. Тема: «Криволинейный интеграл 2-го рода, формула Грина, приложения».
- •2. Вычисление криволинейного интеграла 2-го рода с помощью определенного интеграла.
- •3. Связь между криволинейными интегралами 1-го и 2-го рода.
- •4. Формула Грина.
- •5. Условия независимости криволинейного интеграла 2-го рода от пути интегрирования.
- •5. В аудитории.
- •6. Задачи для самостоятельной работы.
- •Занятия 7-8 (дополнителные). Тема: «Поверхностный интеграл, формулы Стокса, Остроградского - Гаусса».
- •2. Поверхностные интегралы 1-го рода.
- •6. В аудитории.
- •7. Задачи для самостоятельной работы.
- •Часть 2
- •2 Вариант
- •3 Вариант
- •4 Вариант
- •Уровень б
- •5 Вариант
Часть 1 Занятие 1. Тема: «Двойной интеграл. Повторное интегрирование».
1.
Определение двойного интеграла.
Пусть функция
 определена на измеримом по Жордану
множестве
определена на измеримом по Жордану
множестве
 на плоскости
на плоскости
 .
Разобьем
на
.
Разобьем
на
 измеримых по Жордану и попарно
непересекающихся частей
измеримых по Жордану и попарно
непересекающихся частей
 .
В каждой части
.
В каждой части
 возьмем произвольную точку
возьмем произвольную точку
 и составим сумму
и составим сумму
 ,
,
где
 - площадь
.
Эта сумма называется интегральной
суммой
функции
- площадь
.
Эта сумма называется интегральной
суммой
функции
 соответствующей данному разбиению
множества
на части
и данному выбору промежуточных точек
соответствующей данному разбиению
множества
на части
и данному выбору промежуточных точек
 .
.
Диаметром
множества
точек назовем точную верхнюю грань
расстояний между двумя произвольными
точками этого множества:
 .
.
Пусть
 .
.
Определение.
Число
 называется пределом
интегральных сумм
называется пределом
интегральных сумм
 при
при
 если
если
 такое, что для любого разбиения
,
у которого
такое, что для любого разбиения
,
у которого
 ,
и для любого выбора промежуточных точек
выполняется неравенство
,
и для любого выбора промежуточных точек
выполняется неравенство
 .
.
Если
существует
 ,
то он называется двойным
интегралом
от функции
,
то он называется двойным
интегралом
от функции
 по множеству
и обозначается
по множеству
и обозначается
 или
или
 ,
а функция
называется интегрируемой на множестве
.
,
а функция
называется интегрируемой на множестве
.
Теорема 1.1 Функция, непрерывная на измеримом по Жордану компакте , интегрируема на этом компакте.
Теорема
1.2
Пусть функция
 ограничена на измеримом по Жордану
компакте
и множество ее точек разрыва имеет
жорданову меру нуль. Тогда функция
интегрируема на
.
ограничена на измеримом по Жордану
компакте
и множество ее точек разрыва имеет
жорданову меру нуль. Тогда функция
интегрируема на
.
Двойные интегралы обладают такими же свойствами, как и определенные интегралы (линейность, аддитивность, формулы среднего значения и т.п.).
Пример
1.1.
Вычислить интеграл
 ,
рассматривая его как предел интегральных
сумм при сеточном разбиении квадрата
на ячейки – квадраты со сторонами
длиной
,
рассматривая его как предел интегральных
сумм при сеточном разбиении квадрата
на ячейки – квадраты со сторонами
длиной
 и выбирая значение подынтегральной
функции в правых верхних вершинах этих
квадратов.
и выбирая значение подынтегральной
функции в правых верхних вершинах этих
квадратов.
∆ Разбиение
области интегрирования на ячейки
проводится прямыми
 ,
значение функции в правой верхней
вершине ячейки равно
,
значение функции в правой верхней
вершине ячейки равно
 .
Очевидно, что диаметр разбиения (диагональ
квадрата со стороной
)
.
Очевидно, что диаметр разбиения (диагональ
квадрата со стороной
)
 при
при
 .
Следовательно,
.
Следовательно,
 .
.
Учитывая,
что сумма первых
натуральных чисел равна
 ,
получим
,
получим  .
∆
.
∆
2.
Вычисление двойных интегралов с помощью
повторного интегрирования.
Пусть функция
определена в области
 ,
где
,
где
 - непрерывные функции на отрезке
- непрерывные функции на отрезке
 (рис. 1.1). Такую область
назовем элементарной
относительно оси
(рис. 1.1). Такую область
назовем элементарной
относительно оси
 (или
(или
 – трапециевидной).
– трапециевидной).
Теорема 1.3 Пусть:
1) существует двойной интеграл ;
2)
 существует определенный интеграл
существует определенный интеграл
 .
.
Тогда существует определенный интеграл


(он называется повторным) и справедливо равенство
 , (1.1)
, (1.1)
т.е. двойной интеграл равен повторному.








 y
y
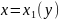









Рис.1.1 Рис. 1.2
Если
область
является элементарной
относительно оси
 (рис. 1.2), то при соответствующих условиях
справедлива формула, аналогичная (1.1):
(рис. 1.2), то при соответствующих условиях
справедлива формула, аналогичная (1.1):

 . (1.2)
. (1.2)
Область более сложного вида часто удается разбить на элементарные области, к которым применима формула (1.1) или (1.2) (рис 1.3).





Рис. 1.3
Пример
1.2
Свести двойной интеграл
к повторному двумя способами, если
- область, ограниченная кривыми
 .
.
∆ Область изображена на рис 1.4а).







 1
1
1
1



а) б)
Рис. 1.4
При
каждом значении
 переменная
изменяется от
переменная
изменяется от
 до
до
 ,
т.е. область
можно представить в виде
,
т.е. область
можно представить в виде
 .
По формуле (1.1) получаем
.
По формуле (1.1) получаем 
 .
.
Чтобы
воспользоваться формулой (1.2), надо
область
разбить на две части
 и
и
 ,
как показано на рис 1.4б). В области
переменная
меняется от -1 до 0, при каждом значении
переменная
изменяется от
,
как показано на рис 1.4б). В области
переменная
меняется от -1 до 0, при каждом значении
переменная
изменяется от
 до 1. В области
переменная
меняется от 0 до 1, при этом переменная
изменяется от
до 1. В области
переменная
меняется от 0 до 1, при этом переменная
изменяется от
 до 1. По формуле (1.2) получаем
до 1. По формуле (1.2) получаем



 .
∆
.
∆
Пример 1.3 Изменить порядок интегрирования в повторном интеграле
 .
.
∆ Область можно представить следующим образом (рис. 1.5).







Рис. 1.5
Если
переменная x
изменяется от
до
,
то
 ,
если меняется от
до
,
если меняется от
до
 ,
то
,
то
 .
Кривые
.
Кривые
 пересекаются в точке
пересекаются в точке
 .
Таким образом, переменная
меняется от
до
.
Найдем, в каких пределах меняется
переменная
.
Для этого разрешим выражения для
.
Таким образом, переменная
меняется от
до
.
Найдем, в каких пределах меняется
переменная
.
Для этого разрешим выражения для
 и
и
 относительно
:
относительно
:
 .
.
Применяя формулу (1.2), будем иметь:
 .
∆
.
∆
Пример
1.4 Вычислить
 ,
где
- треугольник, ограниченный прямыми
,
где
- треугольник, ограниченный прямыми
 .
.
∆ Треугольник изображен на рис. 1.6.







Рис. 1.6
Отрезком
 разделим
на два треугольника
и
,
элементарных относительно оси
.
Тогда
разделим
на два треугольника
и
,
элементарных относительно оси
.
Тогда
 .
По формуле (1.1) находим
.
По формуле (1.1) находим

=
 ,
,

=
 ;
;
следовательно,
 .
∆
.
∆
Пример
1.5
Вычислить
 ,
где
– задано неравенствами
,
где
– задано неравенствами
 .
.
∆ Область – неконцентричное кольцо - изображена на рис. 1.7.

3
Рис. 1.7
Обозначим
- круг
 ,
- круг
,
- круг
 .
Тогда
.
Тогда
 .
Продолжим функцию
.
Продолжим функцию
 с
на
,
полагая
для
с
на
,
полагая
для
 .
Тогда
.
Тогда
 .
.
Круги
и
зададим в виде
 .
По формуле (1.2) находим
.
По формуле (1.2) находим
 ,
,
так как функция во внутреннем интеграле нечетна.
 .
Следовательно,
.
Следовательно,
 .
∆
.
∆
Перемена порядка в повторном интеграле иногда существенно упрощает его вычисление.
Пример
1.6
Вычислить
 .
.
∆ Внутренний
интеграл не является элементарной
функцией
.
Изменим порядок интегрирования. Пределы
интегрирования в данном повторном
интеграле определяет треугольник (рис.
1.8), который можно задать и неравенствами
 .
.


Рис. 1.8
Следовательно,
 .
∆
.
∆
