Расчет частот нормального распределения
Частоты при нормальном распределении вариант рассчитываются по формуле, которая в общем случае имеет вид:
,
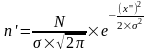где N – количество вариант в ряду;
- среднеквадратическое отклонение;
е – основание натурального логарифма;
x’’ – отклонение от среднего значения.
Для расчета частот нормального распределения разделим данную формулу на две части. В результате получаем:
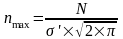- значение частоты,
которое принимает функция при нормированном
отклонении (отклонении от среднего
значения) равном нулю.
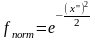- коэффициент,
учитывающий нормированное отклонение.
Расчет теоретических частот производим в форме таблицы. Для этого используем:
х’ – условные значения классов;
Условное значение класса определяется через условное среднее значение (см. расчет начальных моментов). Формула для определения условного значения класса:
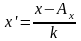
m1 – начальный момент первой степени;
x” – нормированное отклонение;
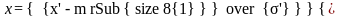
n’ – теоретические частоты для классов.
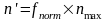
Таблица 7
Расчет теоретических частот нормального распределения
х |
х’ |
n |
nmax |
x’-m1 |
x” |
fnorm |
n’ |
8,25 |
-4 |
0 |
31,14737 |
-4,4863 |
-2,39909 |
0,056257 |
1,752 |
9,95 |
-3 |
6 |
-3,4863 |
-1,86433 |
0,175895 |
5,479 |
|
11,65 |
-2 |
18 |
-2,4863 |
-1,32957 |
0,413176 |
12,869 |
|
13,35 |
-1 |
22 |
-1,4863 |
-0,79481 |
0,729158 |
22,711 |
|
15,05 |
0 |
31 |
-0,4863 |
-0,26005 |
0,966751 |
30,112 |
|
16,75 |
1 |
25 |
0,513699 |
0,274705 |
0,962972 |
29,994 |
|
18,45 |
2 |
20 |
1,513699 |
0,809465 |
0,720639 |
22,446 |
|
20,15 |
3 |
17 |
2,513699 |
1,344224 |
0,405162 |
12,620 |
|
21,85 |
4 |
4 |
3,513699 |
1,878983 |
0,171137 |
5,330 |
|
23,55 |
5 |
3 |
4,513699 |
2,413743 |
0,054308 |
1,692 |
|
25,25 |
6 |
0 |
5,513699 |
2,948502 |
0,012948 |
0,403 |
|
|
|
146 |
|
|
|
|
145,408 |
Правильность расчетов подтверждается незначительным отклонением суммы теоретических частот от численности вариационного ряда.
Расчет функции нормального распределения целесообразно производить с использованием ЭВМ и электронных таблиц. Формула при этом будет иметь вид:
Для fnorm : =EXP(-1*(x”)^2/2)
Расчет теоретических частот распределения типа а
В том случае, если наблюдается некоторое отклонение графика от симметричного вида (значение асимметрии около 0,4 при критерии достоверности больше 2) рассчитывают распределение по типу А.
При этом используется функция нормального распределения, а также третья и четвертая производные от этой функции. Также в этой функции учитывается асимметрия и эксцесс:
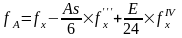
Функция нормального распределения рассчитывается как
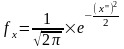
Третья производная от функции нормального распределения:
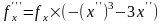
Четвертая производная от функции нормального распределения:
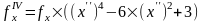
Отсюда функция распределения типа А принимает вид:
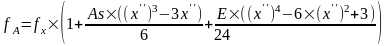
Частоты при распределении типа А вычисляются с учетом объема выборки и неполного среднеквадратического отклонения:
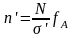
Независимо от того, подходит ли данный тип распределения к нашему примеру, сумма теоретических частот должна быть близкой к фактической численности вариационного ряда.
Для расчета распределения типа А при помощи электронных таблиц можно использовать следующие формулы:
Для функции нормального распределения:
=(1 / (2 * ПИ()) ^ 0,5) * EXP((-1) * (х”)^ 2 / 2)
Для третьей производной функции нормального распределения:
=(-1) * ((x”) ^ 3 - 3 * (x”)) * (f)
Для четвертой производной функции нормального распределения:
=((x”) ^ 4 - 6 *(x”) ^ 2 + 3) * (f)
В приведенных формулах вместо x” и f подставляются адреса ячеек, содержащих нормированное отклонение и функцию нормального распределения соответственно.
Таблица 8
Расчет теоретических частот для распределения типа А
х |
х` |
n |
x`-m1 |
x`` |
f |
f''' |
fIV |
|
|
fA |
n' |
8,25 |
-4 |
0 |
-4,4863 |
-2,39909 |
0,022443 |
0,148374 |
0,035765 |
-0,00481 |
-0,00086 |
0,016778 |
1,309 |
9,95 |
-3 |
6 |
-3,4863 |
-1,86433 |
0,070172 |
0,062237 |
-0,40515 |
-0,00202 |
0,009749 |
0,077905 |
6,082 |
11,65 |
-2 |
18 |
-2,4863 |
-1,32957 |
0,164833 |
-0,27005 |
-0,73872 |
0,008746 |
0,017775 |
0,191355 |
14,939 |
13,35 |
-1 |
22 |
-1,4863 |
-0,79481 |
0,290892 |
-0,54756 |
-0,11382 |
0,017733 |
0,002739 |
0,311364 |
24,309 |
15,05 |
0 |
31 |
-0,4863 |
-0,26005 |
0,385678 |
-0,29411 |
1,002302 |
0,009525 |
-0,02412 |
0,371085 |
28,972 |
16,75 |
1 |
25 |
0,513699 |
0,274705 |
0,38417 |
0,308637 |
0,980754 |
-0,01 |
-0,0236 |
0,350575 |
27,371 |
18,45 |
2 |
20 |
1,513699 |
0,809465 |
0,287494 |
0,545664 |
-0,14434 |
-0,01767 |
0,003473 |
0,273295 |
21,337 |
20,15 |
3 |
17 |
2,513699 |
1,344224 |
0,161636 |
0,259223 |
-0,73974 |
-0,0084 |
0,0178 |
0,171041 |
13,353 |
21,85 |
4 |
4 |
3,513699 |
1,878983 |
0,068274 |
-0,06807 |
-0,39042 |
0,002204 |
0,009394 |
0,079873 |
6,236 |
23,55 |
5 |
3 |
4,513699 |
2,413743 |
0,021666 |
-0,1478 |
0,043053 |
0,004787 |
-0,00104 |
0,025417 |
1,984 |
25,25 |
6 |
0 |
5,513699 |
2,948502 |
0,005165 |
-0,08672 |
0,136459 |
0,002808 |
-0,00328 |
0,00469 |
0,366 |
|
|
146 |
|
|
|
|
|
|
|
|
146,263 |
В этой таблице:
х – средние значения классов;
x’ – условные значения классов;
n – частоты;
x” – нормированное отклонение;
f – функция нормального распределения;
f’’’ и fIV – третья и четвертая производные функции нормального распределения соответственно;
fA – функция распределения типа А.