6.2. Спектры периодических сигналов

Периодический сигнал с частотой повторения и угловой частотой может быть представлен в виде ряда Фурье

, (6.7)

где – среднее значение за период, или постоянная составляющая сигнала; коэффициенты и называются соответственно амплитудами косинусоидальных и синусоидальных составляющих и вычисляются по формулам

, n=0,1,2,…, (6.8)

, n=1,2,….

Выражение (6.7) является суммой косинусоид и синусоид с частотами , что эквивалентно сумме только синусоид или космнусоид, но с различными фазами, например:

, (6.9)

Модуль амплитуды и фаза каждой гармоники определяется для (6.9) выражениями

; (6.10)

. (6.11)

Совокупность значений и называется спектром функции , определяется (6.7). Согласно (6.9) спектр периодического сигнала является линейчатым, или дискретным, состоящим из отдельных линий (гармоник), соответствующих частотам , , … (рис. 6.1). Для полной характеристики сигнала необходимо знать фазу каждой гармоники .

Рис. 6.1. Амплитудный спектр периодического сигнала

Вычисление коэффициентов и многие другие математические процедуры упрощаются при использовании вместо тригонометрических форм (6.7) и (6.9) комплексной записи ряда Фурье:

. (6.12)

Коэффициенты , называемые комплексными амплитудами, равны:

(6.13)

и связаны с , и выражениями

при n>0,

при n<0. (6.14)

Переход от комплексной формы к тригонометрической производят в конце анализа, используя формулы Эйлера

; ; (6.15a)

; . (6.15б)

6.2. Спектры непериодических сигналов

Непериодический сигнал может быть представлен в виде гармонических составляющих, частоты которых, однако, не являются дискретными, а пробегают непрерывную совокупность значений. Эта задача решается с помощью интегральных преобразований Фурье. Спектр сигнала может быть найден из соотношения

. (6.16)

Здесь называется спектральной плотностью сигнала, или спектральной характеристикой функции .

Обратное преобразование Фурье позволяет перейти от спектральной плотности к форме сигнала:

. (6.17)

Таким образом, с помощью преобразований Фурье сигналы любой формы могут быть представлены в виде совокупности гармонических составляющих с известными амплитудами и фазами, а сам гармонический сигнал становится как бы элементарным пробным сигналом при анализе цепей. Причем математические преобразования существенно упрощают, если гармонический сигнал, например напряжение

Представить в комплексной форме:

(6.18)

Если на каком-то участке линейной цепи действует гармоническая ЭДС, то на любом другом участке этой цепи может появиться только гармонический сигнал.

Комплексный коэффициент передачи

, (6.19)

где .

Если на выходе цепи с известным коэффициентом передачи действует произвольный сигнал , то сигнал на выходе цепи можно определить следующим образом: по (6.16) найти спектральную плотность , вычислить спектр сигнала на выходе цепи как

. (6.20)

И наконец, по (1.17) установить форму выходного сигнала

(6.21)

Коэффициент передачи остается под интегралом, так как зависит от частоты.

К сожалению, преобразование Фурье применимо только тогда, когда функция – абсолютно интегрируема. Для этого необходимо, чтобы интеграл сходился, т. е. был равен конечной величине. При невыполнении этого условия следует использовать иные способы преобразования.

Определим спектры некоторых наиболее распространенных сигналов.

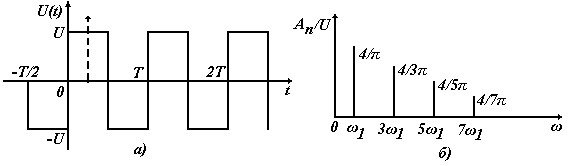
Рис. 6.2. Сигнал вида меандр (а) и его амплитудный спектр (б)

1. Периодическая последовательность колебаний прямоугольной формы (меандр) с амплитудой U (см. рис. 6.2а)

Согласно первому уравнению(6.8)

; .

В соответствии со вторым уравнением (6.8)

.

Учитывая, что , получаем

Подставляя эти значения коэффициентов в (6.7), запишем ряд Фурье

. (6.22)

Если отсчет времени начинать с середины импульса (на рис. 6.2а показано пунктиром), то и ряд Фурье принимает вид

. (6.23)

Из (6.22) и (5.23) видно, что меандр имеет линейчатый спектр (рис. 6.2б).

Заметим, что из-за наличия точек разрыва ряд Фурье с вычисленными коэффициентами не сходится при в этих точках к . Тем не менее при сумма ряда приближается к во всех остальных точках.

2. Одиночный импульс прямоугольной формы. В соответствии с (6.16) спектральная плотность импульса длительности и амплитуды U имеет вид (рис. 6.3б)

. (6.24)

Рис. 6.3. Прямоугольный импульс (а) и его спектральная плотность (б)

Воспользовавшись уравнениями Эйлера, получаем

(6.25)