1.3.4. Реакція Бєлоусова – Жаботинського

Брюсселятор є, звичайно, лише зручною моделлю нерівноважної системи. Але схожа поведінка спостерігається й у реальних системах, де протікають хімічні реакції автокаталітичного типу (наприклад, так звана реакція Бєлоусова - Жаботинського).

1.3.4.1. Історія досліджень та феноменологічний опис

Перші спостереження хімічних реакцій коливного типу належать ще до 1828 року (Г.Фехнер⁸, коливна електрохімічна реакція). Після цього коливання концентрацій реагентів та утворення просторово-періодичних структур у хімічних реакціях спостерігалися неодноразово, але не привертали особливої уваги та не знаходили раціонального пояснення аж до середини ХХ століття.

У 1951 році Б.П.Бєлоусов відкрив коливну хімічну реакцію в однорідному розчині – окислення лимонної кислоти броматом калію, причому в ролі каталізатора виступають іони та . У процесі цієї реакції розчин періодично змінює своє забарвлення – стає то безбарвним, то жовтим. Це пов’язано зі зміною концентрації іонів ^– та відношення концентрацій іонів (жовтий колір) та (безбарвні). Період коливань складає (в залежності від умов, у першу чергу – кислотності та температури) від 10 до 100 с. Коливання тривають приблизно протягом години і з часом згасають. Згасання пов’язане з тим, що система замкнена, і в неї не надходять речовини, необхідні для протікання реакції. Форма коливань може бути як квазігармонічною, так і суттєво несинусоїдальною (рис. 1.3.5 а-г). Інколи спостерігаються стохастичні коливання (рис. 1.3.5 д).

Якщо проводити реакцію в довгій тонкій трубці, розташованій вертикально, то можна спостерігати виникнення горизонтальних зон, що відповідають різним концентраціям реагентів. Вважається, що ці зони швидше всього виникають за рахунок зовнішніх градієнтів теиператури та густини. Коли реакція протікає в тонкому шарі рідини без перемішування (наприклад, у чашці Петрі), звичайно виникають концентричні хвилі з циліндричною симетрією (рис. 1.3.6) або спіральні хвилі, що обертаються (рис.1.3.7). Ці структури вперше спостерігав у 1974 році А.Т.Вінфрі⁹ (США). Можливі й інші варіанти поведінки.

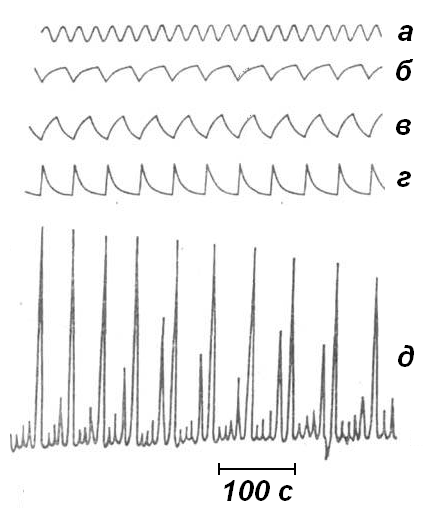
Рис. 1.3.5. Коливання концентрації іонів Се4+ у реакції Бєлоусова - Жаботинського: а – гармонічні коливання; б-г – пилкоподібні коливання; д – стохастичні коливання.

Рис. 1.3.6. Провідні центри в тонкому шарі рідини з реакцією Бєлоусова - Жаботинського. Інтервал між кадрами – 30 с.

Статтю Бєлоусова з описом цієї реакції двічі відхиляли редакції академічних хімічних журналів, і вона була надрукована лише в 1958 році у вузьковідомчому збірнику. Неприйняття робіт Бєлоусова пов’язане з тим, що, на думку більшості тогочасних дослідників, вони суперечили другому початку термодинаміки, як його тоді розуміли. Коли ж у середині 1950х років з’явилися роботи І.Р.Пригожина з нерівноважної термодинаміки, які, зокрема, передбачали можливість хімічних реакцій коливного типу в системах, далеких від термодинамічної рівноваги, інтерес до робіт Бєлоусова стрімко зріс.

Пізніше (з 1961 року) дослідження коливних хімічних реакцій продовжив А.М.Жаботинський. Саме за його провідної участі було з’ясовано механізм реакції. Він же запропонував інші варіанти окислювачів та каталізаторів, які давали ефектніші кольори (фіалково-червоний – яскраво синій).

В загальному вигляді реакцію Бєлоусова - Жаботинського можна уявити собі як набір двох частин – окислення іонів церію, , та їх наступного відновлення, . Обидві ці реакції відбуваються в присутності каталізаторів та окислювачів. Серед проміжних реакцій є й автокаталітичні. Але питання про те, які саме речовини забезпечують автокаталіз, досі залишається нез’ясованим. Це пов’язано зі складністю реальної системи, яка містить не один десяток проміжних компонентів. Тому було запропоновано ряд спрощених моделей, які дають якісно подібний результат. Однією з таких моделей є запропонована Р.Філдом¹⁰, Е.Кересом¹¹ та Р.Нойесом¹² (1972) модель орегонатора¹³.

Рис. 1.3.7. Багаторукавні спіральні хвилі в тонкому шарі рідини з реакцією Бєлоусова - Жаботинського. Інтервал між кадрами – 15 с.

1.3.4.2. Рівняння орегонатора

Модель орегонатора включає такі хімічні реакції:

;

;

; (1.3.35)

;

.

Третя з реакцій (1.3.35) включає окислення іону церію бромнуватою кислотою , п’ята – відновлення іону . До того ж, третя з реакцій (1.3.31) належить до автокаталітичного типу – виробництво бромистої кислоти пропорційне її початковій концентрації.

Позначимо концентрації через , – через , – через , – через , – через , – через . За змістом задачі всі ці величини мають бути невід’ємними. Тоді, нехтуючи несуттєвими компонентами, систему реакцій (1.3.35) можна переписати у формі:

;

;

; (1.3.36)

;

.

Вважатимемо величини , та сталими, а , , – змінними. Тоді на основі (1.3.36) для них можна записати такі кінетичні рівняння:

;

; (1.3.37)

(для спрощення в двох останніх рівняннях у правих частинах степеневі залежності від замінено на лінійні). Рівняння (1.3.37) якраз і відповідають моделі орегонатора.

Рівняння (1.3.37) записано в припущенні, що в системі має місце перемішування, так що концентрації всіх компонент не залежать від координат. В дійсності ж так буває не завжди, й тоді треба брати до уваги процеси дифузії. З урахуванням дифузії система (1.3.37) набуває вигляду:

;

; (1.3.38)

.

1.3.4.3. Динаміка орегонатора

Обговоримо поведінку орегонатора за наявності перемішування.

Перейшовши до безрозмірних змінних

, , , , (1.3.39)

, , ,

рівняння орегонатора (1.3.37) можна переписати у формі:

;

; (1.3.37 а)

.

Для стаціонарного стану системи (1.3.37 а) легко отримати рівняння

, , . (1.3.40)

З трьох коренів системи (1.3.40) фізичний зміст має лише один –

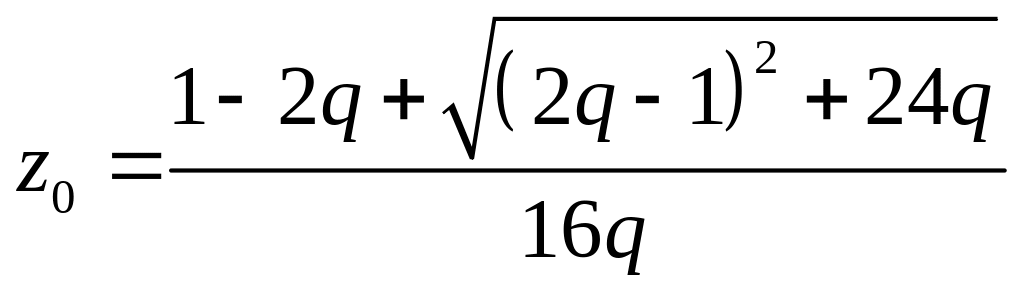(1.3.40 а)

( та визначаються через за формулами (1.3.40)).

Якщо лінеаризувати систему (1.3.37 а) по малих відхиленнях від стаціонарного стану (1.3.40 а), а потім підставити для всіх змінних розв’язок у формі , неважко отримати характеристичне рівняння для у формі

, (1.3.41)

де

, ,

. (1.3.42)

Відповідно до критерію Рауса¹⁴ - Гурвіца¹⁵, всі корені мають від’ємні дійсні частини за одночасного виконання умов

, . (1.3.43)

Очевидно, при варіюванні параметрів моделі , та в діапазоні від нуля до нескінченності обов’язково знайдеться область, де хоча б одна з умов (1.3.43) порушиться. В цій області положення стаціонарної рівноваги втратить стійкість (пор. з пп. 1.3.3.2-1.3.3.3).

Реально система рівнянь (1.3.37 а) розв’язується числовими методами і в деякій області значень параметрів справді має розв’язки типу релаксаційних автоколивань.

Система (1.3.37 а) має півтора ступені вільності. Отже, в принципі вона може описувати не тільки регулярні коливання, але й стохастичний режим. Такий режим, як уже вказувалося, справді спостерігається в реакціях Бєлоусова – Жаботинського.

В загальному випадку, тобто за наявності дифузії, орегонатор може в залежності від значень параметрів відповідати середовищам із відновленням або середовищам автоколивного типу (див. нижче пп. 2.2.2 - 2.2.3).