1.3.3. Брюсселятор
Одним із широко відомих модельних об’єктів нерівноважної термодинаміки є так званий брюсселятор – реактор, у якому протікає деяка реакція автокаталітичного типу. Він був запропонований І.Р.Пригожиним зі співробітниками і названий на честь Брюсселя – міста, де Пригожін працював більшу частину життя і де він створив всесвітньо відому школу з нерівноважної термодинаміки.
1.3.3.1. Опис моделі та вихідні рівняння
Розглянемо деяку модельну хімічну реакцію, відому в літературі як брюсселятор:
![]() ;
;
![]() ;
;
![]() ; (1.3.22)
; (1.3.22)
![]() .
.
Вважатимемо, що концентрації початкових
речовин
![]() та продуктів реакції
та продуктів реакції
![]() підтримуються сталими, тоді як концентрації
проміжних продуктів
підтримуються сталими, тоді як концентрації
проміжних продуктів
![]() можуть змінюватися з часом. Тоді,
позначивши концентрації тими ж літерами,
що й хімічні речовини, і вважаючи, що
всі константи швидкостей реакцій
дорівнюють одиниці, можна записати (для
одновимірної моделі з урахуванням
дифузії) кінетичні рівняння для
концентрацій проміжних продуктів
реакції в такому вигляді:
можуть змінюватися з часом. Тоді,
позначивши концентрації тими ж літерами,
що й хімічні речовини, і вважаючи, що
всі константи швидкостей реакцій
дорівнюють одиниці, можна записати (для
одновимірної моделі з урахуванням
дифузії) кінетичні рівняння для
концентрацій проміжних продуктів
реакції в такому вигляді:
 (1.3.23)
(1.3.23)
Ще раз підкреслимо, що в брюсселяторі концентрації початкових речовин та продуктів реакції підтримуються сталими. Це означає, як уже неодноразово вказувалося, що речовини весь час відбираються від системи, а речовини , навпаки, постійно вводяться ззовні. Таким чином, розглянута система є відкритою. Наявність потоків речовини означає, що в системі будуть існувати й потоки ентропії. У випадку утворення структур (див. нижче) такий потік, очевидно, має бути спрямованим назовні.
1.3.3.2. Стаціонарний однорідний стан та його стійкість
Стаціонарний однорідний стан системи відповідає термодинамічній гілці. Для нього
 (1.3.24)
(1.3.24)
звідки
![]() ,
, ![]() . (1.3.25)
. (1.3.25)
Можна було б, як це робилося вище, підрахувати надлишкове виробництво ентропії і дослідити його знак. Але, як уже згадувалося, негативне надлишкове виробництво ентропії є лише необхідною, але не достатньою умовою порушення стійкості стану рівноваги. Тому ми підемо більш прямолінійним шляхом – безпосередньо проаналізуємо стійкість стаціонарного однорідного розв’язку (1.3.25) системи (1.3.23).
Для того, щоб з’ясувати стійкість розв’язку (1.3.25), розглянемо малі відхилення від нього:
![]() ,
, ![]() ,
, ![]() . (1.3.26)
. (1.3.26)
Тоді з (1.3.23) можна отримати:
 (1.3.27)
(1.3.27)
Оскільки рівняння (1.3.27) лінійні, їхній розв’язок можна шукати у формі експонент:
![]() . (1.3.28)
. (1.3.28)
Підставивши (1.3.28) до (1.3.27), можна отримати систему лінійних однорідних алгебраїчних рівнянь щодо амплітуд відхилень:
 (1.3.29)
(1.3.29)
Прирівнявши до нуля визначник системи
(1.3.29), отримаємо квадратне рівняння щодо
![]() .
Його корені можна подати у формі
.
Його корені можна подати у формі
![]() , (1.3.30)
, (1.3.30)
![]() ,
, ![]() .
.
Зрозуміло, що стаціонарний однорідний
розв’язок (1.3.26) системи (1.3.23) буде стійким
щодо збурення із заданим значенням
![]() лише за виконання умови
лише за виконання умови
![]() .
.
1.3.3.3. Характерні області стійкості-нестійкості та переходи між ними
Розіб’ємо площину
![]() на характерні області з різними значеннями
на характерні області з різними значеннями
![]() та
та
![]() (рис. 1.3.2).
(рис. 1.3.2).
В області І маємо
![]() (
(![]() ).
Тут малі відхилення від розв’язку
(1.3.25) будуть експоненціально згасати з
часом.
).
Тут малі відхилення від розв’язку
(1.3.25) будуть експоненціально згасати з
часом.
В області ІІ маємо
![]() ,
.
Тут згасання малих відхилень від
однорідного стаціонарного розв’язку
матиме осциляторний характер.
,
.
Тут згасання малих відхилень від
однорідного стаціонарного розв’язку
матиме осциляторний характер.
Отже, І і ІІ – це області стійкості однорідного стаціонарного розв’язку. В усіх інших областях цей розв’язок буде нестійким.
|
Рис. 1.3.2. Характерні області стійкості та нестійкості стаціонарного однорідного розв’язку для брюсселятора. Області І, ІІ є стійкими, області ІІІ-V нестійкими. |
В області ІІІ маємо
,
![]() .
Іншими словами, в цій області відхилення
від положення рівноваги матиме характер
біжучої хвилі, амплітуда якої з часом
зростає, або суперпозиції таких хвиль.
Випадок
.
Іншими словами, в цій області відхилення
від положення рівноваги матиме характер
біжучої хвилі, амплітуда якої з часом
зростає, або суперпозиції таких хвиль.
Випадок
![]() (або
(або
![]() )
дає синфазні коливання, амплітуда яких
зростає з часом. Перехід з області II в
область III відповідає (при
)
відомій біфуркації Андронова4
– Хопфа5,
або м’якому самозбудженню коливань.
)
дає синфазні коливання, амплітуда яких
зростає з часом. Перехід з області II в
область III відповідає (при
)
відомій біфуркації Андронова4
– Хопфа5,
або м’якому самозбудженню коливань.
В області IV маємо
,
![]() .
Відхилення від положення рівноваги
являє собою просторово періодичне
збурення, що монотонно зростає з часом
(так звана аперіодична нестійкість),
або набір таких збурень.
.
Відхилення від положення рівноваги
являє собою просторово періодичне
збурення, що монотонно зростає з часом
(так звана аперіодична нестійкість),
або набір таких збурень.
Нарешті, в області V буде
,
![]() ,
тобто поведінка відхилень від рівноваги
буде приблизно такою самою, як і в області
ІV. Перехід з області І в область V
відповідає так званій біфуркації
Тюрінга.
,
тобто поведінка відхилень від рівноваги
буде приблизно такою самою, як і в області
ІV. Перехід з області І в область V
відповідає так званій біфуркації
Тюрінга.
1.3.3.4. Зведення рівнянь брюсселятора до узагальненого рівняння Релея
Проведений аналіз поведінки відхилень брюсселятора від однорідного стаціонарного стану стосується (за наявності нестійкості) лише початкових моментів часу, поки відхилення залишаються малими.
Покажемо, що в частинному випадку просторово однорідної системи (що може бути досягнуто, наприклад, штучним перемішуванням реагентів) система рівнянь (1.3.23) може бути зведена до узагальненого рівняння Релея6.
Справді, якщо система є просторово однорідною, просторові похідні в рівняннях (1.3.23) зникають, і ця система перетворюється на систему рівнянь у повних похідних:
 (1.3.23 а)
(1.3.23 а)
Перейдемо від змінних
до нових змінних
![]() (повна концентрація реагентів) та
(повна концентрація реагентів) та
![]() .
Заміни
.
Заміни
![]() та
та
![]() в першому рівнянні системи (1.3.23 а)
надають йому вигляду
в першому рівнянні системи (1.3.23 а)
надають йому вигляду
![]() . (1.3.31)
. (1.3.31)
Додавання рівнянь (1.3.23 а) дає в нових змінних:
![]() . (1.3.32)
. (1.3.32)
Система (1.3.31)-(1.3.32) має стаціонарні точки
![]() ,
,
![]() .
У змінних
.
У змінних
![]() ,
,
![]() вона набуває вигляду
вона набуває вигляду
 (1.3.33)
(1.3.33)
Систему (1.3.33) легко звести до одного
рівняння щодо змінної
![]() :
:
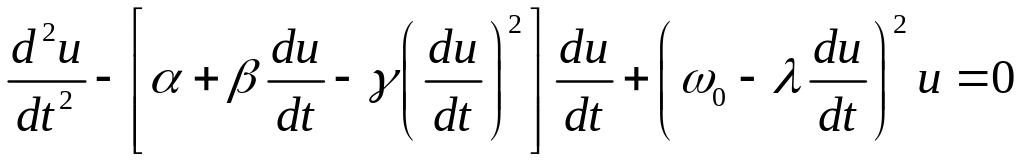 , (1.3.34)
, (1.3.34)
де використані позначення
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
При
![]() та
та
![]() рівняння (1.3.34) зводиться до відомого
рівняння Релея, що описує, зокрема,
автоколивання автогенератора
Ван-дер-Поля7.
Доданок, пропорційний параметру
рівняння (1.3.34) зводиться до відомого
рівняння Релея, що описує, зокрема,
автоколивання автогенератора
Ван-дер-Поля7.
Доданок, пропорційний параметру
![]() ,
відповідає врахуванню квадратичної
нелінійності прохідної характеристики
активного елемента (лампи або транзистора).
В режимі квазігармонічних коливань,
коли їхню амплітуду в певному сенсі
можна вважати малою, він взагалі не
впливає на основну гармоніку коливань,
але приводить до появи другої гармоніки
в спектрі коливань. В режимі релаксаційних
коливань він впливає на форму граничного
циклу. Доданок, пропорційний
,
описує ефект неізохронності
вплив амплітуди коливань на їхню частоту.
,
відповідає врахуванню квадратичної
нелінійності прохідної характеристики
активного елемента (лампи або транзистора).
В режимі квазігармонічних коливань,
коли їхню амплітуду в певному сенсі
можна вважати малою, він взагалі не
впливає на основну гармоніку коливань,
але приводить до появи другої гармоніки
в спектрі коливань. В режимі релаксаційних
коливань він впливає на форму граничного
циклу. Доданок, пропорційний
,
описує ефект неізохронності
вплив амплітуди коливань на їхню частоту.
Як випливає з рівняння (1.3.34), збудження
автоколивань можливе за умови
![]() .
Легко переконатись у тому, що ця умова
для просторово однорідних розв’язків
(
)
відповідає областям ІІІ-ІV
на рис.1.3.2 (в аналізованому випадку
.
Легко переконатись у тому, що ця умова
для просторово однорідних розв’язків
(
)
відповідає областям ІІІ-ІV
на рис.1.3.2 (в аналізованому випадку
![]() ).
).
Таким чином, у брюсселяторі з перемішуванням за певних значень параметрів можуть виникати і встановлюватися періодичні автоколивання.
1.3.3.5. Нелінійна стадія динаміки брюсселятора
Крім найпростіших автоколивань, у брюсселяторі на нелінійній стадії його динаміки можуть виникати й інші типи стаціонарних та динамічних дисипативних структур.
Для дослідження поведінки брюсселятора в пізні моменти часу можна скористатися відомими наближеними методами розв’язання нелінійних рівнянь. Це, зокрема, вдається зробити, якщо форма коливань (у часі) або форма структури (в просторі) близька до гармонічної. Але найбільш зручно досліджувати нелінійну стадію нестійкості числовими методами.
В залежності від параметрів моделі А, В структури, що виникають у брюсселяторі, характеризуються дуже великою різноманітністю. Крім того, вони суттєво залежить від граничних умов. Так, у найпростіших одновимірних випадках граничні умови можуть, наприклад, дискретизувати спектр можливих значень .
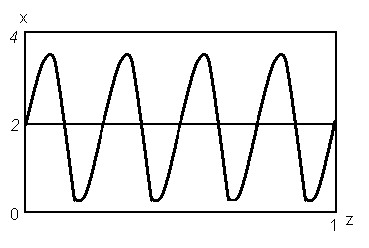
При k=0 (точніше, при Dx=Dy=0) в області ІІІ система, як було щойно показано (п.1.3.3.4), поводить себе як розподілений автогенератор – відбуваються синфазні коливання в усьому просторі. При k0 може спостерігатися щось схоже на стоячу хвилю (рис. 1.3.3).
|
|
|
|
|
t=3.435 |
Рис. 1.3.3. Часова еволюція розподілу X(z) в одновимірному брюсселяторі при L=1, Dx=810-3, Dy=410-3, A=2, B=5.45. |
||
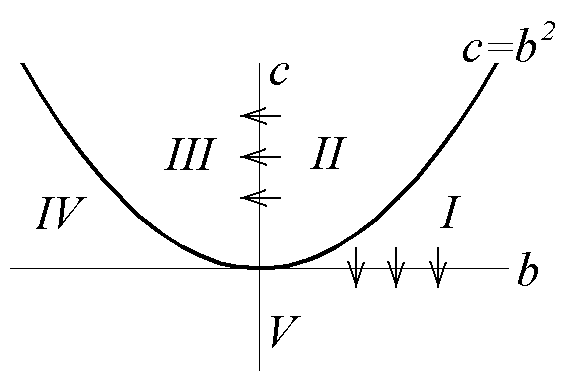
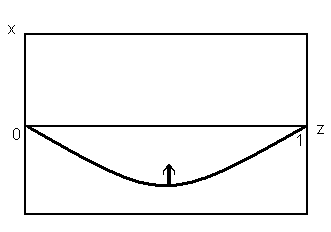
В областях IV-V можливе утворення
стаціонарних просторово-періодичних
структур (рис. 1.3.4). Такі структури можуть
виникати лише при достатньо великих
значеннях параметра
![]() (
(![]() – довжина системи).
– довжина системи).
|
Рис. 1.3.4. Стаціонарна структура X(z) в одновимірному брюсселяторі при L=1, DX=1.610-3, DY=810-3, A=2, B=4.47). |
Кількість та складність можливих структур у брюсселяторі різко зростає при переході до дво- та тривимірних моделей.

 t=0
t=0 t=0.68
t=0.68 t=1.10
t=1.10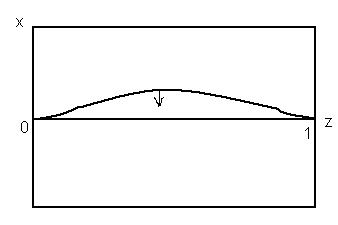 t=1.88
t=1.88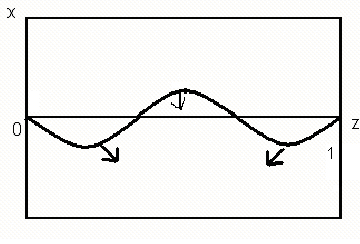 t=2.04
t=2.04