2.Модель гармонического осциллятора

Для наглядности будем рассматривать простейший случай – колебание двухатомной молекулы, для определенности выберем молекулу хлористого водорода HCl. Решение любой задачи подразумевает выбор некоторой модели, по возможности более простой, но отражающей основные свойства реальной системы. Определимся с моделью двухатомной молекулы, объясняющей инфракрасные колебательные спектры поглощения.

В начале будем исходить из максимально упрощенной модели. Очевидно, таковой является система из двух материальных точек с массами, равными массам ядер молекулы, и противоположными зарядами. В случае молекул, состоящих из одинаковых атомов, например H₂, материальные точки нашей модели не имеют заряда. В случае же молекулы HCl, точка, соответствующая водороду, имеет отрицательный заряд, а точка, соответствующая хлору – положительный. В данном приближении дипольный момент d молекулы линейно зависит от расстояния между ядрами. Далее, предположим, что потенциал взаимодействия ядер строго гармонический, т.е. потенциальная энергия пропорциональна квадрату отклонения расстояния между ядрами R от равновесного расстояния R_e: . Здесь – коэффициент жесткости связи ядер. В дальнейшем отклонение будем обозначать как r.

Как известно, задачу колебания двух материальных точек с массами m₁ и m₂ можно свести к задаче колебания одной точки с массой 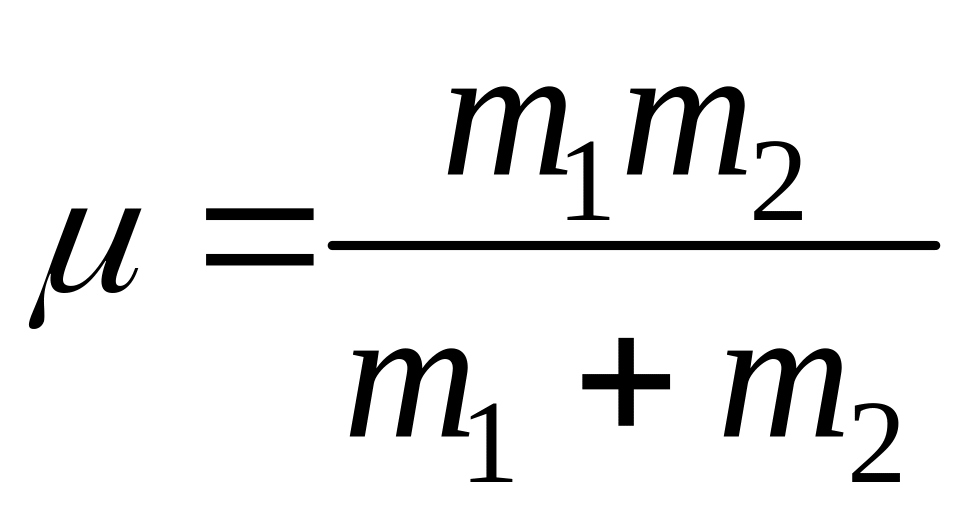. Масса называется приведенной. Тогда частота колебаний ядер в нашей модели равна 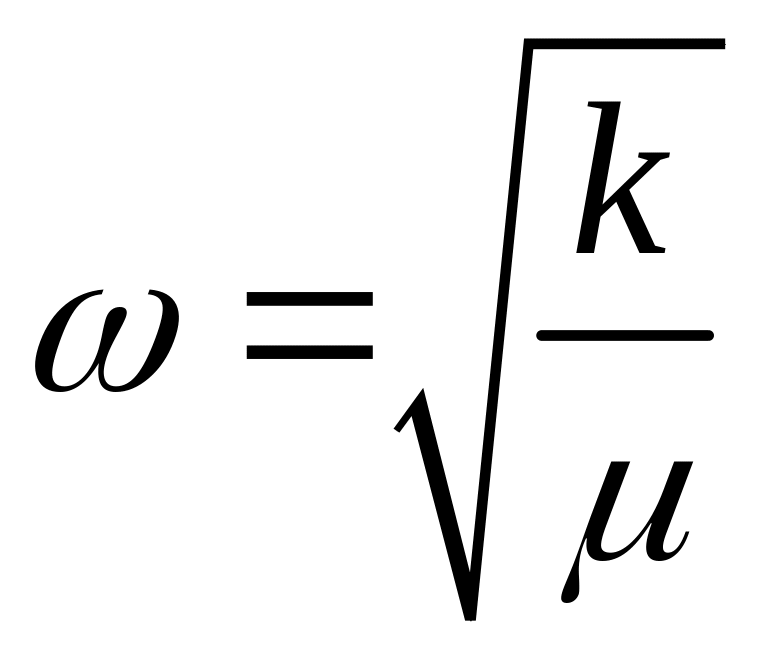. Теперь становится ясным, что простейшей моделью двухатомной молекулы как колебательной системы, является одномерный гармонический осциллятор.

Для гармонического осциллятора имеется точное решение уравнения Шредингера: известны и волновые функции и соответствующие им значения энергии. Именно, энергетический спектр (набор разрешенных энергий) одномерного гармонического осциллятора задается выражением

,

Естественно этой же формулой задается и энергетический спектр двухатомной молекулы в гармоническом приближении.

Здесь уместно сделать замечание относительно размерностей используемых физических величин. В спектроскопии часто используется частота (иначе, волновое число), по определению она равна отношению . Частота имеет размерность длины в минус первой степени. Как правило, в литературе используется единица измерения см^-1, реже применяется м^-1. Кроме того, часто формально заменяется на , благодаря чему энергия также принимает размерность см^-1. Энергия гармонического осциллятора тогда запишется как

.

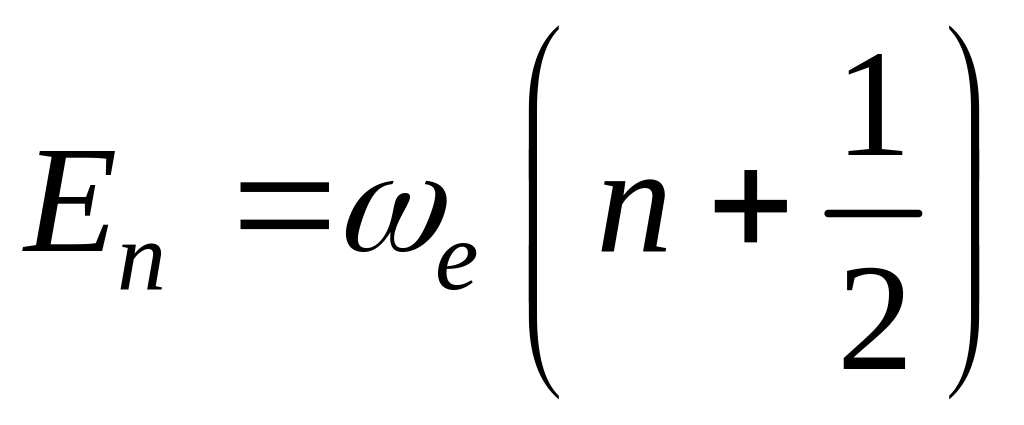Можно легко показать (см. раздел 2.1), что в рамках нашей модели поглощение и испускание электромагнитного излучения двухатомными молекулами, состоящими из одинаковых атомов (дипольный момент которых равен нулю) невозможно. Для модели молекул, состоящих из различных атомов (дипольный момент отличен от нуля), существует правило отбора n=+1, т.е. с n‑го уровня она может перейти лишь на n-1-й уровень (испуская при этом квант электромагнитного излучения) либо на n+1-й (поглощая квант). Это означает, что если бы данная модель совершенно точно описывала реальную молекулу, то в колебательном спектре поглощения двухатомных молекул была бы лишь одна линия с частотой , соответствующей разности энергий двух соседних линий:

.

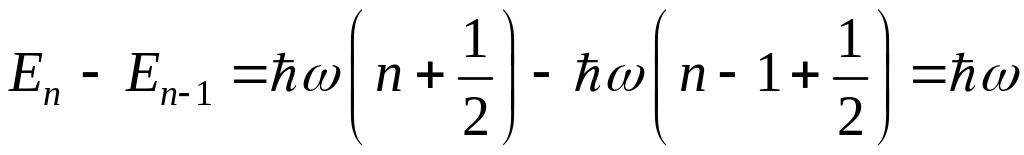В действительности же молекулы, не имеющие дипольного момента, могут поглощать и испускать излучение за счет отличных от нуля

4 мультипольных моментов: квадрупольного, октупольного, гексадекапольного и т.д. моментов. Обычно интенсивность взаимодействия таких молекул с излучением очень низка, и мы не будем рассматривать этот случай здесь.

Как показывает детальный расчет, для молекул, состоящих из различных атомов, вклад квадрупольного и последующих моментов оказывается пренебрежимо малым, поэтому в дальнейшем мы будем считать, что молекулы имеют только дипольный момент.

В спектрах поглощения реальных молекул, состоящих из разных атомов, помимо интенсивной линии основного тона, имеющей частоту примерно равную  (переход 0→1), имеются и гораздо более слабые линии обертонов с частотами приблизительно 2, 3, … (переходы 0→2, 0→3, …). Таким образом, наша простейшая модель описывает реальную молекулу лишь приближенно. Для более точного описания спектров необходимо усложнить нашу модель - ввести понятие ангармоничности.

Обсуждая ангармоничность колебаний молекул, следует отметить, что существует механическая ангармоничность и электрооптическая ангармоничность.

Механическая ангармоничность связана с отличием потенциала взаимодействия ядер молекулы от строго гармонического. Как известно, потенциальная функция реальных молекул имеет минимум при r=0 (равновесное расстояние между ядрами), стремится к бесконечности при стремлении r к 0 (возрастание силы отталкивания при сближении ядер на малое расстояние) и стремится к некоторой постоянной величине при стремлении r к бесконечности. Формально механическая ангармоничность описывается введением разложения потенциальной функции по колебательной координате r:

Коэффициенты будем называть параметрами механической ангармоничности. При обращении в нуль данных коэффициентов потенциал обращается в гармонический.

Механическая ангармоничность приводит к смещению энергетических уровней молекулы от уровней гармонического осциллятора . Зависимость энергетических уровней молекулы E_n от квантового числа n принято записывать в виде ряда по степеням числа :

(1.1)

Безразмерные коэффициенты не равны нулю лишь для ангармонических колебаний и поэтому называются параметрами ангармоничности. Перед определен знак минус, потому что для всех молекул данное слагаемое дает отрицательный вклад в энергию и тогда оказывается положительным, что удобно при вычислениях. Величины параметров ангармоничности быстро убывают с возрастанием номера соответствующего слагаемого: <<1, << …

Электрооптическая ангармоничность связана с нелинейной зависимостью дипольного момента молекулы от расстояния между ядрами. Данный факт определяется перераспределением электронной плотности в молекуле при изменении межъядерного расстояния. В общем случае, дипольный момент следует записывать в виде степенного разложения по колебательной координате.

Учет механической и электрооптической ангармоничностей позволяет объяснить переходы с n≠+1 (обертоны). Следует отметить, что данные переходы объясняются уже при учете хотя бы только одного вида ангармоничности (механической либо электрооптической). В действительности оба вида ангармоничности дают свой вклад в появление обертонов и в их относительные интенсивности (подробнее см. в 3.4).

Наблюдаемые линии в спектрах поглощения соответствуют переходам с основного уровня, так как основной уровень самый заселенный и вероятность данных переходов при поглощении гораздо выше, чем переходов с остальных уровней. При переходе 0→n поглощаются фотоны с энергией, равной разности энергий n–го и основного энергетических уровней:

Если в эксперименте мы можем измерить лишь частоту одной линии, то, разумеется, этого недостаточно, чтобы установить чему равны параметры ангармоничности. По этим данным можно лишь примерно судить о величине частоты , которую в этом случае можем положить равной экспериментальной частоте. Если наблюдаются две линии, то можно найти гармоническую частоту и параметр , так как теперь мы имеем два уравнения. Аналогичным образом по трем экспериментальным частотам мы можем найти и параметры и . Заметим, что значение вновь найденной частоты будет несколько отличаться от предыдущей. Тоже справедливо и для . И так далее – чем больше мы имеем экспериментальных частот, тем больше параметров ангармоничности мы можем найти и тем точнее описать потенциал реальной молекулы.