§ 38.Скалярное произведение двух векторов

Скалярным произведением 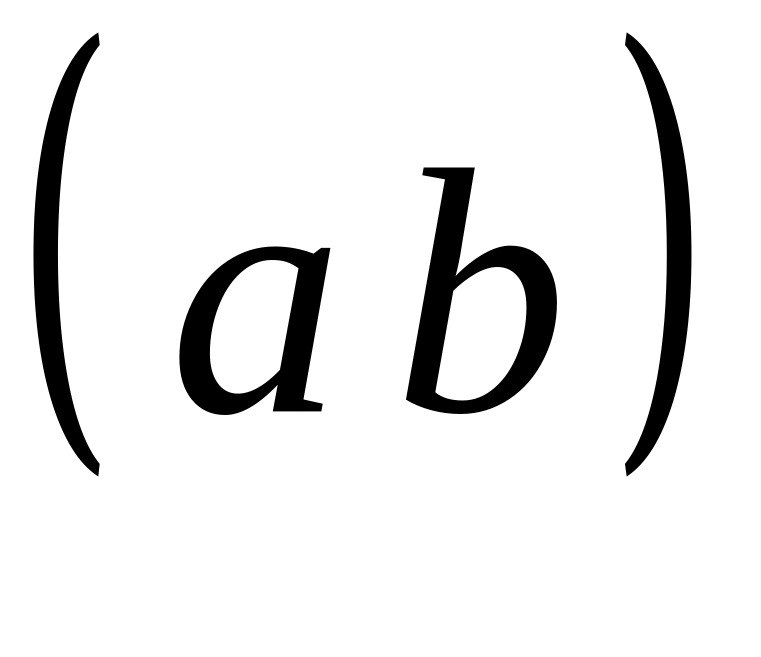двух векторов и в случае, если векторы ненулевые, называется произведение их модулей на косинус угла между ними.

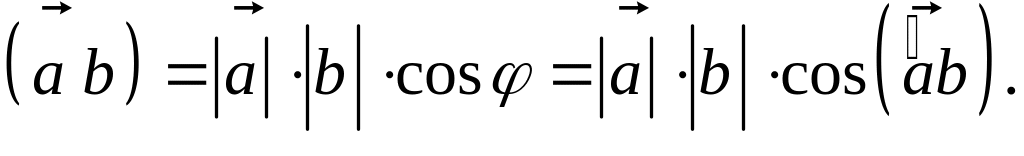
Если ненулевые векторы и коллинеарны и направлены в одну сторону, то угол между ними считается равным нулю, а если ненулевые векторы и коллинеарны, но имеют противоположное направление, то угол между ними считается равным .

Наконец, если ; или (или ), то скалярное произведение 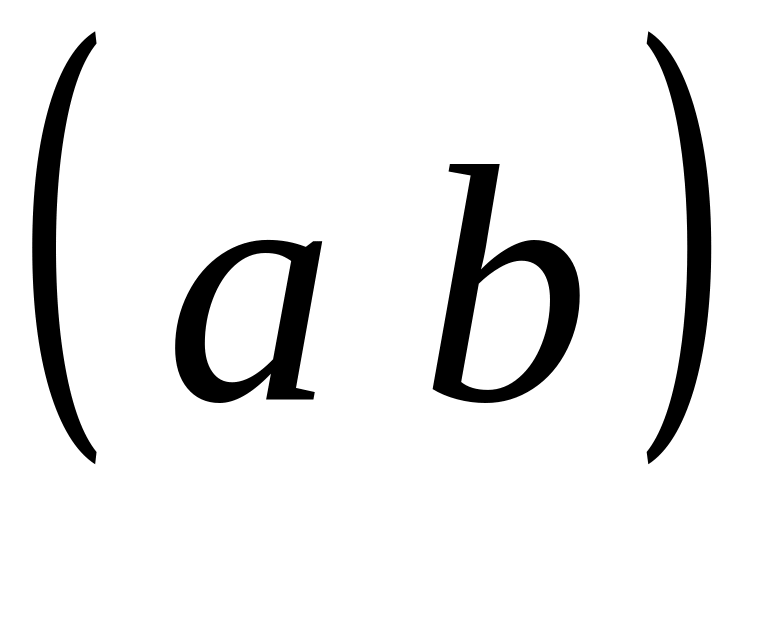по определению считается равным нулю.

Из этого определения следует, что скалярный квадрат вектора , т.е. скалярное произведение равно квадрату модуля вектора .

В самом деле .

Отсюда 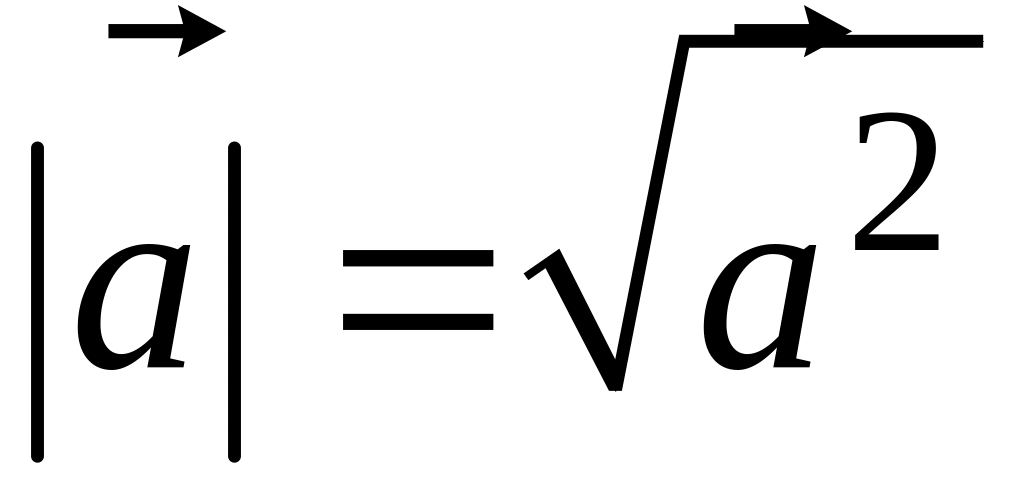, то есть модуль вектора равен квадратному корню из его скалярного квадрата.

Скалярное произведение двух векторов обладает следующими свойствами:

1) коммутативность;

2) (ассоциативность относительно умножения на число);

3) (дистрибутивность относительно сложения).

Свойство 1) сразу следует из определения скалярного произведения.

Для доказательства свойств 2) и 3) заметим, что в силу теоремы 4 § 11 имеем.

(Теорема 4 § 11 состояла в следующем. Координата ортогональной проекции вектора на ось l равна длине АВ этого вектора, умноженной на косинус угла между вектором и осью l: .)

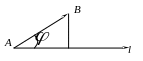
Итак, согласно теореме 4 § 11 имеем

.

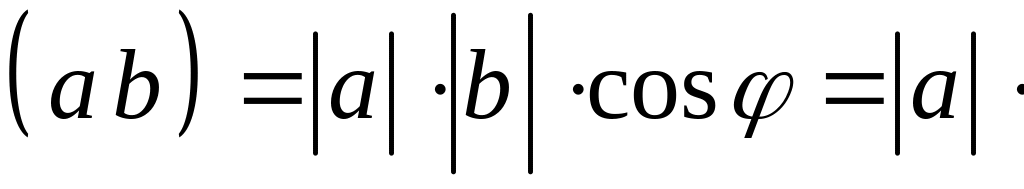
Доказательство свойства 2): Имеем:

=

.

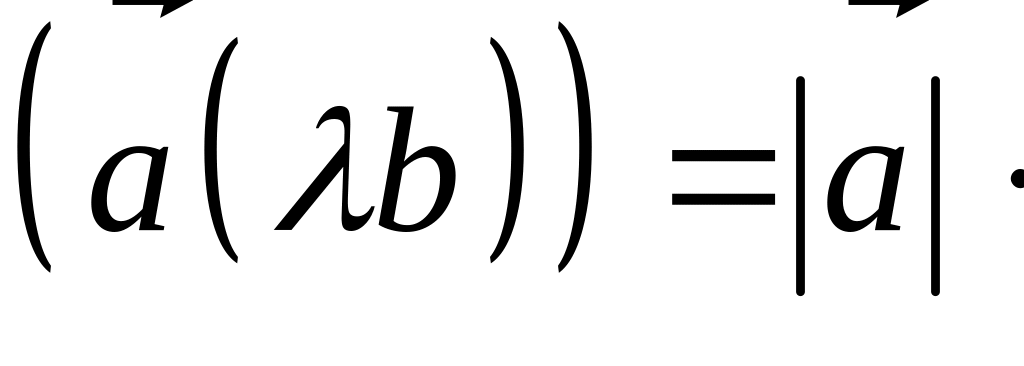
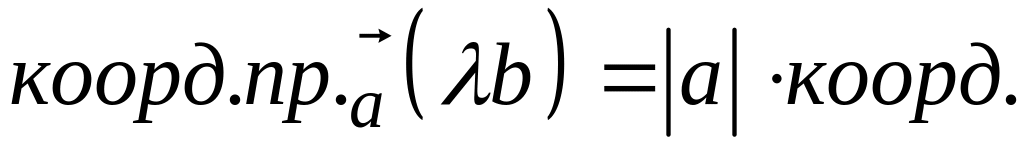
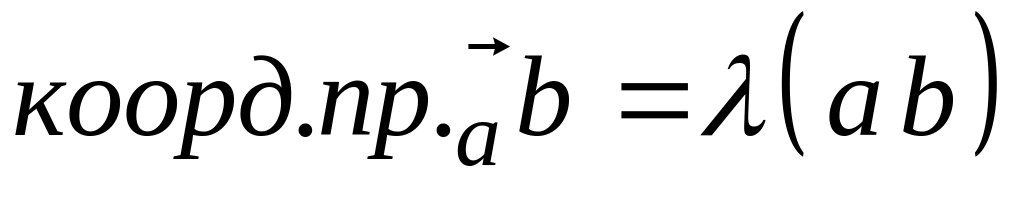Доказательство свойства 3):

( )=

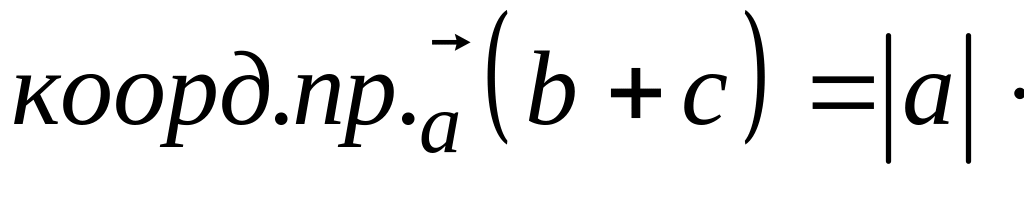
= коорд.пр. коорд.пр. = .

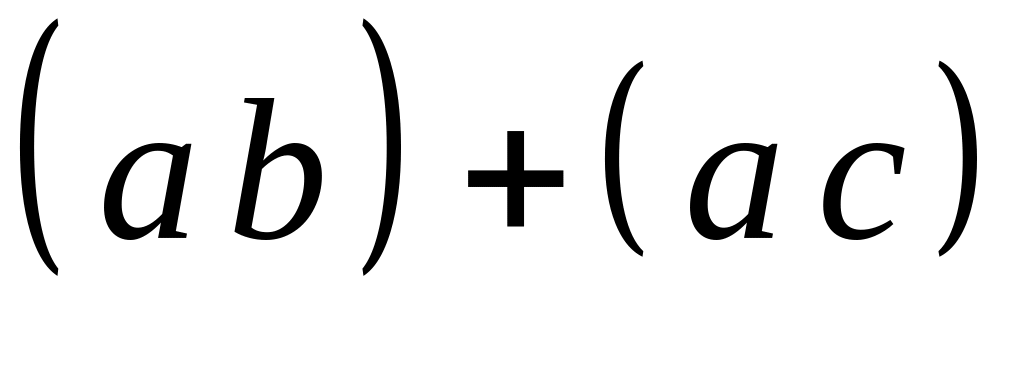§ 39. Выражение скалярного произведения в координатах

Ортонормированным базисом называется упорядоченная тройка единичных и попарно ортогональных векторов.

Пусть относительно ортонормированного базиса заданы два вектора своими координатами:

; ,

то есть ; .

На основании свойств 1) – 3) скалярного произведения; находим

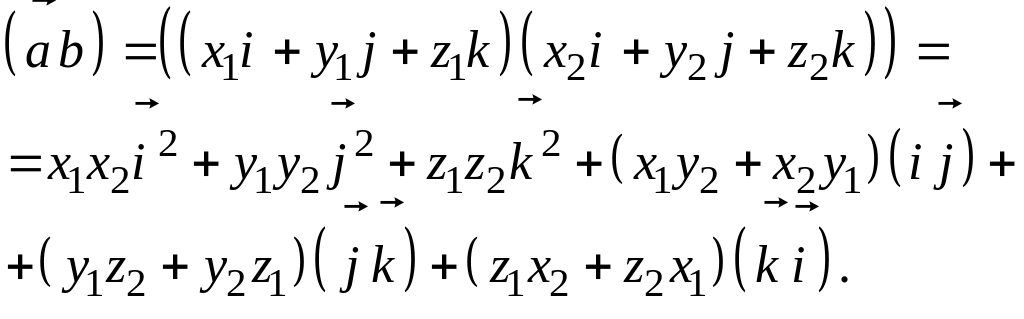
Но так как - единичные попарно ортогональные векторы, то

; ,

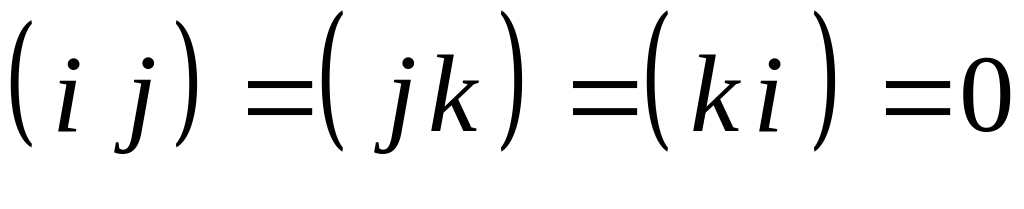значит .

То есть скалярное произведение двух векторов, заданных своими координатами в ортонормированном базисе, равно сумме произведений их соответствующих координат.

В частности

,

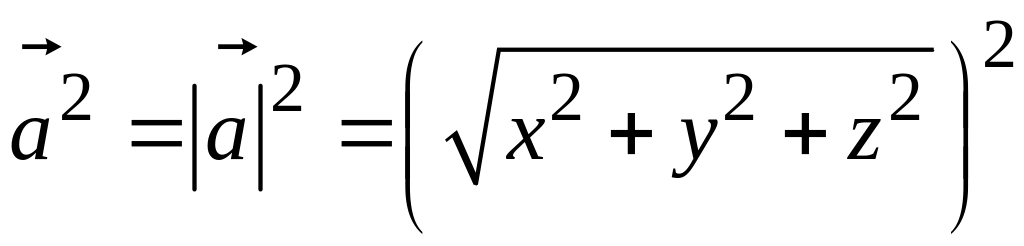где , т.е. модуль вектора равен корню квадратному из суммы квадратов его координат, взятых относительно ортонормированного базиса.

Теперь из формулы находим косинус угла между двумя ненулевыми векторами, заданными своими координатами

;

относительно ортонормированного базиса; именно

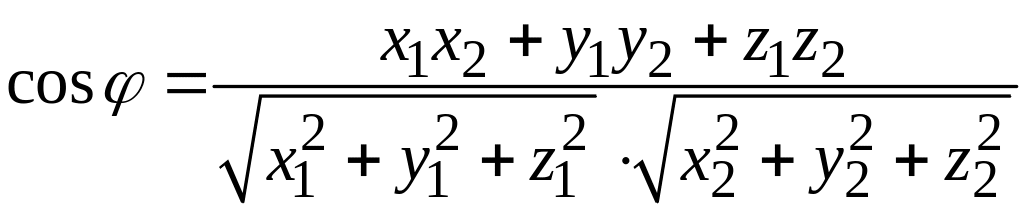. (3)

Из этой формулы находим необходимое и достаточное условие перпендикулярности двух ненулевых векторов:

. (4)

т.е. необходимым и достаточным условием ортогональности двух ненулевых векторов является равенство нулю суммы произведений соответствующих координат, взятых относительно ортонормированного базиса.

Теорема. Координаты x, y, z вектора относительно ортонормированного базиса равны скалярным произведениям этого вектора на единичные векторы базиса, т.е. .

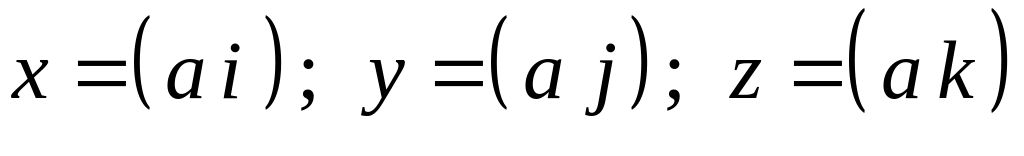Доказательство: на основании теоремы 4 § 37 имеем

.

(теорема 4: коэффициенты в разложении вектора по масштабным векторам , , общей декартовой системы координат в пространстве являются координатами вектора ).

Продолжим доказательство теоремы.

Умножая скалярно обе части этого равенства поочередно на в силу свойств скалярного произведения и соотношений

;

получим:

В частности, если вектор единичный, то

,

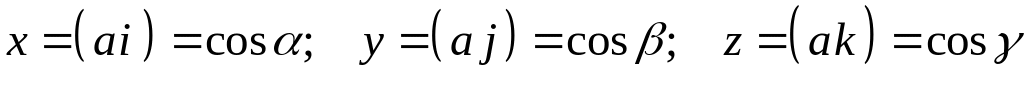где - углы между вектором и векторами .

Так как вектор единичный, то

,

а в силу формулы имеем

.

Таким образом .

Косинусы углов вектора с векторами ортонормированного базиса называются направляющими косинусами вектора или направляющими косинусами оси, имеющей направление вектора .

Мы видим, что сумма квадратов направляющих косинусов оси равна 1.

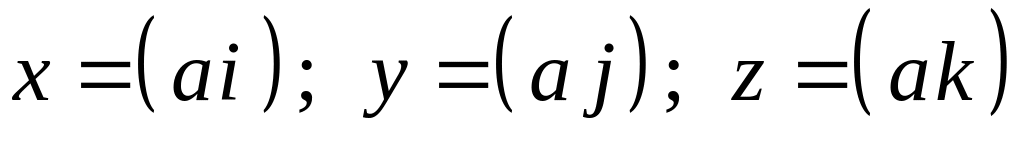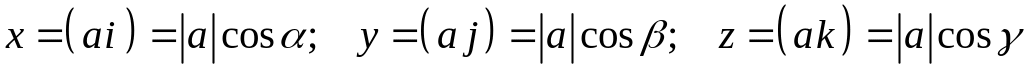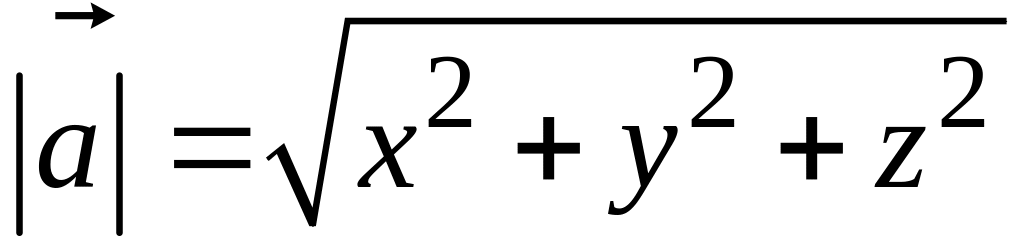Если вектор не единичный, то из соотношений находим и, так как , то

Задачи по Клетенику №№ 795-820.