
- •Введение.
- •Информация и данные.
- •Выч. Система
- •Админ-р
- •Жизненный цикл БнД.
- •Классификация БнД.
- •Преимущества организации субд.
- •Недостатки организации бд.
- •Проектирование бд. (общий подход)
- •Независимость данных (2 уровня).
- •Концептуальное проектирование. Модели данных. Модель сущность-связь.
- •Инфологические мд.
- •Модель результ.
- •Объединение локальных моделей в глобальные.
- •Логическое проектирование.
- •Сетевая модель данных.
- •Правила построения сетевой модели.
- •Реляционная модель данных.
- •Плоский файл.
- •Хронологическая модель данных.
- •Операции над данными.
- •Операции реляционной алгебры.
- •Операторы обновления:
- •Реляционные сравнения:
- •Реляционное исчисление с переменными-кортежами.
- •Реляционное исчисление с переменными на доменах.
- •Реляционные ямд.
- •Язык запросов в sql.
- •Защита баз данных.
- •Функциональные зависимости.
- •Покрытие множества зависимостей.
- •Вычисление замыканий.
- •Декомпозиция схем отношений.
- •Нормализация отношений.
- •Алгоритм1: пополняющий декомпозицию схем отношений, которая обладает свойством соединения без потерь и приводит к отношениям находящимся в нфбк.
- •Алгоритм 2: приведения отношения к 3нф, использующей декомпозицию, сохраняющую функциональные зависимости.
- •Многозначные зависимости.
- •Правила вывода (аксиомы) для многозначных зависимостей.
- •Аксиомы, связывающие функциональные зависимости и многозначные зависимости.
- •Правила вывода:
- •Алгоритм вычисления базиса:
- •Секретность данных.
- •Физическая организация бд.
- •Методы доступа к данным.
- •Оптимизация запросов.
- •Общие стратегии оптимизации:
- •Законы оптимизации.
- •Алгоритм оптимизации выражений ра.
- •Точная оптимизация для подмножества реляционных запросов.
- •Минимизация конъюнктивных запросов.
- •Правила построения табло запросов:
- •Метод нахождения min-го запроса для простого тз.
- •Параллельные операции над бд.
- •Основные понятия.
- •Бесконечные ожидания и тупики.
- •Протоколы и расписание.
- •Простая модель транзакции.
- •Метод, позволяющий определить сериализуемость расписания.
- •Модель с блокировками для чтения и записи.
- •Параллельный доступ к иерархически структурированным элементам.
- •Алгоритм проверки сериализуемости расписания.
- •Защита от отказов.
- •Меры для восстановления бд.
- •Модификация запросов в распределенных бд.
- •Фрагменты отношений.
Законы оптимизации.
З-н коммутативности для соединения и декартова произведения. Если и
 реляционные выражения, а
реляционные выражения, а
 условие, налагаемое на атрибуты
и
,
то:
условие, налагаемое на атрибуты
и
,
то:
![]()
З-н ассоциативности для соединения и декартова произведения:
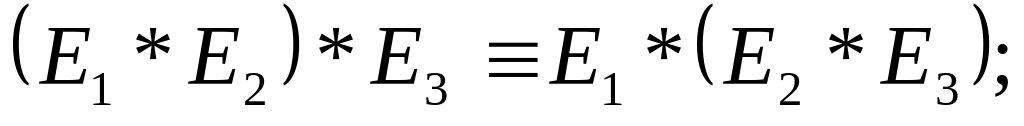
Законы, касающиеся операций селекции и проекции:
Каскад проекций:
 если
если

Следствие: если
проекция по всем атрибутам отношения,
то она растворяется:
![]()
Каскад селекций:

Перестановка селекции и проекции:
 .
.
Следствие: Если
![]() входят в F, то
входят в F, то
![]()
Перестановка селекции с декартовым произведением. Если все атрибуты, упоминающиеся в являются атрибутами , то
 Если в F входят только атрибуты
выражения
Если в F входят только атрибуты
выражения
 то наоборот:
то наоборот:

Следствия:
1. если
имеет вид
![]() ,
где
,
где
![]() включает только атрибуты
,
а
включает только атрибуты
,
а
![]() только атрибуты
,
то в соответствии с законами 1, 4, 6 имеем:
только атрибуты
,
то в соответствии с законами 1, 4, 6 имеем:
![]()
если в используется только атрибут , а в – атрибуты
 ,
то
,
то

Таким образом, часть селекции может быть выполнена до произведения. Соединение всегда может быть выражено как декартово произведение с последующей селекцией, а в случае естественного соединения – проекцией.
Если имена атрибутов в и различаются, мы должны заменить атрибут в правой части формулы соответствующими именами в .
Перестановка селекции с объединением:

Перестановка селекции с разностью:

Перестановка проекции с декартовым произведением.
Пусть
и
– реляционные выражения;
![]() список их атрибутов, причем
список их атрибутов, причем
![]() атрибуты выражения
,
а остальные
атрибуты выражения
,
а остальные
![]() атрибуты выражения
,
тогда:
атрибуты выражения
,
тогда:
![]() .
.
Перестановка проекции с объединением:

Если
имена атрибутов в
и (или)
отличны от имен атрибутов в
,
мы должны заменить
![]() в правой части соответствующими именами.
в правой части соответствующими именами.
Алгоритм оптимизации выражений ра.
Исходные данные – дерево разбора, представляющее выражения РА. Выходные – тоже дерево, но оптимизированное (программа, для вычисления выражения).
Метод:
Каждую селекцию представляем в виде каскада по правилу 4):
 ;
;Перемещаем каждую селекцию насколько это возможно вниз по дереву, используя правила 5)-8);
Перемещаем каждую проекцию в дереве вниз настолько, насколько это возможно, используя правило 3), которое приводит к исчезновению некоторых проекций, следствие из 5), которое расщепляет на несколько, и правила 9) и 10);
Комбинируем каждый каскад селекций и проекций в одиночную селекцию, одиночную проекцию, или селекцию с последующей проекцией, используя правила 3) – 5);
Разбиваем внутренние узлы полученного в результате дерева на группы следующим образом. Каждый внутренний узел представляет собой двуместный оператор (\,
 ),
принадлежащий группе вместе с его
непосредственными предками, которые
помечены унарными операторами (
),
принадлежащий группе вместе с его
непосредственными предками, которые
помечены унарными операторами ( ).
Включаем также в группу любую цепь
потомков данного узла, помеченных
унарными операторами, завершающуюся
в листе.
).
Включаем также в группу любую цепь
потомков данного узла, помеченных
унарными операторами, завершающуюся
в листе.
Исключением является случай, когда двуместный оператор представляет собой декартово произведение без последующей селекции, которая комбинировалась бы с произведением, образуя эквисоединение.
Создаем программу из нескольких шагов для вычисления каждой группы в любом порядке, но так, чтобы никакая группа не вычислялась раньше групп – ее потомков.
Шаги алгоритмов могут быть:
выполнение одиночной селекции или проекции;
выполнение декартового произведения, объединения, либо разности множеств, которые, возможно, предшествуют или за которыми следуют селекция или проекция, применяемая к одному или обоим операндам.
Пример:
Рассмотрим БД «библиотека», состоящую из отношений:
![]() Книги (название; автор; издательство;
инв. №)
Книги (название; автор; издательство;
инв. №)
![]() Издатель (издательство; город; адрес)
Издатель (издательство; город; адрес)
![]() Читатели (ФИО; город; адрес; № читательского
билета)
Читатели (ФИО; город; адрес; № читательского
билета)
![]() Выдача (инв. №; № читательского билета;
дата)
Выдача (инв. №; № читательского билета;
дата)
Для того, чтобы знать,
у кого находится какая книга, можно
использовать отношения
![]() ,
которые могут быть представлены следующим
образом:
,
которые могут быть представлены следующим
образом:
![]() (1)
(1)
F=(R3.№_читательского_билета=R4.№_читательского_билета) (R1.инвентарный_№=R4.инвентарный_№)=F1F2
X= название; автор; издательство; инв. №; ФИО читателя; город; адрес; № читательского билета; дата.
Опишем запрос: перечислить книги, которые были выданы до 01.01.2000.
После подстановки S в (1) получаем следующее дерево разбора:

1-й шаг: расщепление
селекции
![]() на две:
на две:
![]() .
.
2-й шаг: перемещаем
каждую из 3-х селекций как можно ниже в
дереве. Селекцию
![]() перемещаем ниже проекции и двух селекций
по правилам 4) и 5).
перемещаем ниже проекции и двух селекций
по правилам 4) и 5).
Селекция
![]() применяется к
применяется к
![]() ,
и т.к. дата – единственный атрибут
,
и т.к. дата – единственный атрибут
![]() ,
то можно записать:
,
то можно записать:
![]()
Селекция
![]() не может быть перемещена ниже соединения,
т.к. в
используется отношение
и
.
Селекция
не может быть перемещена ниже соединения,
т.к. в
используется отношение
и
.
Селекция
![]() может быть применима к
может быть применима к
![]() .
.
3-й шаг: можно скомбинировать две проекции в одну по правилу 3):

4-й шаг: по обобщенному правилу 5) делаем замену:
![]()
5-й шаг: применим
правило 9) с целью замены последней
проекции на
![]() ,
применим к
и
,
применим к
и
![]() ,
применим к левому операнду декартова
произведения более высокого уровня
(см. последний рисунок).
,
применим к левому операнду декартова
произведения более высокого уровня
(см. последний рисунок).
Последняя проекция взаимодействует с помещенной ниже селекцией по обобщенному правилу 5). В результате получаем каскад:

6-й шаг: последнюю проекцию можно записать в виде (она просеивается через декартово произведение по правилу 9) и частично через селекцию по правилу 5)):
![]()
Так как в проекции упоминаются все атрибуты , то ее удаляем. Каждое из декартовых произведений является фактически эквисоединением, если скомбинировать его с селекцией, находящейся выше в дереве.
Программа, выполняющая этот алгоритм, сначала будет выполнять нижнюю группу, затем верхнюю.
- - - – группы операторов.

|

|

