Функциональные зависимости.

Функциональные зависимости описывают ограничения, которые связаны не с конкретными значениями атрибута, а с тем, совпадают ли определенные компоненты кортежей.

Пусть – схема отношения, а – подмножества (множество атрибутов). Говорят, что X функционально определяет Y (Y функционально зависит от X), и обозначается , если в любом отношении R не существует 2-х кортежей, компоненты которых совпадают по всем атрибутам, принадлежащим , но не совпадают по одному или более атрибутам, принадлежащим Y.

Функциональные зависимости возникают различными способами:

1. Если, например, является ключом, то .

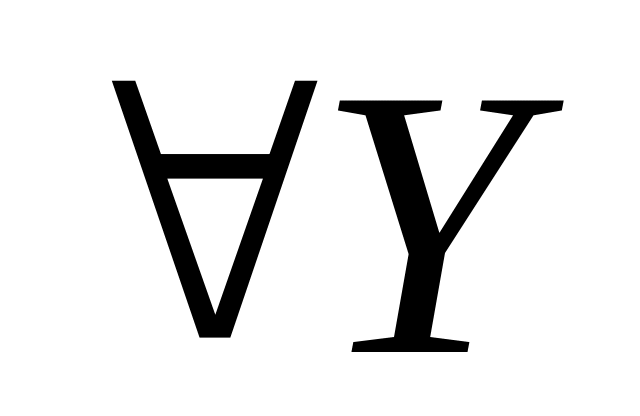2. – есть отображение набора объектов к набору . Среди есть атрибуты, образующие ключ для , и ключ для , то справедливо .

3. и для .

Если заданы функциональные зависимости, то СУБД будет:

а) поддерживать ограничения целостности;

б) более эффективно будет реализовываться отношение, однако при этом будет невозможно хранение некоторой информации. Например, Имя Телефон; то не может быть 2-х телефонов для одного человека.

В связи с введением функциональной зависимости можно дать другое определение ключа:

Если – схема отношения с атрибутами и множество функциональных зависимостей , а подмножество , то X называется ключом отношения R, если

1. , где – замыкание множества функциональных зависимостей;

2. Ни для какого собственного подмножества . F⁺ – все функциональные зависимости, которые могут быть получены для данного отношения с использованием правил вывода.

Правила вывода называются аксиомами функциональной зависимости; пусть задана схема отношения с полным множеством атрибутов и множеством функциональных зависимостей , связывающем только атрибуты из .

1˚. аксиома рефлексивности: Это правило дает тривиальные зависимости, т.е. зависимости, правая часть которых содержится в левой части. Его использование не зависит от .

2˚. аксиома пополнения:

3˚. аксиома транзитивности:

Пример: R(индекс, город, адрес)

F : индекс → город

город, адрес → индекс

F ⁺: индекс, адрес → город, адрес

город, адрес → индекс, город, адрес

индекс, адрес → индекс, город, адрес

Рассмотренные аксиомы являются надежными, т.е. приводят к истинным заключениям. Другие правила вывода, которые являются следствием из 1˚-3˚:

4˚. правило объединения:

5˚. правило декомпозиции: (вытекает из 1˚, 3˚).

6˚. правило псевдотранзитивности:

Правило объединения и декомпозиции порождают важное следствие:

Если – атрибуты, то зависимость справедлива т. и т.т., когда .

Не существует алгоритма для нахождения множества функциональной зависимости.

Покрытие множества зависимостей.

Пусть и – множества функциональных зависимостей. Будем считать, что и эквивалентны, если . В этом случае говорят, что покрывает и, наоборот, покрывает .

Лемма: Каждое множество функциональных зависимостей F покрывается некоторым множеством функциональных зависимостей , в которых ни одна из правых частей не состоит более чем из одного атрибута.

Теорема: Каждое множество функциональных зависимостей F эквивалентно некоторому минимальному множеству .

Говорят, что множество функциональных зависимостей F минимально, если:

1. правая часть каждой зависимости в F состоит только из одного атрибута;

2. ни для какой зависимости в F множество 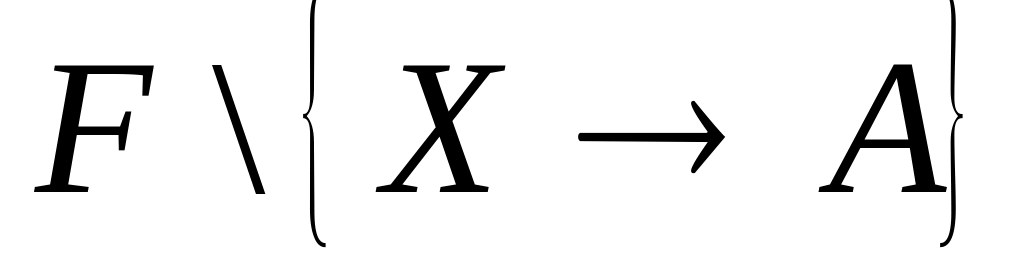не эквивалентно F;

3. ни для какой функциональной зависимости в F и собственного подмножества , множества 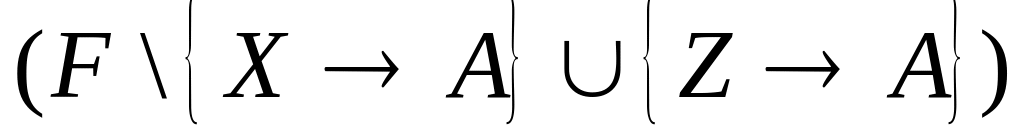и F не эквивалентны.

В общем случае для множества функциональных зависимостей можем построить минимальное.

Замыкание множества атрибутов относительно множества функциональных зависимостей. Пусть F – множество функциональных зависимостей на множестве , и пусть , тогда (замыкание X относительно F) есть множество атрибутов А таких, что зависимость может быть выведена из F по аксиомам 1˚-3˚.

Лемма1: Функциональная зависимость следует из аксиом вывода, если