Задание 401-410.
Вычислить площади фигур, ограниченных линиями
а)
и
.
Решение. I способ
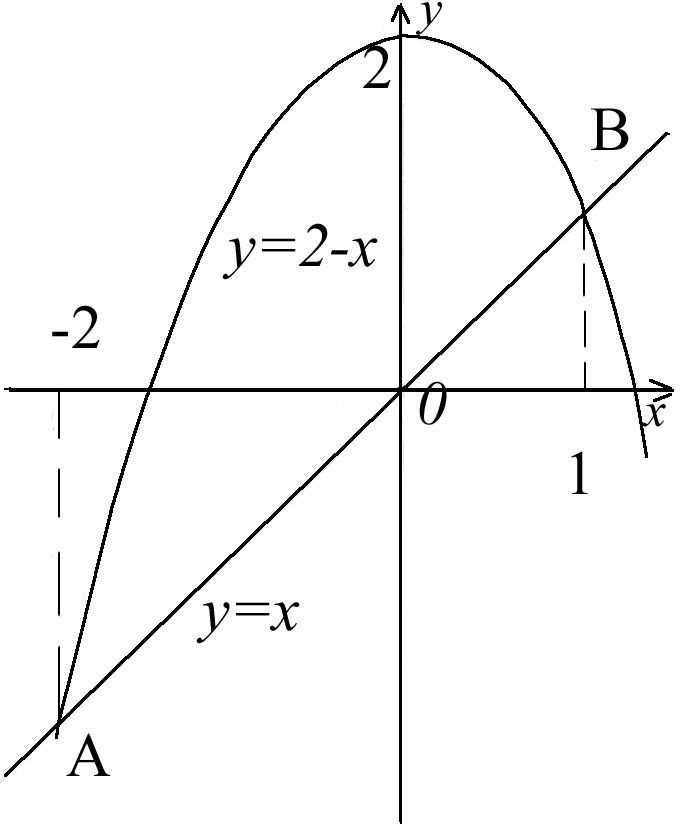
Рис.6
Найдем абсциссы точек A и B, решая совместно уравнения
по формуле (11):
II способ:
по формуле (14):
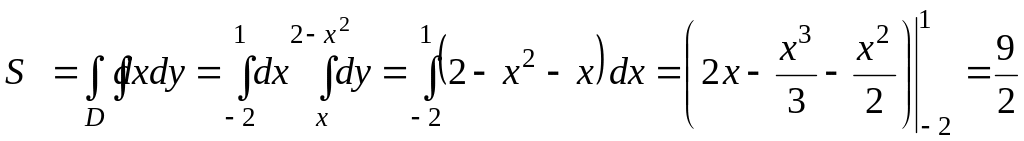
б) найти площадь
одного лепестка кривой
(Рис.7).
Рис.7
Решение.
I способ.
Заметим, что если полярный угол φ изменяется от 0 до π, то точка на кривой обходит против часовой стрелки один лепесток; поэтому по формуле (12) для искомой площади имеем:
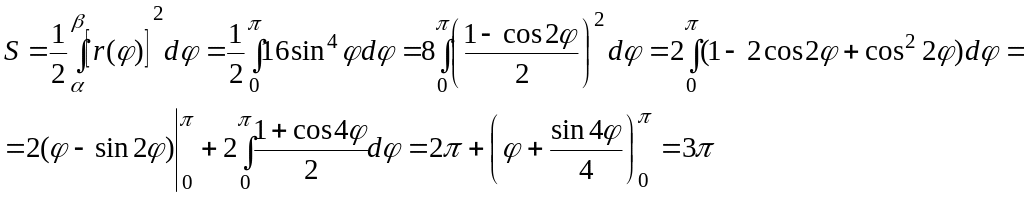II
способ.
по формуле (17) имеем:
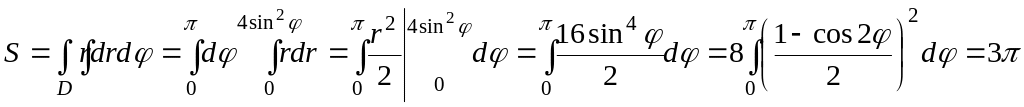
Задание 411-420.
Изменить порядок
интегрирования в повторном интеграле
,
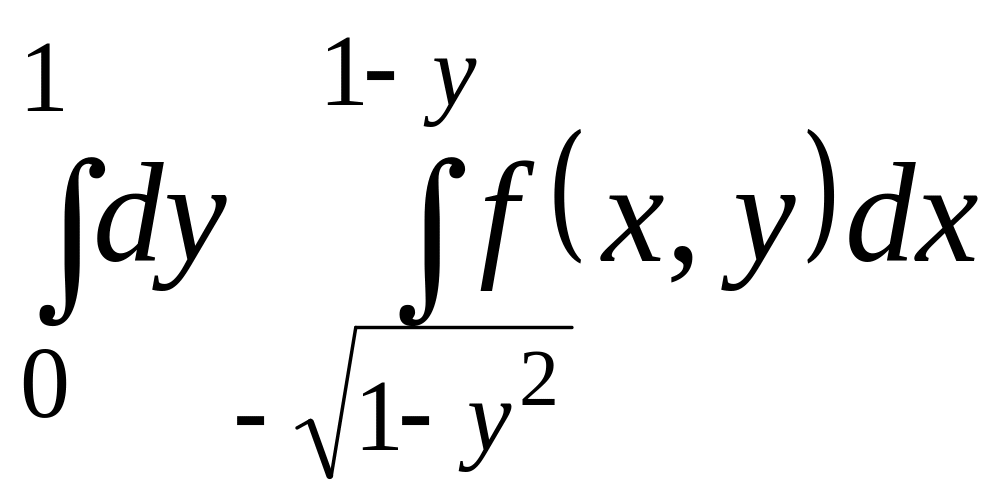предварительно изобразив на чертеже области интегрирования.
Решение. Строим область D по пределам интегрирования
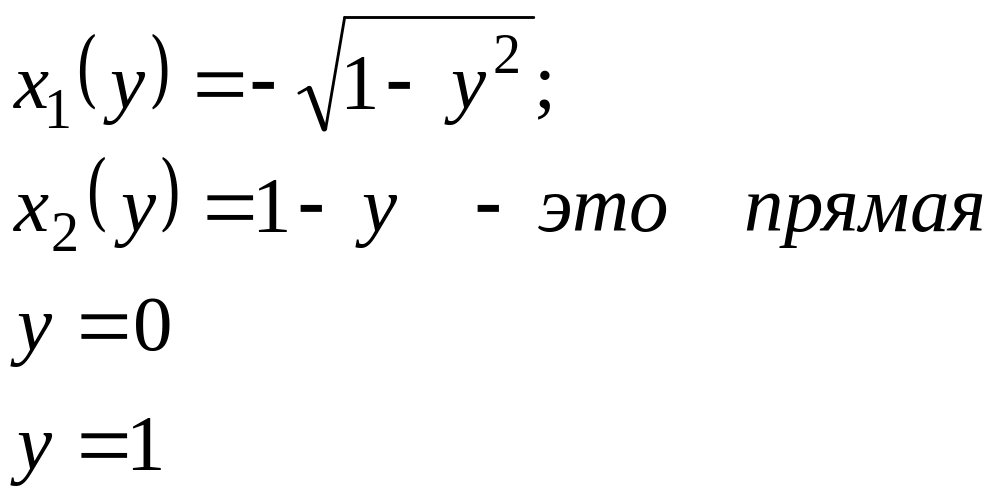
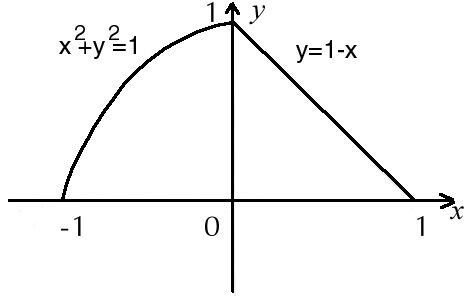
Рис.8
Область такова,
что при вычислении внешнего интеграла
по переменной
верхняя граница области D
описывается двумя уравнениями
,
следовательно, будем иметь
.
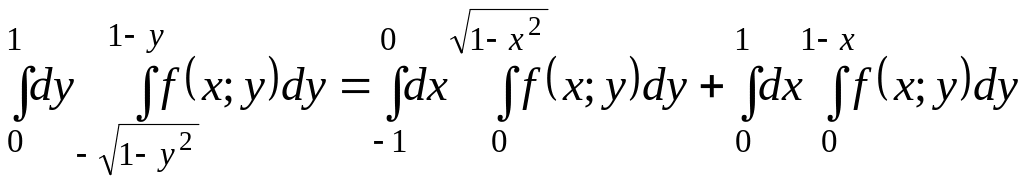Задание 441-450.
Найти работу,
производимую силой
,
вдоль параболы
от точки А(0,0) до точки В(1,1).
Решение.
Из формулы (26) следует, что
.
Так как интегрируем по параболе
и при перемещении из точки А в точку В
меняется от 0 до 1(Рис.9), получаем по
формуле (23), учитывая, что
:
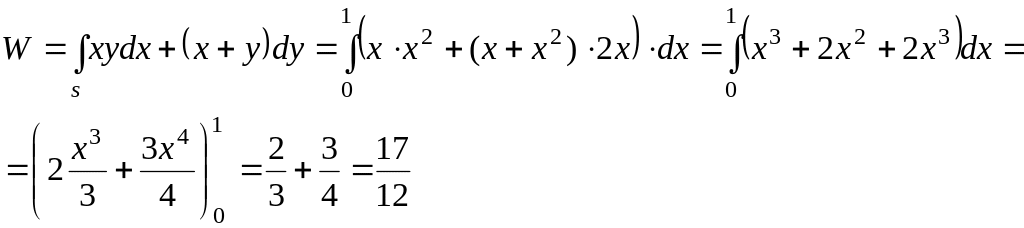
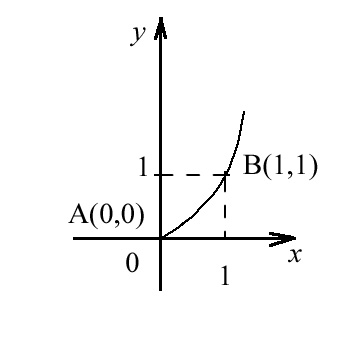
Рис.9
III. Задания к контрольной работе.
1. Задание 361-370.
Дано комплексное число a.
Требуется:
а) записать данное число в алгебраической, тригонометрической и показательной формах;
б) изобразить a на комплексной плоскости;
в) вычислить
г) найти все корни уравнения ;
д) вычислить произведение полученных корней;
е) составить квадратное уравнение с действительными коэффициентами, корнем которого является a.
361.
;
362.
;
363.
;
364.
;
365.
366.
;
367.
;
368.
;
369.
;
370.
Задание 401-410.
Вычислить площади фигур, ограниченных линиями:
401. а)
б)
402.
а)
б)
403.
а)
б)
404.
а)
б)
405.
а)
б)
406.
а)
б)
407.
а)
б)
408.
а)
б)
409.
а)
б)
410.
а)
б)
.
Задание 411-420.
Изменить порядок интегрирования в следующих повторных интегралах,
предварительно изобразив на чертеже области интегрирования.
411.
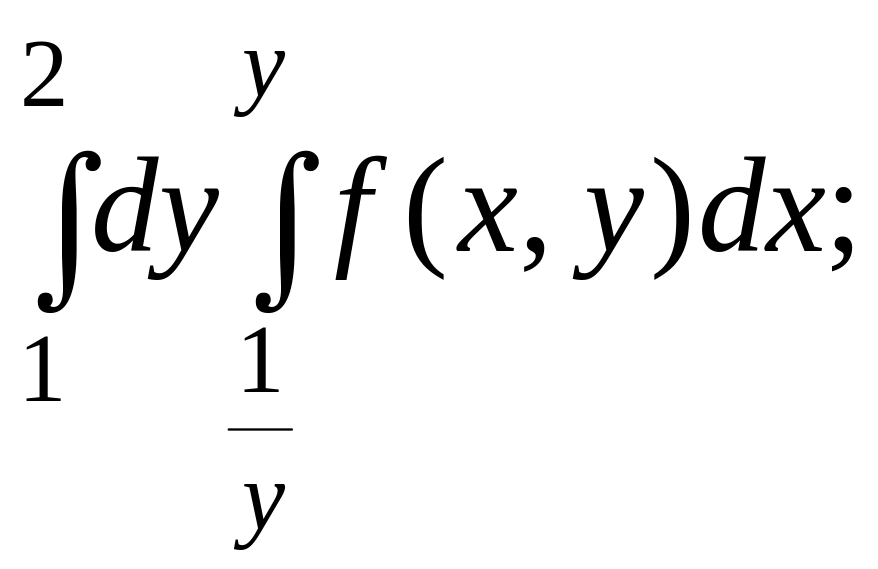412.
413.
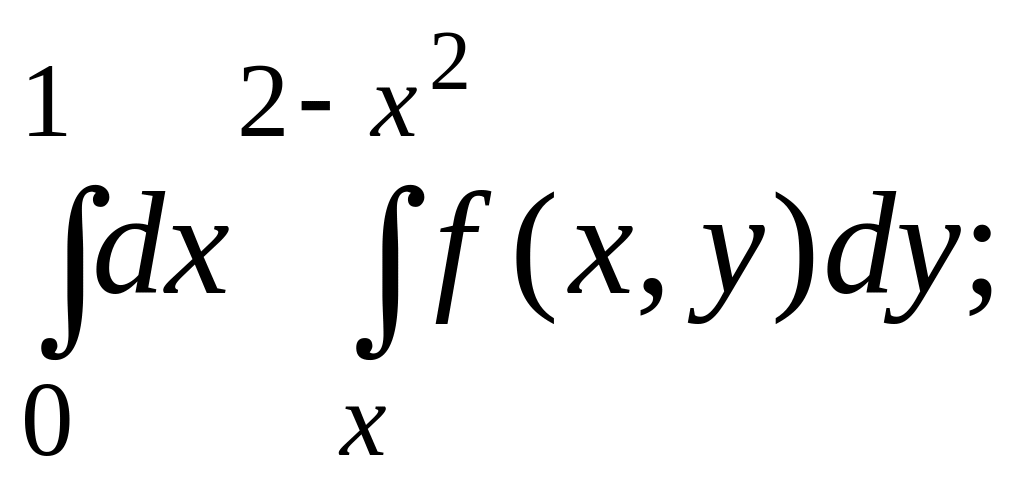414.
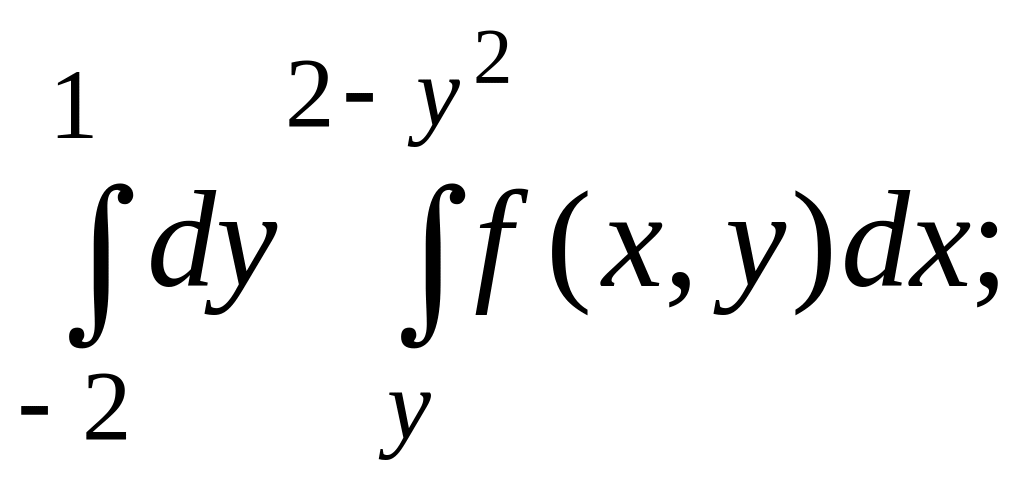
415.
416.
417.
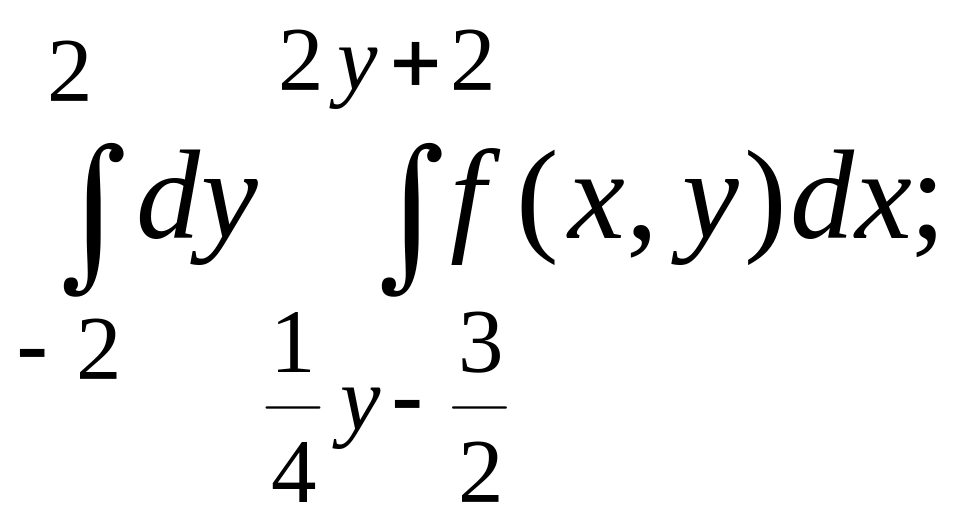418.
419.
420.
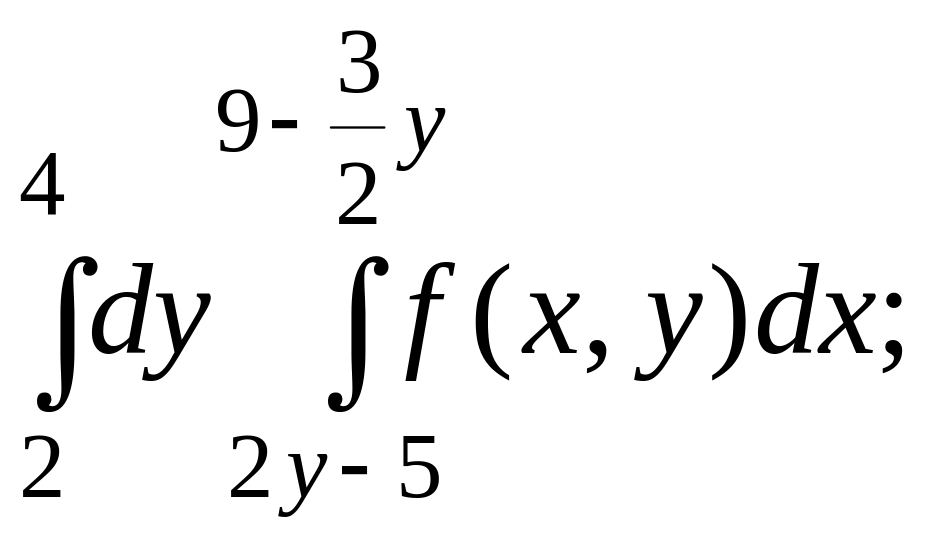
4. Задание 441-450.
Найти работу,
производимую силой
,
вдоль указанного пути L.
Сделать чертеж кривой L.
441.
L – ломаная ОАВ; где (·) О(0;0); (·) А(2;0); (·) В(4;5).
442.
L
– дуга окружности, задаваемой уравнением
;
от (·)А(5;0) до (·) В(0;5).
443.
L
– дуга кривой
.
444.
L – дуга параболы от (·) А(-1,1) до (·) В(1,1).
445.
L – верхняя половина эллипса, задаваемого уравнением
.
446.
L
– дуга кривой
от (·) А(0,1) до (·) В(-1,e).
447.
L – ломаная АВС; где (·) А(1;2); (·) В(1;5) (·) С(3;5).
448.
L
– дуга астроиды
;
449.
L
– дуга параболы
от (·)О(0;0) до (·) А(1;2).
450.
L
– дуга кривой
от (·)А(1;0) до (·) А(e;1).
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
1. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. т.I.,М: Наука, 1985.
2.Ефимов А.В., Демидович Б.П. Сборник задач по математике для втузов,ч.1, М: Наука, 1993.
3.Данко П.Е. и др.Высшая математика в упражнениях и задачах. М: Высшая школа, 1999.
Учебное издание
Лапшина Наталья Валерьяновна, Соловьёва Ирина Михайловна,
Спиридонов Евгений Игоревич, Шварц Михаил Александрович
Кратные и криволинейные интегралы. Контрольная работа № 6
Учебно-методическое пособие
Компьютерная верстка
Редакция авторская
План 2005г. №
__________________________________________________________________
Формат 60х84 1/16 Бумага для множ. апп.
Печать офсетная
Усл.печ.л. 0,8 Усл.изд.л. 0,8 Тираж
Петербургский государственный университет путей сообщения.
190031, Санкт-Петербург, Московский пр., д.9.