4.2. Криволинейный интеграл по координатам (Второго рода)

Криволинейный интеграл от непрерывной в некоторой области плоскости функции по координате вдоль дуги плоской кусочно-гладкой кривой , расположенной в этой области, связан с рассмотренным в пункте 4.1. криволинейным интегралом по длине дуги соотношением

где - угол между касательной, проведенной к кривой в любой ее точке, и положительным направлением оси . Аналогично,

,

где - угол между касательной, проведенной к кривой в любой ее точке, и положительным направлением оси . Очевидно, что и .

Обычно рассматривают сумму интегралов по координате и по координате , которая записывается в виде

(22)

Криволинейные интегралы по координатам обладают теми же простейшими свойствами, что и интегралы по длине дуги. Однако в отличие от последних они зависят от выбора направления обхода кривой: если изменить направление обхода кривой, то интеграл (22) меняет знак, то есть

Для вычисления интеграла (22) пользуются одной из следующих формул:

a). если кривая задана уравнением и при перемещении из точки А в точку В меняется от до , то

; (23)

b). если кривая задана уравнениями и при перемещении из точки А в точку В параметр меняется от до , то

. (24)

Замечание. В случае замкнутой кривой условимся брать направление обхода кривой так, чтобы область, ограниченная этой кривой, всегда оставалась слева.

Аналогично определяются криволинейные интегралы по координатам в случае, если кривая лежит в плоскости или и от непрерывных в некоторой пространственной области функций вдоль дуги пространственной кусочно-гладкой кривой , расположенной в этой области, то есть

.

Если кривая задана параметрическим уравнением

,

то

(25)

3. Приложения криволинейных интегралов (вычисление работы силы).

Пусть есть переменная сила, совершающая работу вдоль пути , и функции и непрерывны на кривой ; тогда

. (26)

II. Пример выполнения контрольной работы.

1. Задание 361-370.

Дано комплексное число .

Требуется:

а) записать данное число в алгебраической, тригонометрической и показательной формах;

б) изобразить a на комплексной плоскости;

в) вычислить

г) найти все корни уравнения ;

д) вычислить произведение полученных корней;

е) составить квадратное уравнение с действительными коэффициентами, корнем которого является a.

Решение.

а) Используем формулу (3)

Получили чисто мнимое число a=0+i в алгебраической форме.

Вычислим модуль и аргумент полученного числа. По формулам (4) и (5):

- не существует, но ( ), следовательно .

По формуле (6) запишем тригонометрическую форму числа a:

и по формуле (9) в показательной форме:

б) Изобразим число a=0+i на комплексной плоскости (Рис.5).

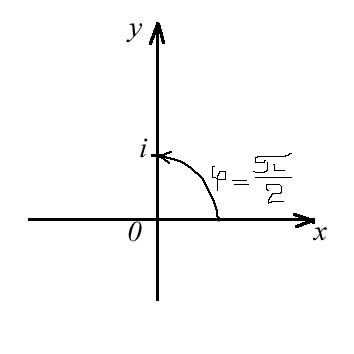
Рис.5

в) вычислим по формуле (7):

г) найдем все корни уравнения :

. Найдем все корни используя формулу (8):

д) вычислим произведение полученных корней:

е) составим квадратное уравнение с действительными коэффициентами, корнем которого является a:

Раз a- корень квадратного уравнения, значит и сопряженное ему комплексное число тоже будет корнем этого уравнения и, следовательно, уравнение имеет вид:

, т.е.