3.2. Перемена порядка интегрирования.

Если область D является простой как вида 1, так и вида 2, то применимы обе формулы (12) и (13), следовательно,

Иными словами, повторное интегрирование не зависит от порядка интегрирования. Этим обстоятельством часто пользуются при вычислении двойного интеграла, выбирая ту из двух формул (12) и (13), которая приводит к более простым выкладкам.

Задача об изменении порядка интегрирования в повторном интеграле применяется в качестве упражнения на расстановку пределов

Прежде всего, следует начертить область интегрирования D, которая находится в полосе между прямыми и ограничена снизу линией , а сверху – линией . Затем область D проектируют на ось и находят уравнения прямых , ограничивающих снизу и сверху полосу, в которой расположена область D, затем находят левую границу области D

и правую . Если какая-либо из этих границ состоит из двух или большего числа линий, записанных разными уравнениями, то область D приходится разбивать на части, а интеграл – на сумму интегралов по этим частям.

Аналогично, если требуется изменить порядок интегрирования в повторном интеграле

,

то, спроектировав область D на ось , находят уравнения прямых , нижнюю границу области D и верхнюю . Иногда область D приходится разбивать на части, а интеграл – на сумму интегралов по этим частям.

3.3. Замена переменной в двойном интеграле

Пусть на плоскости дана ограниченная область D.

Предположим, что координаты и являются функциями новых переменных , причем эти функции однозначны, непрерывны и имеют непрерывные производные в области D₁ в плоскости UO'V и при этом якобиан сохраняет постоянный знак в области D, тогда справедлива формула

(14)

Наиболее употребительными являются полярные координаты ,

для которых якобиан и формула (14) принимает вид:

(15)

Если область ограничена лучами  и кривыми и – однозначные функции на , то двойной интеграл может быть вычислен по формуле

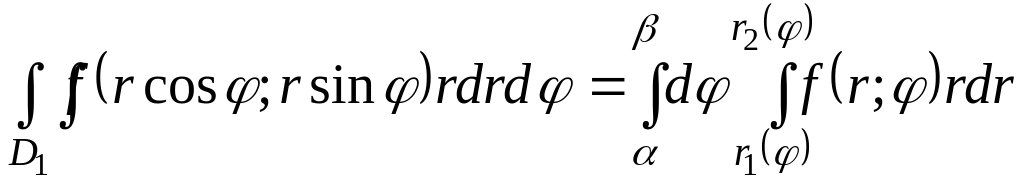
3.4. Вычисление площадей плоских областей.

Площадь S плоской области D на плоскости в прямоугольных координатах вычисляется

по формуле

, (16)

а в полярных координатах по формуле

(17)

4. Криволинейные интегралы

4.1. Криволинейные интегралы по длине дуги (Первого рода)

Пусть есть функция, непрерывная в некоторой области на плоскости , и – некоторая кусочно-гладкая кривая*, расположенная в этой области.

(* Кривая называется гладкой, если в каждой ее точке существует касательная, непрерывно изменяющаяся вдоль кривой. Кусочно-гладкой кривой называется непрерывная кривая, состоящая из конечного числа гладких кусков). Разобьем кривую системой точек на элементарные дуги . На каждой элементарной дуге (i=1, 2, 3,…n) выберем произвольную точку и умножим значение функции в этой точке на длину элементарной дуги . Сумма таких произведений по всем элементарным дугам

называется интегральной суммой. Обозначим наибольшую из длин всех элементарных дуг.

Определение. Криволинейным интегралом от функции по длине дуги кривой называется предел интегральных сумм при неограниченном увеличении числа элементарных дуг, когда все элементарные дуги стягиваются в точку:

Криволинейный интеграл по длине дуги обладает следующими простейшими свойствами:

1.

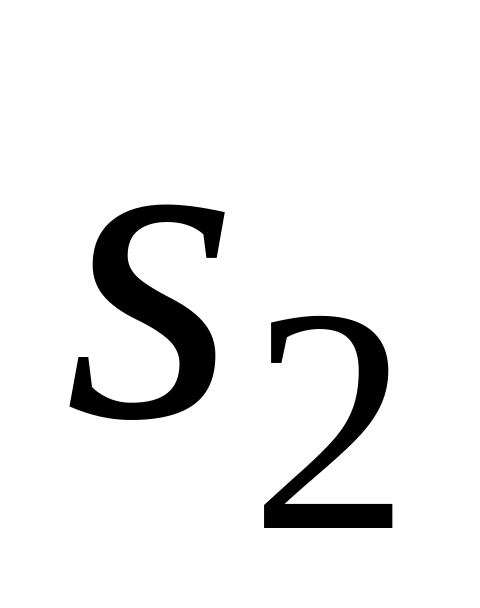2. если кривая s состоит из двух кривых и , то

По своему определению криволинейный интеграл по длине дуги не зависит от направления дуги интегрирования, то есть

Для вычисления криволинейного интеграла по длине дуги пользуются одной из следующих формул:

a). если кривая задана уравнением y =  (x) (a  x  b),

то

и

(18)

b). если кривая задана параметрически:

x =  (t), y =  (t) (  t  ),

то

и

(19)

с). если кривая задана уравнением (   ),

то

и

(20)

Аналогично определяются криволинейные интегралы от непрерывной в некоторой пространственной области функции по длине дуги пространственной кусочно-гладкой кривой S, расположенной в этой области, то есть

Если кривая задана параметрическими уравнениями

, (  t  ),

то

и

(21)