Параметричні рівняння кривої

Інколи зручно рівняння кривих задавати чи виводити їх в декартовій системі координат за допомогою параметрів. Вводять параметр t і через нього виражають x і y -- координати точок кривої.

Параметричні рівняння кривої:

на площині

в просторі. Т – проміжок зміни параметра (Тℝ) .

Приклад 1. Циклоїда — це крива, що описується точкою, що лежить на колі, якщо це коло котиться по прямій, без проковзування. Скласти її рівняння.

Приймемо вісь Ох як пряму, по якій котиться коло радіуса а. В початковий момент часу нехай точка на колі лежить в початку координат. Нехай коло прокотилось так, що його центр в точці О₁, а точка , за якою ми спостерігаємо, перемістилась в точку М. Позначимо через t кут , який утворює радіус О₁М з від’ємним напрямком осі Оу:  MО₁K=t. Дуга МК дорівнює ОК, отже ОК=аt.

Розглянемо трикутник MО₁K: МР=аcost, О₁P=asint. Тоді для координат (х,у) точки М маємо: x=OK-MP=at-acost=a(t-cost),

y =О₁P- О₁K=a-asint=a(1-sint).

M

O₁

t P

О₁

O K

O P

Циклоїда описується параметричними рівняннями: .

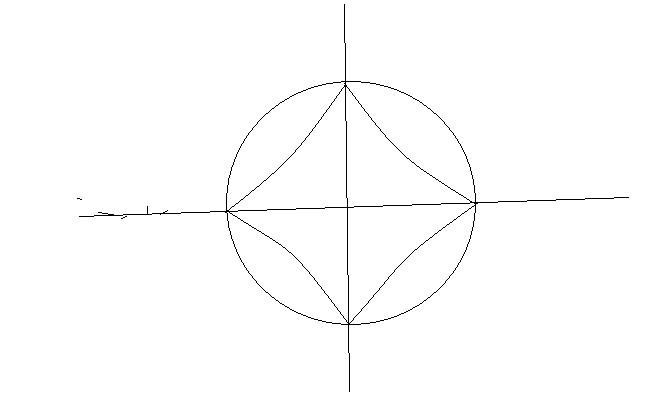
Приклад 2. Астроїда -- крива, що описується точкою, що лежить на колі з радіусом а/4, яке котиться по колу з радіусом a всередині. Скласти її рівняння.

Нехай центр нерухомого кола (з радіусом а) в початку координат. В початковий момент часу «мале» (з радіусом а/4) коло дотикається до нерухомого в точці на осі Ох з координатами (а,0). Ця точка дотику на «малому» колі і буде спостережуваною точкою. Нехай «мале» коло прокотилось так, що його центр – в точці О₁, а спостережувана точка в точці М (див. мал.). Нову точку дотику позначимо К, кут О₁ОО₂ позначимо через t. Оскільки довжина дуги NK дорівнює довжині дуги МК, але радіус малого кола в 4 рази менший, то кут КО₁М=4t. З малюнка КОN=КО₁Р= t, тому МО₁Р = 4t - t = 3t.

Розглянемо прямокутний трикутник МО₁Р: О₁Р=a/4 cos 3t, PM=a/4 sin 3t.

Тоді для координат (х,у) точки М маємо: х=ОО₂+О₁Р=3а/4 соs t + a/4 cos 3t,

Y=OO₃-PM=3a/4 sin t - a/4 sin 3t.

N

O₃

О O₂

О₁

P

M

К

, бо

Аналогічно для у. Щоб пройти всю астроїду один раз достатньо взяти

Отже, – параметричні рівняння астроїди.

Можна виключити параметр t, отримаємо непараметричне рівняння астроїди: