2) Рівняння площини через три точки. Нехай є три точки у просторі М₁(х₁,y₁,z₁), М₂(х₂,y₂,z₂), М₃(х₃,y₃,z₃). Якщо вони не лежать на одній прямій, то існує єдина площина П, що проходить через ці три точки. Скласти її рівняння.

М₂ М

М₁ М₃

М₂

П

Точка М(x,y,z)  П тоді і тільки тоді, коли вектори, які виходять з однієї точки, наприклад з точки М₁, лежать в одній площині, тобто компланарні, - компланарні  В координатній формі отримаємо рівняння:

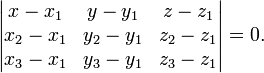
3) Рівняння площини у відрізках. Нехай відомо, що площина відсікає на осях Ox,Oy і Oz відрізки де a = − D / A,b = − D / B,c відповідно. Отже, вона проходить через точки М₁(a,0,0), М₂(0,b,0), М₃(0,0,c). Складемо рівняння площини

Розкривши визначник, отримаємо рівняння:

Зауваження. Якщо задано загальне рівняння площини Ax+By+Cz+D=0, то при D0, перенесемо D в праву частину і поділимо рівняння на -D. Отримаємо таке ж рівняння, де a=−D/A, b=−D/B, c=−D/C — відрізки, які площина відтинає на осях Ox,Oy і Oz відповідно.

Кут між площинами: Дві площини задано загальними рівняннями:

A₁x+B₁y+C₁z+D₁=0; A₂x+B₂y+C₂z+D₂=0;

N₁=(A₁,B₁,C₁),N₂= (A₂,B₂,C₂) - нормальні вектори до них.

Кут між векторамиN₁,N₂ буде одним із кутів між площинами. Для гострого кута : cos = . (Тому, що cos( - α)= - cosα. )

Паралельність, перпендикулярність площин:

П₁ ⃦ П₂  N₁ ⃦N₂  = ;

П₁  П₂  N₁ N₂  A₁A₂+B₁B₂+C₁C₂ = 0;

Аналогічно як відстань від точки до прямої (на площині), можна вивести формулу відстані від точки М₀(х₀,y₀,z₀) до площини П: Ax+By+Cz+D=0.

Пряма в просторі

1. Пряма в просторі l – це перетин двох площин П₁ і П₂:

— загальні рівняння прямої l у просторі.

2. Рівняння прямої через точку М₀(х₀,y₀,z₀) і напрямний (паралельний) вектор  = (m,n,p). (0). Виводиться як на площині:

; ці ж рівняння називають також канонічними рівняннями прямої в просторі.

Позначимо це відношення через t, t – параметр, t(-∞;∞), отримаємо

параметричні рівняння прямої:

, t  ℝ.

3. Рівняння прямої через дві точки.

Точка M(x,y,z) лежить на прямій M₁M₂ (M₁(x₁,y₁,z₁), M₂(x₂,y₂,z₂) ) тоді і тільки тоді, коли вектори колінеарні:

.

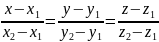Кут між прямими це кут між відповідними напрямними векторами. Для гострого кута: cos α= .

Кут між прямою і площиною. Нехай задані рівняння прямої і площини:

, Ax+By+Cz+D=0. Позначимо через β кут між напрямним вектором прямої = (m,n,p) і нормальним вектором площини N=(A,B,C), а кут між прямою і площиною через α. Тоді .

Ми можемо знайти cos β, а cosβ =cos(

Отже, для гострого кута α маємо:

sin α= . (Тому, що sin(

Розглянемо деякі задачі з рівняннями площини та прямої у просторі.

1. Перехід від загальних рівнянь прямої до канонічних.

 N₂

N₁

Пряма в просторі l – це перетин двох площин П₁ і П₂: Це загальні рівняння прямої.

Для того щоб скласти канонічні рівняння прямої, потрібно знайти напрямний вектор прямої і координати одної точки на прямій.

N₁=(A₁,B₁,C₁),N₂= (A₂,B₂,C₂) - нормальні вектори до площин. Напрямний вектор до прямої є перпендикулярним до векторівN₁,N₂, отже, паралельний до векторного добуткуN₁ N₂.

Для того щоб знайти точку на прямій, можна одній невідомій надати конкретного значення (наприклад, z=0), отримаємо систему рівнянь 22 для знаходження інших координат точки.

Приклад. Перейти від загальних рівнянь прямої до канонічних. .

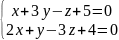N₁=(1,3,-1),N₂=(2,1,-3) – перпендикулярні вектори до напрямного вектора.

 =N₁ N₂= 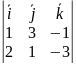=i(-9+1) -j(-3+2) +k(1-6) = (-8;1;-5).

Нехай z=5, то система прийме вигляд:

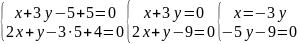
Отже, точка М(5,4; -1,8; 5) лежить на прямій. Тоді

– канонічні рівняння прямої.

2. Перетин прямої та площини

Перетин прямої та площини це точка (або  ). ЇЇ зручно шукати, якщо пряма задана параметричними рівняннями, а площина загальним рівнянням.

Нехай задана пряма l: , t  ℝ і площина П: Ax+By+Cz=0.

Щоб знайти їх перетин потрібно об’єднати всі рівняння і розв’язати систему. Зручно в рівняння площини підставити х,у,z з рівнянь прямої через параметр t.

Отримаємо одне рівняння з одною невідомою t (лінійне). Знайшовши t підставимо його в параметричні рівняння прямої, щоб отримати координати точки перетину.

Приклад. Знайти точку перетину прямої та площини: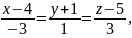

4x-3y+z-3=0.

Перейдемо до параметричних рівнянь прямої: 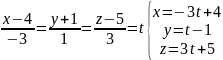. Підставимо в рівняння площини:

4(-3t+4)-3(t-1)+3t+5-3=0  -12t+21=0  t=21/12=7/4=1,75. Підставимо в параметричні рівняння: x= -1,25; y=0,75; z=10,25.

Перевірка: Точка з такими координатами належить прямій, бо вона отримана з параметричних рівнянь при деякому значенні t, тому потрібно підставити точку тільки в рівняння площини: 4(-1,25)-30,75+10,25-3=0  0=0.

Відповідь: М(-1,25; 0,75; 10,25).