В) Обчислення визначників n-го порядку

В пункті а) отримано формулу, яка дає можливість обчислення визначника n-го порядку:

де M_ij – мінор матриці, який відповідає елементові a_ij (j=1,2,…,n). Добуток

(-1)^i+jM_ij називають алгебраїчним доповненням елемента а_ij у визначнику і позначають А_ij .

Теорема 6.1. Визначник матриці А дорівнює сумі добутків усіх елементів будь-якого його рядка на їх алгебраїчні доповнення.

.

Доведення.

При і=1 твердження справедливе:

.

Замінивши тепер кожен добуток на А_1j, отримаємо:

.

Нехай і>2 . Переставляючи послідовно і-й рядок визначника з кожним, що стоїть над ним, через і-1 переставлянь отримаємо визначник:

.

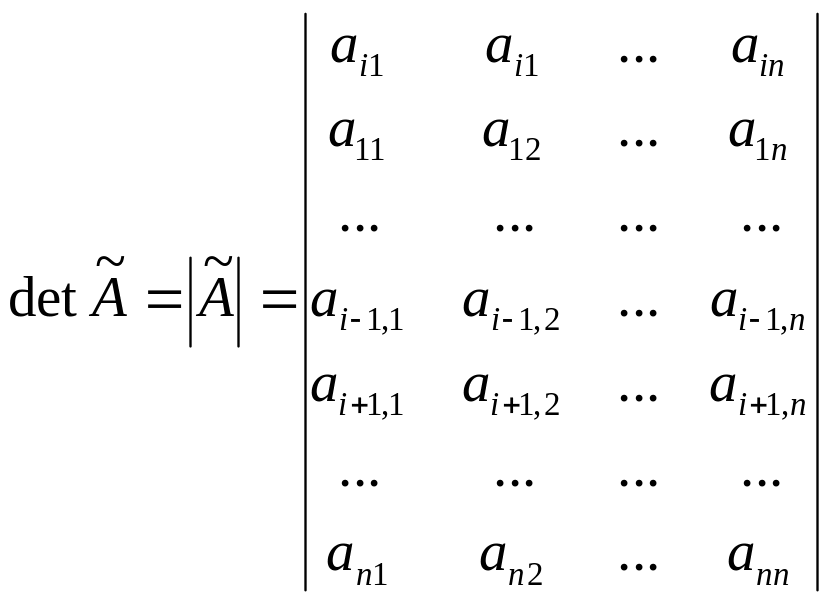(згідно власт. 2), звідки .

Застосуємо до визначника відоме означення, отримаємо

.

Підставимо це значення в det A:

, тобто

Оскільки , то

.

Із того, що , випливає

,

що й треба довести.▲

Оскільки рядки і стовпчики визначника рівноправні, то аналогічний розклад можливий і за елементами довільного стовпчика.

Теорема 6.2. Сума добутків всіх елементів деякого рядка визначника detA на алгебраїчні доповнення відповідних елементів іншого рядка дорівнює нулю:

Доведення.

Розкладемо визначник detA за елементами s-го рядка:

Алгебраїчні доповнення А_sj (j=1,2,...,n) не залежать від елементів а_sj, тому остання рівність буде справедливою при будь-яких значеннях елементів а_sj , зокрема й при а_sj = а_ij (тобто, коли на місці елементів s-го рядка знаходитимуться елементи і-го рядка). Але при а_sj=а_ij визначник detA матиме два однакові рядки і тому дорівнюватиме нулю. Тому

,

що й треба довести. ▲

Ясно, що аналогічний висновок має місце і для розкладу за елементами довільного стовпчика.

Приклад.

Обчислити визначник, розклавши його за елементами 3 рядка:

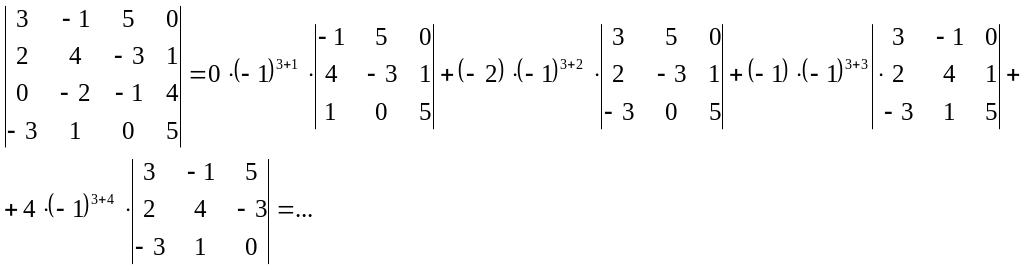
Чим більше елементів у рядку (чи стовпчику) визначника дорівнюють нулю, тим простішим є розклад визначника за елементами даного рядка. Ясно, що найпростішим є варіант, коли деякий рядок (стовпчик) містить тільки один ненульовий елемент. Цього можна добитися з допомогою виконання над рядками (стовпчиками) визначника відповідних елементарних перетворень. Зокрема, в деякому j-тому стовпчику можна отримати нуль в деякому і-му рядку, якщо відняти від і-го рядка, наприклад, перший рядок, помножений на , чи другий рядок, помножений на і т. д.

Приклад.

Обчислити визначник: .

Розв’язування.

Виберемо 4^й стовпчик: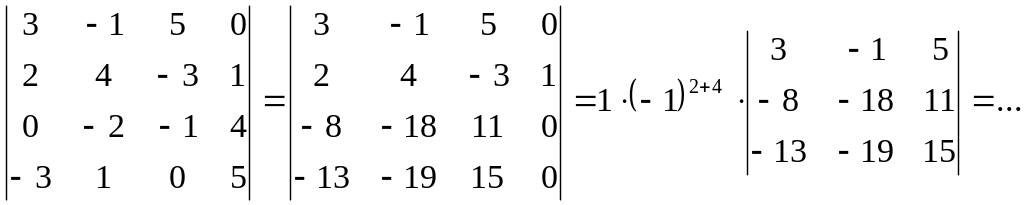

Виберемо 4^й рядок:

11