
Тема 3. Векторные пространства. Системы линейных уравнений Основные определения и понятия темы
Линейно зависимая и линейно независимая системы векторов ([1], стр. 176), базис и ранг системы векторов ([1], стр. 182-183), векторное пространство над полем ([1], стр. 245), подпространство ([1], стр. 250), линейная оболочка системы векторов ([1], стр. 250), базис и размерность конечномерного векторного пространства ([1], стр. 256, 260), координаты вектора в базисе ([1], стр. 265), изоморфизм векторных пространств ([1], стр. 266);
система линейных уравнений с n неизвестными ([1], стр. 185), решение системы линейных уравнений ([1], стр. 185), совместная, несовместная, определенная, неопределенная системы линейных уравнений ([1], стр. 186), равносильные системы линейных уравнений ([1], стр. 186), однородная система линейных уравнений с n неизвестными ([1], стр. 193), фундаментальный набор решений однородной системы линейных уравнений ([1], стр. 204).
Основные теоремы и утверждения темы
Свойства линейно зависимой и линейно независимой систем векторов ([1], стр. 176), простейшие свойства векторных пространств ([1], стр. 247), критерий для подпространства ([1], стр. 250), теорема о размерности суммы подпространств ([1], стр. 261), теорема об изоморфизме векторных пространств одинаковой размерности ([1], стр. 269), теорема о множестве решений однородной системы линейных уравнений ([1], стр. 196), теорема о связи множества решений неоднородной системы уравнений и множества решений соответствующей однородной системы уравнений ([1], стр. 194).
Образцы решения задач
Задание 1. Решить систему линейных уравнений методом последовательного исключения неизвестных (методом Гаусса):
 .
(1)
.
(1)
Решение.
Составим расширенную матрицу системы (1) и приведем ее с помощью элементарных преобразований к ступенчатому виду:









 ∿
∿



 ∿
∿
 ∿
∿



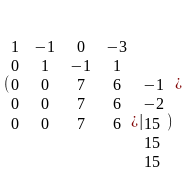 ∿
∿
 .
.
Отсюда
следует, что ранг расширенной матрицы
 системы
(1) равен 3 (число ненулевых строк в матрице
после приведения ее к ступенчатому
виду) и равен рангу основной матрицы
системы (матрицы из коэффициентов при
неизвестных). Поэтому, согласно теореме
Кронекера-Капелли, система (1) является
совместной. Так как ранг расширенной
матрицы не равен числу неизвестных, то
система (1) является неопределенной.
Запишем систему линейных уравнений,
соответствующую ступенчатой матрице:
системы
(1) равен 3 (число ненулевых строк в матрице
после приведения ее к ступенчатому
виду) и равен рангу основной матрицы
системы (матрицы из коэффициентов при
неизвестных). Поэтому, согласно теореме
Кронекера-Капелли, система (1) является
совместной. Так как ранг расширенной
матрицы не равен числу неизвестных, то
система (1) является неопределенной.
Запишем систему линейных уравнений,
соответствующую ступенчатой матрице:
(2)
 .
.
Отметим,
что системы (1) и (2) являются равносильными,
т.е. множества их решений совпадают. В
системе (2) неизвестные
 являются главными, а
являются главными, а
 - свободная неизвестная. Найдем общее
решение системы (2), а значит, и системы
(1):
- свободная неизвестная. Найдем общее
решение системы (2), а значит, и системы
(1):


 ,
,
т.е. общее решение системы (1) имеет вид


 ℝ.
ℝ.
Придавая
произвольные значения, можно получить
частные решения системы (1). Например,
 или
или
 .
.
Задание 2. Установить, является ли данная система векторов линейно зависимой или линейно независимой двумя способами:
а) на основании определения;
б) при помощи матрицы из координат векторов:
 .
.
