6.2. Расчет внецентренно сжатых колонн
В том случае, когда линия действия сжимающей силы не совпадает с осью колонны, в поперечных сечениях колонны кроме продольной силы возникает изгибающий момент (рис. 43).
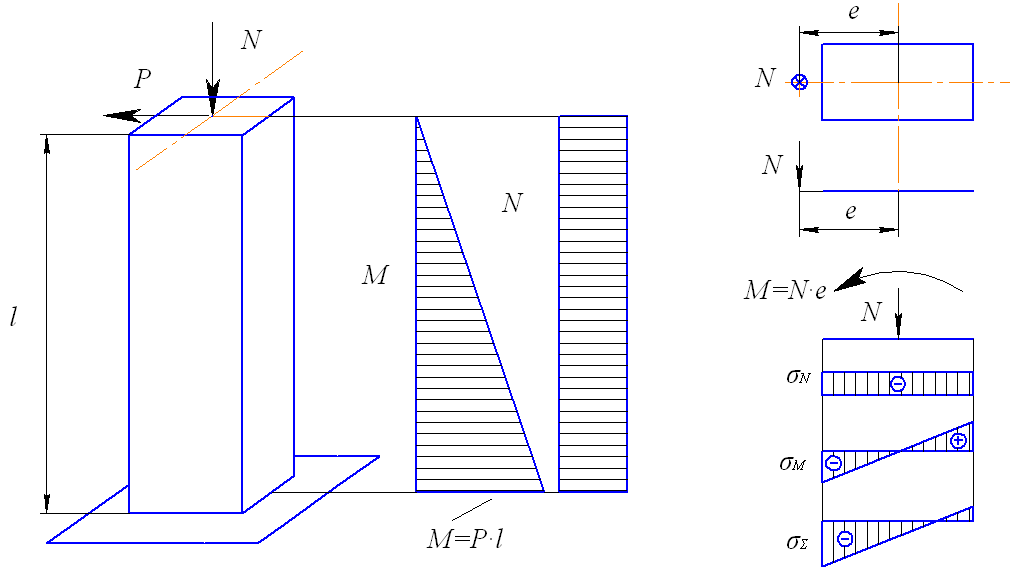
Рис. 43. Внецентренно сжатая колонна.
Тогда в случае изгиба в одной плоскости условие прочности запишется следующим образом
.
(6.17)
А при изгибе в 2-х плоскостях
(6.18)
где
– координаты наиболее опасной точки.
Устойчивость
колонны в плоскости действия изгибающего
момента
проверяют
с учетом коэффициента
,
который зависит от гибкости колонны
(6.19)
где
– продольная сила, приложенная с
эксцентриситетом
;
–
коэффициент
устойчивости, определяемый в зависимости
от условной гибкости
,
(6.20)
где
и приведенного относительного эксцентриситета
,
(6.21)
где
относительный эксцентриситет;
–
коэффициент влияния
формы сечения, который для двутавра
определяется (таб. 6.1) в зависимости от
,
и отношения
где – площадь полки двутавра;
– площадь стенки двутавра.
Таблица 6.1
|
|
||
0≤ ≤5 |
>5 |
||
|
|
|
|
0,25 |
(1,45-0,05)-0,01(5-
) |
1,2 |
1,2 |
0,5 |
(1,75-0,1)-0,02(5- ) |
1,25 |
1,25 |
≥1,0 |
(1,90-0,1)-0,02(6-m) |
1,4-0,02 |
1,3 |
Для других сечений коэффициент определяется по таблице 73 (СНиП II-23-81).
Коэффициенты e для проверки устойчивости внецентренно-сжатых сплошностенчатых стержней в плоскости действия момента, совпадающей с плоскостью симметрии, определяется по таблице 74 (СНиП II-23-81). В таблице 6.2 приведены некоторые значения e.
Таблица 6.2
Условная гибкость
|
Коэффициент e при приведенном относительном эксцентриситете mеf |
||||||||
|
0,1 |
1,0 |
2,0 |
4,0 |
6,0 |
8,0 |
10,0 |
14,0 |
20,0 |
0,5 |
0,967 |
0,722 |
0,538 |
0,337 |
0,237 |
0,210 |
0,150 |
0,106 |
0,077 |
1,0 |
0,925 |
0,653 |
0,484 |
0,307 |
0,225 |
0,196 |
0,142 |
0,103 |
0,074 |
2,0 |
0,813 |
0,536 |
0,397 |
0,260 |
0,193 |
0,170 |
0,125 |
0,094 |
0,067 |
4,0 |
0,505 |
0,330 |
0,256 |
0,181 |
0,140 |
0,127 |
0,098 |
0,078 |
0,057 |
6,0 |
0,258 |
0,198 |
0,166 |
0,128 |
0,104 |
0,096 |
0,079 |
0,066 |
0,049 |
8,0 |
0,152 |
0,128 |
0,113 |
0,091 |
0,078 |
0,074 |
0,062 |
0,053 |
0,041 |
1,0 |
0,100 |
0,090 |
0,079 |
0,069 |
0,059 |
0,057 |
0,049 |
0,043 |
0,035 |
Колонну необходимо также проверить на возможность потери усточивости из плоскости действия изгибающего момента по формуле:
(6.22)
где
– коэффициент продольного изгиба
колонны в зависимости от условной
гибкости
.
(6.23)
Коэффициент вычисляется в cоответствии с пунктом 5.31 СНиП II-23-81.