
- •К.А. Вансович
- •Часть 2
- •Введение
- •Устойчивость магистральных трубопроводов
- •1.1. Потеря устойчивости прямого стержня под действием осевой сжимающей силы
- •1.2. Поперечные перемещения подземного участка магистрального трубопровода
- •1.3. Сопротивление грунта поперечным перемещениям трубы
- •1.4. Энергетический метод определения критической силы
- •1.5. Упрощенные зависимости для практических расчетов
- •1.5.1. Расчет на устойчивость прямолинейного участка трубопровода
- •1.5.2. Расчет на устойчивость изогнутого вверх участка трубопровода
- •2. Проектирование опор и эстакад магистральных и технологических трубопроводов
- •3. Железобетонные конструкции
- •3.1. Бетон
- •3.1.1. Прочность бетона
- •Кубический образец; b) кубический образец без трения;
- •3.1.2. Деформация бетона под нагрузкой
- •3.1.3. Классы и марки бетона.
- •3.2. Арматура
- •1) Бетонная балка; 2) стальная арматура; 3) трещины в растянутом бетоне
- •3.3. Арматурные изделия, закладные детали и стыки
- •3.4. Свойства железобетона
- •3.5. Методы расчета на прочность железобетонных конструкций
- •3.5.1. Сжатие прямого железобетонного элемента
- •3.5.2. Напряжения и деформации в железобетоне при растяжении
- •3.5.3. Напряжения и деформации в железобетонном элементе при изгибе
- •4. Конструирование и расчет отдельно стоящих опор.
- •4.1 Конструктивная схема шпальных отдельно стоящих опор.
- •4.2 Железобетонные опоры
- •4.3 Конструирование стальных опор
- •5. Расчет на прочность изгибаемых элементов отдельно стоящих опор
- •5.1 Нагрузки и воздействия на отдельно стоящие опоры
- •5.2 Расчет железобетонных траверс
- •5.2.1. Железобетонные траверсы с одиночной арматурой
- •5.2.2. Железобетонные траверсы с двойной арматурой
- •5.3 Расчет стальных балочных конструкций опор и эстакад.
- •5.3.1 Проверка двутавровой балки на прочность.
- •5.3.2 Сварные двутавровые балки
- •5.3.3 Проверка общей устойчивости балки
- •5.3.4 Проверка жесткости балок
- •5.3.5 Расчет поясных швов
- •5.3.6 Расчет сварных стыков двутавровых балок
- •6. Расчет элементов строительных конструкций на сжатие
- •6.1. Расчет центрально сжатых колонн
- •6.2. Расчет внецентренно сжатых колонн
- •6.3. Расчет базы колонны
- •7. Расчет отдельно стоящего фундамента под колонну
- •7.1. Определение размеров подошвы фундамента
- •46. Расчетная схема отдельного фундамента
- •Расчет отдельно стоящего центрально-сжатого фундамента на изгиб
- •7.3. Расчет отдельно стоящего фундамента на продавливание
- •7.4. Расчет внецентренно сжатого фундамента
- •8. Расчет продольных деформаций надземного участка трубопровода
- •9. Сферические резервуары
- •9.1. Определение напряжений в осесимметричных оболочках по безмоментной теории
- •9.2. Определение толщины стенки оболочки сферического резервуара
- •9.3. Кратковременные нагрузки на сферический резервуар
- •9.4. Деформации сферической оболочки
- •9.5. Расчет оболочки на устойчивость
- •9.6. Расчет стоек резервуара
- •– Стойка; 2) – оболочка; 3) – связи между опорами
- •Содержание
5.3.1 Проверка двутавровой балки на прочность.
Проверку на
прочность проводят в тех точках стальных
балок, где возникают наибольшие нормальные
или касательные напряжения. Кроме того,
рассматриваются те опасные места в
конструкции балки, где одновременно
действуют как нормальные, так и касательные
напряжения, так как именно в этих точках
может выполняться условие перехода
материала в пластическое состояние.
Как правило, в поперечных сечениях, где
возникают максимальный изгибающий
момент
![]() или максимальная поперечная (перерезывающая)
сила
или максимальная поперечная (перерезывающая)
сила
![]() приложены сосредоточенные силы от
нагрузок (например: от веса лежащей на
балке трубы), в том числе опорные реакции.
приложены сосредоточенные силы от
нагрузок (например: от веса лежащей на
балке трубы), в том числе опорные реакции.
В поперечных
сечениях балки, где изгибающий момент
![]() ,
проверку
на прочность выполняют по нормальным
напряжениям
,
проверку
на прочность выполняют по нормальным
напряжениям
![]() ,
(5.13)
,
(5.13)
где
![]() – момент сопротивления сечения нетто;
– момент сопротивления сечения нетто;
![]() – расчетное
сопротивление стали;
– расчетное
сопротивление стали;
![]() – коэффициент
условий работы.
– коэффициент
условий работы.
В тех случаях, когда в сечении с максимальным изгибающим моментом действуют еще и значительные поперечные силы, применяют следующую формулу (СНиП II-23-81)
![]() (5.14)
(5.14)
где
![]() – коэффициент, учитывающий возможность
развитие пластических деформаций.
– коэффициент, учитывающий возможность
развитие пластических деформаций.
Коэффициент вычисляют следующим образом.
Сначала вычисляют средние касательные напряжения в сечении
![]() (5.15)
(5.15)
где
![]() – толщина
стенки двутавра;
– толщина
стенки двутавра;
![]() – высота сечения
двутавра.
– высота сечения
двутавра.
Коэффициент
принимается равным
![]() по таблице 5.1, если касательные напряжения
по таблице 5.1, если касательные напряжения
![]() ,
где
,
где
![]() – расчетное сопротивление стали сдвигу.
– расчетное сопротивление стали сдвигу.
![]() ,
(5.16)
,
(5.16)
где
![]() – коэффициент надежности по материалу.
– коэффициент надежности по материалу.
Таблица 5.1
|
|
0,25 |
1,19 |
0,5 |
1,12 |
1,0 |
1,07 |
2,0 |
1,04 |
![]() – площадь полки
двутавра;
– площадь полки
двутавра;
![]() – площадь стенки
двутавра.
– площадь стенки
двутавра.
Для диапазона
![]() коэффициент
находят в зависимости от значения
средних касательных напряжений в сечении
коэффициент
находят в зависимости от значения
средних касательных напряжений в сечении
![]()
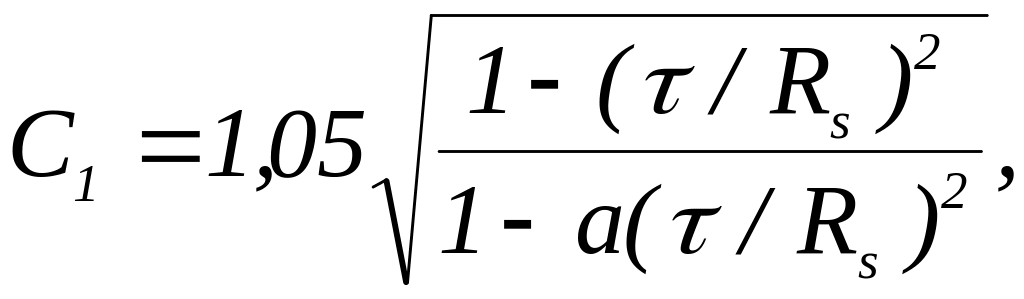 (5.17)
(5.17)
где
![]() – для двутавров, изгибаемых в плоскости
наибольшей жесткости;
– для двутавров, изгибаемых в плоскости
наибольшей жесткости;
![]() – для других
сечений.
– для других
сечений.
В сечения, где
возникает максимальная поперечная сила
![]() ,
проверка на прочность проводится по
касательным напряжениям (рис. 35).
,
проверка на прочность проводится по
касательным напряжениям (рис. 35).
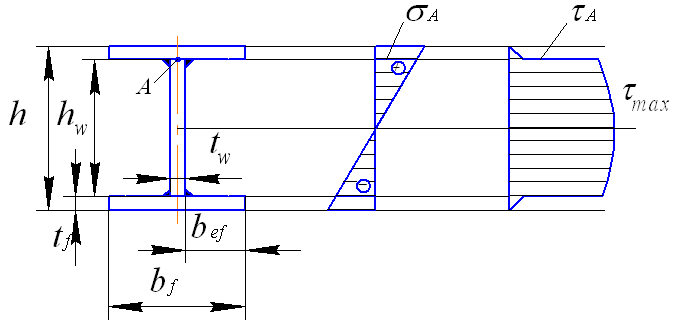
Рис.35. Расчетная схема изгиба стальной двутавровой балки
Для балки произвольного сечения касательные напряжения определяются по формуле Журавского
![]() ,
(5.18)
,
(5.18)
где
![]() – статический момент отсеченной части
сечения;
– статический момент отсеченной части
сечения;
![]() – момент инерции
сечения;
– момент инерции
сечения;
![]() – ширина сечения
в точке с координатой
– ширина сечения
в точке с координатой
![]() .
.
Для двутавра
максимальные касательные напряжения
возникнут на линии горизонтальной оси
симметрии, где
![]()
![]() .
(5.19)
.
(5.19)
Для тех сечений изгибаемых балок, где приложены сосредоточенные нагрузки, а также в опорных сечениях балок необходимо выполнить расчет на срез стенки двутавра
![]() (5.20)
(5.20)
где
![]() – высота стенки двутавровой балки.
– высота стенки двутавровой балки.
Для расчета на прочность балки в местах приложения нагрузки к верхнему поясу, а также в опорных сечениях балок, не укрепленных ребрами жесткости, следует выполнить проверку на прочность с учетом местных напряжений.
Величина местных
напряжений
![]() зависит
от нагрузки
зависит
от нагрузки
![]() ,
передающуюся от трубы через опорное
устройство, и размеров той площадки
стенки двутавра, на которую передается
деформация сжатия через изгибаемый
пояс двутавра (рис. 36)
,
передающуюся от трубы через опорное
устройство, и размеров той площадки
стенки двутавра, на которую передается
деформация сжатия через изгибаемый
пояс двутавра (рис. 36)
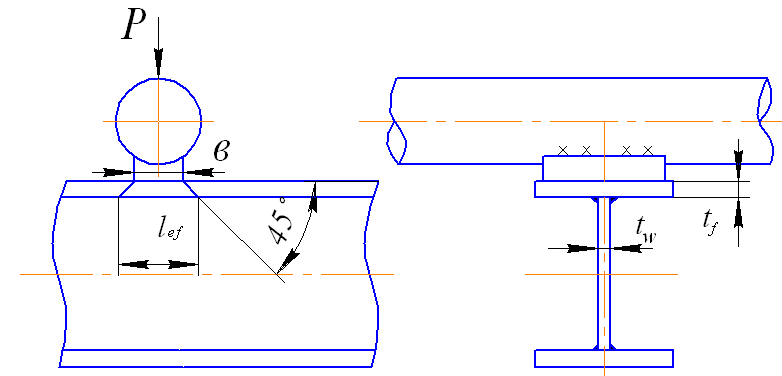
Рис.36. Расчетная схема двутавровой балки на изгиб в месте приложения нагрузки
Условие прочности при проверке только по местным напряжениям
![]() (5.21)
(5.21)
где – расчетное значение нагрузки (сосредоточенной силы);
![]() – условная
длина распределения локальной нагрузки
– условная
длина распределения локальной нагрузки
![]() .
(5.22)
.
(5.22)
