3.5.2. Напряжения и деформации в железобетоне при растяжении

При осевом растяжении железобетонных элементов различают три стадии нагружения, характеризуемых напряженно-деформированным состоянием.

На стадии 1 (рис. 24) в железобетонном элементе нет трещин, напряжения в бетоне .

Деформации бетона и арматуры равны по всей длине, т.к. сцепление между ними не нарушено

. (3.21)

Связь между деформациями и напряжениями в бетоне определяется диаграммой деформирования

, (3.22)

Напряжения в арматуре связаны с деформациями законом Гука

, (3.23)

С учетом того, что

, (3.24)

. (3.25)

По мере возрастания нагрузки напряжения в бетоне достигают предела прочности при растяжении _. На этом заканчивается стадия 1 и наступает стадия 2 – образование трещин в бетоне.

Напряжение в бетоне (конец стадии 1) достигает предела прочности на растяжение, а деформация становится равной

(3.26)

На основании обработки большого числа опытов предложено считать, что при растяжении коэффициент упругости бетона в момент разрушения =0,5.

Тогда деформации бетона

, (3.27)

а напряжение в арматуре

(3.28)

Усилие в момент появления трещин

. (3.29)

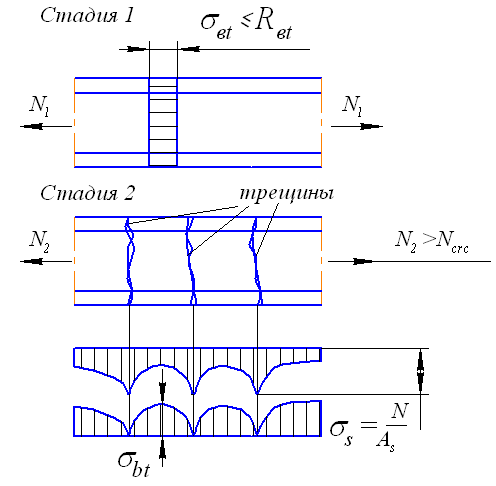
Рис. 24. Расчетная схема растягиваемого железобетонного элемента

На стадии 2, когда появляются трещины в бетоне, в сечениях, проходящих через эти трещины, сопротивление растяжению оказывает только арматура. В сечениях между трещинами сопротивление нагрузке оказывают и бетон и арматура, при этом по мере удаления от трещин напряжение в арматуре убывает, а в бетоне возрастает (рис. 24).

На стадии 3 напряжения в арматуре достигают предела прочности (временного сопротивления) и железобетонный элемент разрушается при усилии

. (3.30)

3.5.3. Напряжения и деформации в железобетонном элементе при изгибе

При изгибе железобетонной балки в зависимости от величины изгибающего момента в сечении последовательно возникают следующие стадии напряженно-деформированного состояния.

Стадия . При малых нагрузках напряжения в бетоне и арматуре малы. В бетоне возникают преимущественно упругие деформации. Эпюру напряжений, возникающих в сжатой и растянутой зонах изгибаемого элемента, можно изобразить почти прямой линией.

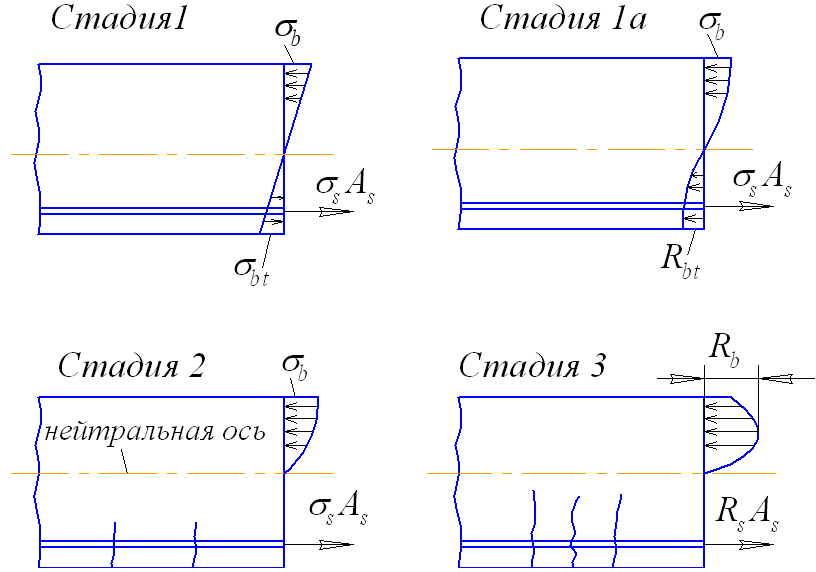
Рис.25. Расчетная схема изгибаемого железобетонного элемента

При увеличении нагрузки напряжения в бетоне и арматуре растут, в бетоне развиваются как упругие, так и неупругие деформации, эпюры напряжений искривляются, нейтральная ось балки перемещается в сторону сжатой области балки. Стадия характеризуется отсутствием трещин в растянутом бетоне и усилия воспринимаются всем сечением (при определении напряжений допускается применение зависимостей сопротивления упругих материалов).

Конечным этапом стадии является стадия , на которой напряжения бетона в растянутой зоне поперечного сечения балки достигают предела прочности на растяжение .

Стадия наступает с появлением трещин в растянутой зоне. В это время характерной является работа железобетона при наличии трещин. Напряжения в растянутой зоне бетона в сечениях, проходящих по трещине, принимаются равными нулю по всей высоте растянутой зоны.

Напряжения в сжатой зоне бетона на стадии остаются меньше предела прочности бетона , а в растянутой арматуре в начале они равны , а на конечном этапе в стадии достигают расчетного сопротивления арматуры растяжению .

Характер разрушения на стадии зависит от количества растянутой арматуры и ее механических свойств. Когда напряжения в арматуре достигают предела текучести происходит быстрое нарастание пластических деформаций и прогибов балки. В сжатой зоне бетона напряжения достигают предела прочности на сжатие и он начинает разрушаться. Наступает предельное состояние изгибаемого железобетонного элемента.