1.3.3. Определение осевых и центробежного моментов инерции сечения относительно центральных осей хc, уc
Находим моменты инерции “простых” фигур относительно собственных центральных осей. Сравнивая расположение фигур и осей на чертеже (рис. 1.5) и эскизах (рис. 1.4), замечаем, что
;
;
;
;
;
;
;
;
;
;
;
.
Знак центробежного момента инерции уголка в сечении определяем, представив интеграл по всей площади в виде суммы трёх подинтегралов (рис. 1.6):
.
Из рисунка видно, что первый и третий подынтегралы отрицательны и значительно превышают по модулю второй (положительный) подынтеграл. Следовательно, при данном расположении уголка его центробежный момент инерции отрицателен.
Вычисляем моменты инерции “простых” фигур относительно центральных осей ХC, YC всего сечения. Используем формулы для преобразования моментов инерции при параллельном переносе с центральных осей фигуры ХCi , YCi на параллельные им оси ХC , YC (рис. 1.5):
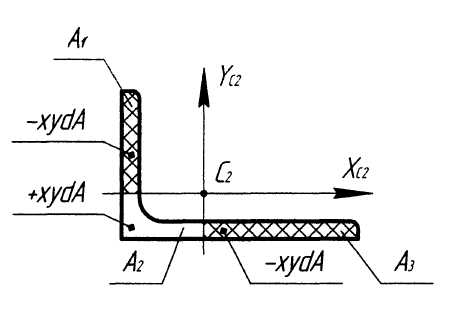
Рис 1.6. Определение знака центробежного момента инерции уголка
;
;
.
Для первой фигуры – двутавра:
;
;
.
Для второй фигуры – уголка:
;
;
.
Для третьей фигуры – листа:
;
;
.
Для четвёртой фигуры – швеллера :
;
;
.
Находим центральные моменты инерции поперечного сечения, произведя суммирование по всем составляющим фигурам:
1.3.4. Определение положения главных центральных осей
инерции сечения
Используем формулу (1.1):
.
Так как угол получился отрицательным, откладываем его по ходу часовой стрелки и проводим главные оси U и V (рис. 1.5).
Вычисляем значения тригонометрических функций
;
;
;
;
;
.
Проверяем основное тригонометрическое тождество
;
– верно.
1.3.5. Определение главных центральных моментов
инерции сечения
Используем формулы (1.2):
;
;
.
Проверяем правильность вычислений.
А. Условие стационарности суммы осевых моментов инерции при повороте осей:
JXC
+ JYC
= 4916+2602 =
7518
;
JU
+ JV
= 5624+1894
= 7518
– выполняется.
Б. Условие экстремальности главных осевых моментов инерции:
JU = 5624 > {JXC = 4916 ∩ JYC = 2602} – максимум ;
JV = 1894 < {JXC = 4916 ∩ JYC = 2602} – минимум .
В. Основное свойство
главных осей:
.
Выше мы вычислили
.
Относительная погрешность
|
⋍ |
0,03 %,
|
следовательно, условие выполняется. |
1.3.6. Определение моментов сопротивления относительно главных осей
Осевые моменты сопротивления характеризуют изгибную прочность стержней (балок) с заданными геометрическими параметрами сечения. Вычисляются они как отношения моментов инерции к расстояниям от главных осей до наиболее удаленных от них точек сечения. Чтобы найти опасные точки, проведём по две пары касательных, параллельных главным осям U, V (по разные стороны от осей), и выберем те точки касания, которые наиболее удалены от главных осей (устанавливаем визуально или с помощью линейки). В рассматриваемом примере от оси V наиболее удалена т. А, а от оси U – т. В (рис. 1.5).
Вычисляем главные координаты опасных точек, используя формулы аналитической геометрии:
;
,
где xA, yA, xB, yB, xC, yC – координаты точек А, В и центра тяжести C во вспомогательной системе координат XOY.
Из рис. 1.5 находим
;
;
;
.
В п. 1.3.2 мы вычислили хC = 8,86 см; уC = 19,33 см.
Подставляя в формулы эти значения, получаем
см;
см.
Знаки “минус” показывают, что точки удалены от главных осей в сторону отрицательного направления осей U и V.
Определяем осевые моменты сопротивления
;
.