5.3.3. Составление уравнений равновесия для заданной схемы рамы
Анализ предыдущего пункта показал, что для решения задачи одних уравнений равновесия недостаточно. Тем не менее рассмотрение их необходимо. Согласно рис. 5.5, а получаем
;
;
или
.
(5.10)
;
;
или
.
(5.11)
;
;
или
.
(5.12)
;
;
или
.
(5.13)
Составляем проверочное уравнение равновесия. Для данной схемы наиболее простым будет использование свойства внутреннего шарнира С
;
;
или
.
(5.14)
Если в раме
отсутствует внутренний шарнир, то в
качестве проверочного можно составить
любое уравнение, не используемое в
основной комбинации, например,
;
и т. д.
5.3.4. Выбор основной системы метода сил
Согласно п. 5.3.3
заданная рама имеет две “лишних” связи,
которые необходимо отбросить с целью
получения статически определимой
системы. Шарнирно-неподвижная опора В
имеет две
связи. Оставляем горизонтальную связь
для лучшего восприятия нагрузки
и удаляем вертикальную связь, превращая
внешний шарнир в вертикальный каток
(рис. 5.5, б).
Аналогично поступаем с шарнирно-неподвижной
опорой D
с той разницей, что для лучшего восприятия
внешнего момента М
оставляем вертикальную связь и удаляем
горизонтальную, превращая внешний
шарнир D
в горизонтальный каток (рис. 5.5, б).
Проверяем выполнение важнейших требований к основной системе – её статической определимости и кинематической неизменяемости:
,
.
Здесь
– число степеней свободы основной
системы;
(AC;
CBD)
– число дисков рамы, не имеющих глухих
заделок. Таким образом, выбранная
основная система статически определима
и кинематически неизменяема.
При рассмотрении других схем опирания рам можно произвести наряду с рассмотренными в примере следующие преобразования:
а) отбросить каток, удалив тем самым одну “лишнюю” связь;
б) глухую заделку заменить внешним шарниром, удалив тем самым одну “лишнюю” угловую связь;
в) глухую заделку заменить горизонтальным или вертикальным катком, удалив тем самым две связи: одну линейную (горизонтальную или вертикальную) и одну угловую;
г) отбросить шарнирно-неподвижную опору, удалив тем самым две “лишние” линейные связи;
д) врезать внутренний шарнир в каком-нибудь стержне рамы, удалив тем самым внутреннюю угловую связь, обеспечивающую восприятие изгибающего момента.
5.3.5. Рассмотрение грузового состояния основной системы
Это состояние
получаем, прикладывая к основной системе
заданные внешние нагрузки (рис. 5.5, в).
Основные опорные реакции обозначаем
,
,
и
,
а их направления оставляем такими же,
как и в заданной раме. Полагая в системе
уравнений (5.10) – (5.13)
;
,
получаем
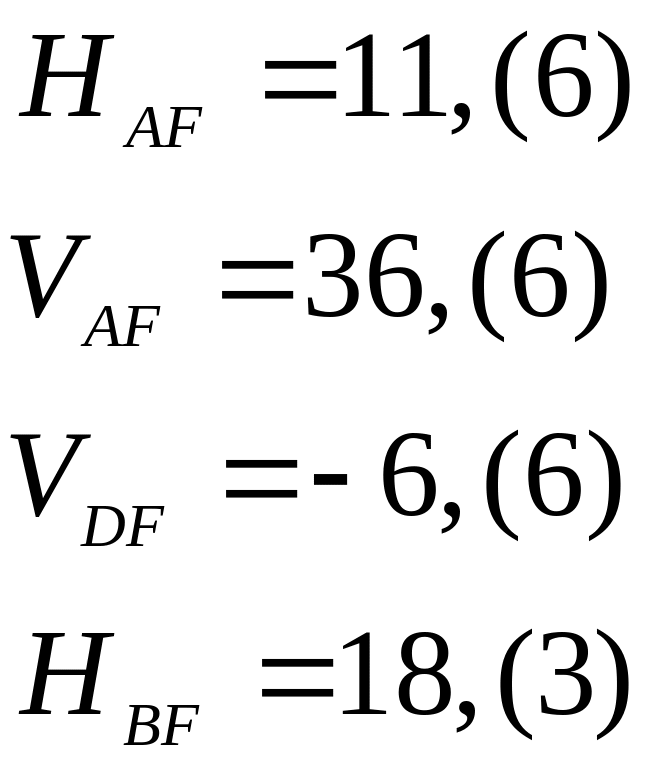
Проверяем выполнение уравнения (5.14):
;
;
.
Разбиваем стержни рамы на грузовые участки (аналогично балкам) и проводим текущие сечения i–i, привязывая их абсциссами к характерным узлам рамы (рис. 5.5, в). Составляем выражения изгибающих моментов относительно центров тяжестей сечений , рассматривая ту часть рамы, которая включает в себя соответствующую абсциссу . Правило знаков используем условное относительное, определяя для каждого участка положение сжатых волокон на вогнутой стороне упругой линии (геометрической оси стержня).
I
грузовой участок
– наклонная прямая
(0; 23,(3)) – сжатие волокон слева.
II
грузовой участок
– наклонная прямая
(23,(3); 6,(6)) – сжатие волокон слева.
III
грузовой участок
– квадратная
парабола (6,(6);23,(3); 0) – сжатие волокон
сверху.
IV
грузовой участок
– наклонная прямая
(20; 33,(3)) – сжатие волокон снизу.
V
грузовой участок
– квадратная
парабола (0; 8,(3); -3,(3)) – сжатие волокон
слева переходит в сжатие волокон справа
(произошла смена знака момента).
VI
грузовой участок
– наклонная прямая
(30; –13,(3)) – сжатие волокон слева переходит
в сжатие волокон справа.
VII
грузовой участок
– наклонная прямая
(–13,(3); 0) – сжатие волокон сверху.
По полученным данным строим грузовую эпюру изгибающих моментов (рис. 5.5, г), откладывая с удобным масштабным коэффициентом со стороны сжатых волокон стержней характерные значения моментов, взятые по модулю, т. е. без учёта знаков. Чтобы обнаружить возможные ошибки в расчётах и неправильное определение сжатых волокон, производим статическую проверку равновесия узлов рамы. Мысленно вырезаем узлы бесконечно близко к их геометрическим центрам и прикладываем в сечениях моменты, взятые с эпюры и направленные в сторону эпюры, обеспечивая тем самым положение сжатых волокон, (рис. 5.6):
-
;
;
.
;
;.
;
;.
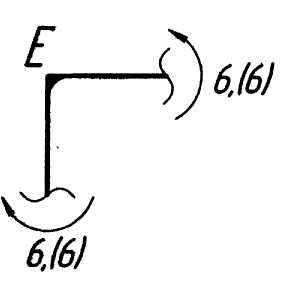
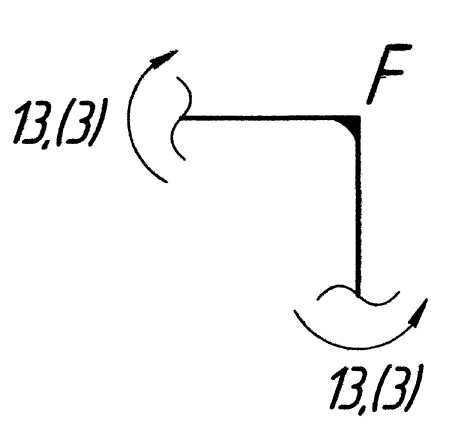
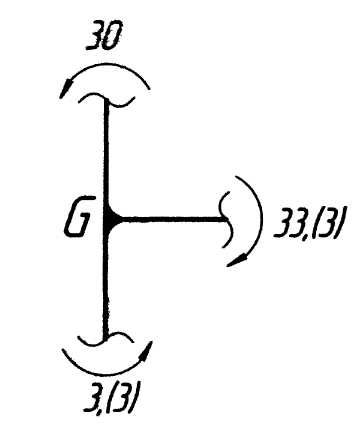
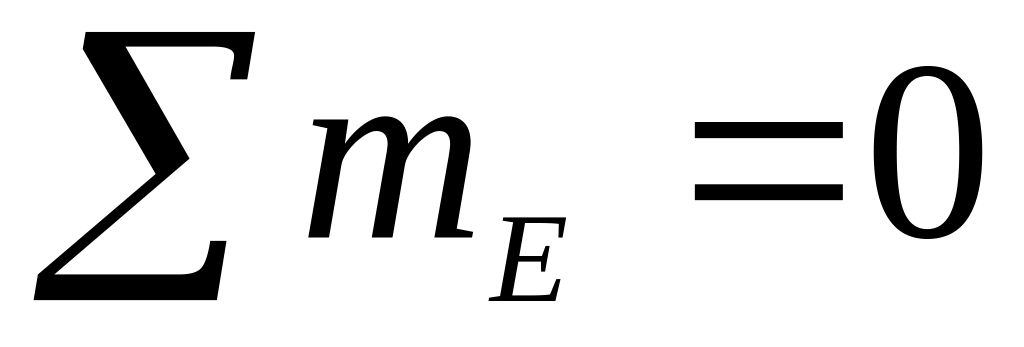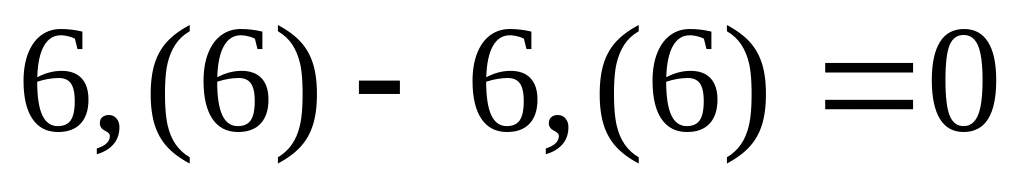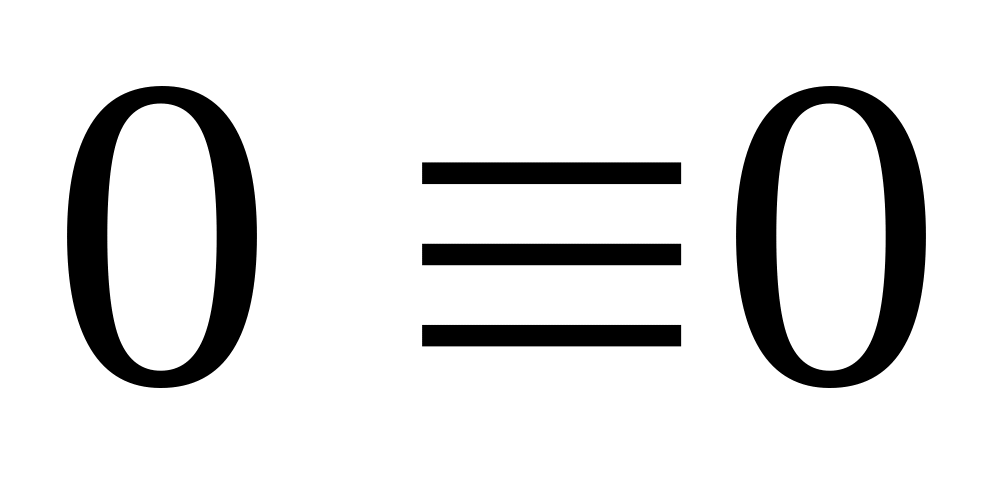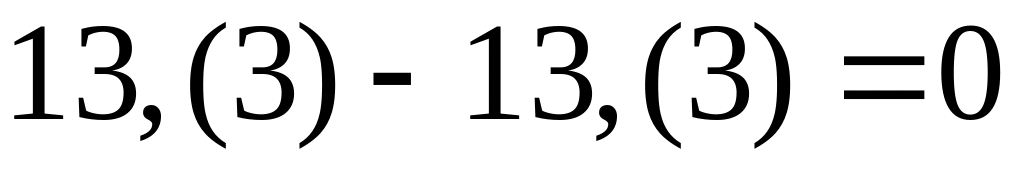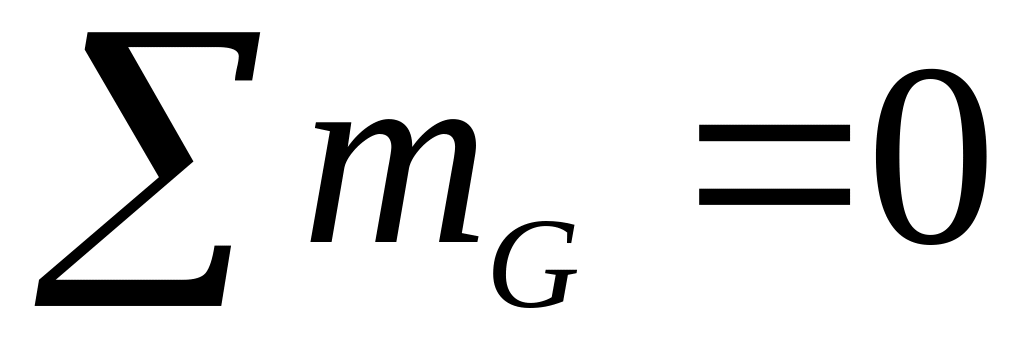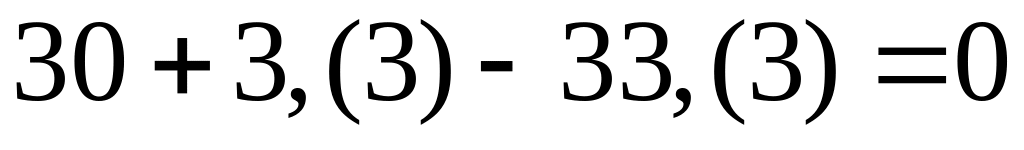Рис. 5.6. Статическая проверка эпюры
Как видно из составленных уравнений, все характерные узлы находятся в равновесии. Если в некотором узле рамы приложен сосредоточенный внешний момент М, то при составлении уравнения равновесия данного узла этот момент также необходимо учесть.