3.3.4. Определение реакций в шарнирно сочленённой балке

Схему этой балки получаем из предыдущей консольной балки, восстановив шарнирно-подвижную опору в т. В и врезав внутренний шарнир в произвольной т. С, принадлежащей отрезку АВ (рис. 3.6).

В этой схеме опирания балки неизвестными являются реакции , и реактивный момент . Для их определения составляем три уравнения равновесия всей балки или её сочленённых частей.

Приравниваем к нулю сумму моментов относительно т. С всех сил, расположенных справа от шарнира:

; ;

, отсюда находим

кН.

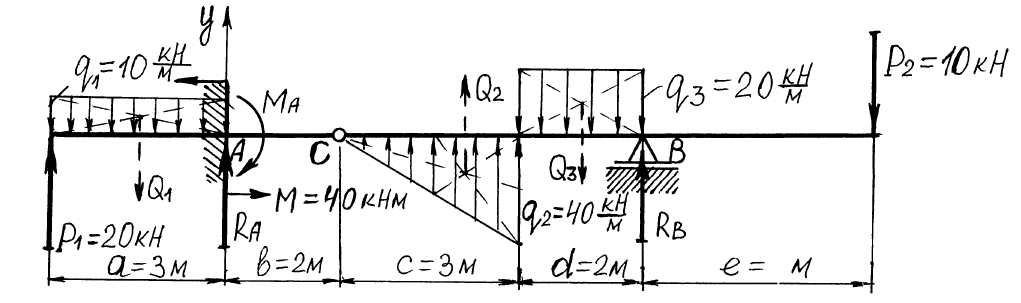
Рис. 3.6. Расчётная схема шарнирно-сочленённой балки

Приравниваем к нулю сумму моментов всех сил относительно т. А:

;

;

, отсюда находим .

Приравниваем к нулю сумму моментов относительно т. С всех сил, расположенных слева от шарнира:

; ;

, отсюда находим

кН.

Проверяем правильность вычислений, приравнивая к нулю сумму проекций всех сил на ось Y:

; ;

; .

3.3.5. Построение эпюр поперечных сил и изгибающих моментов

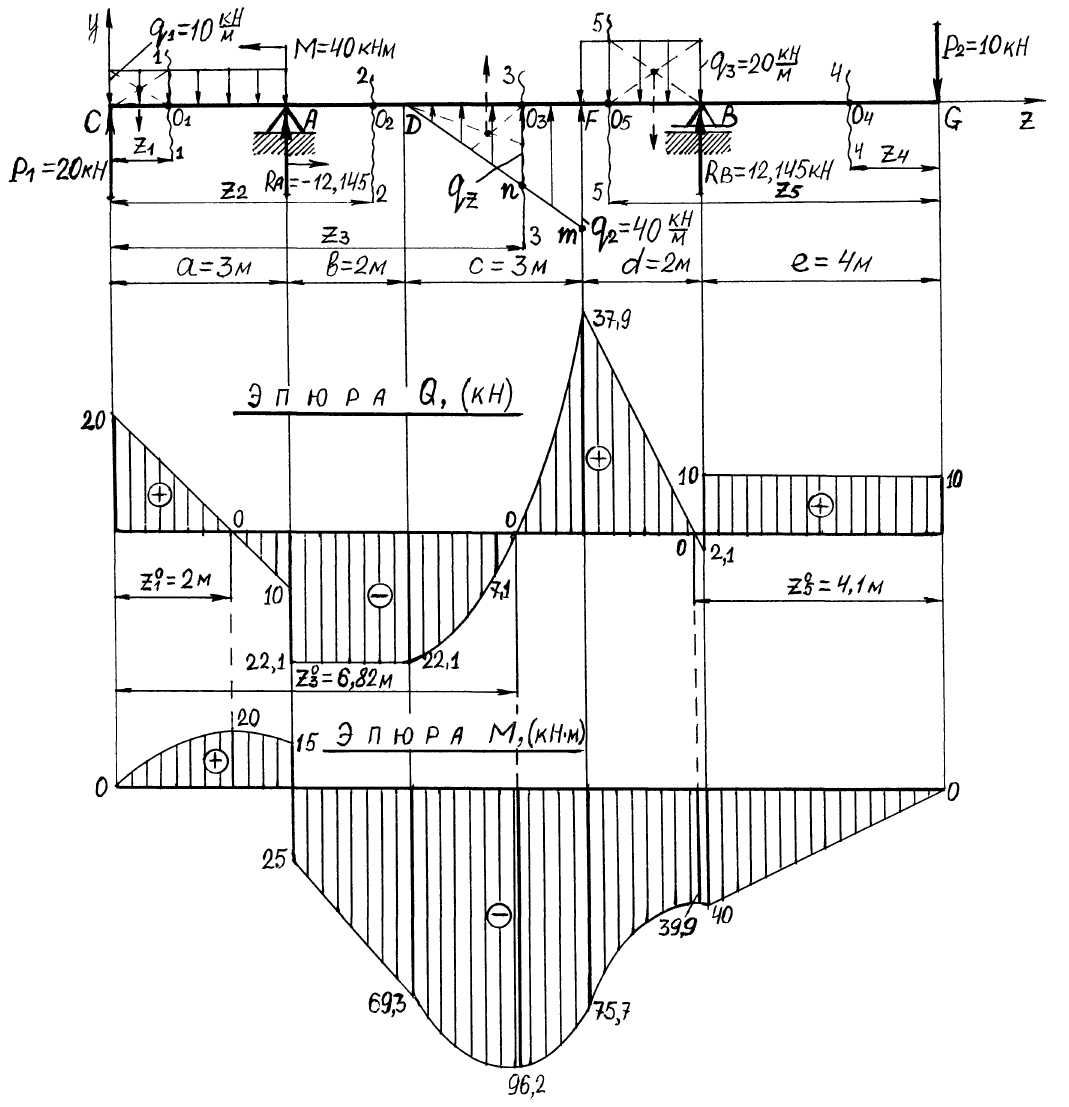
Названные эпюры строим для балки с двумя шарнирными опорами, т. е. для случая, рассмотренного в п. 3.3.2. Расчётная схема для построения эпюр внутренних усилий показана на рис. 3.7, а. Прежде всего, разбиваем длину балки на грузовые участки, т. е. такие отрезки, в пределах которых остаётся постоянным характер нагружения. В рассматриваемом примере получаем пять участков: CA, AD, DF, FB, BG.

В пределах каждого участка проводим текущее сечение i–i (i = 1, 2, 3, …) и привязываем его абсциссой z_i к началу или концу балки в зависимости от сложности учёта нагрузок, расположенных на отсечённой части балки длиной z_i . Трудоёмкость вычислений можно оценить по следующей формуле:

,

где – коэффициент сложности i-го вида нагрузки; – число нагрузок i-го вида.

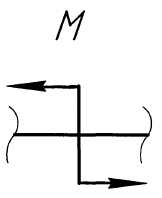
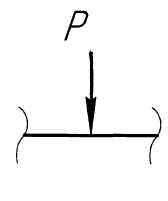
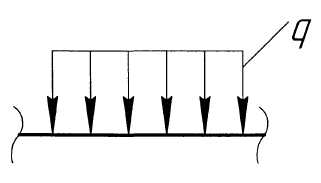
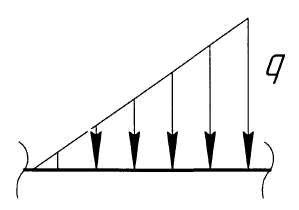
Вид нагрузки
Коэффициент сложности	1	3	5	7	12

Например, если для сечения 3–3 (рис. 3.7, а) рассматривать левую отсечённую часть , то сложность расчёта составит . Если рассматривать правую отсечённую часть , то сложность . Так как , то сечение 3–3 легче рассчитать слева, чем справа. Исходя из высказанных соображений, в данном примере будем рассматривать сечения 1–1, 2–2,

3–3 слева, а сечения 4–4, 5–5 справа (рис. 3.7, а).

Используя определения поперечной силы (3.1) и изгибающего момента (3.2), а также их правила знаков, записываем выражения внутренних усилий для каждого грузового участка, анализируем характер их изменения по длине и вычисляем те значения, по которым можно построить графики функций (эпюры Q и М):

I грузовой участок са

; графиком этой функции является наклонная прямая, которую можно построить по двум точкам – в начале (т. С) и в конце (т. А) грузового участка: кН; кН. Так как функция меняет знак, то она принимает в некоторой точке участка нулевое значение. Вычисляем абсциссу этой точки ;

;  (0; 3);  ;

графиком этой функции является квадратная парабола, которую можно построить по трём точкам – в начале (т. С), в нулевой точке эпюры и в конце (т. А) грузового участка: ; ; . Замечаем, что при изгибающий момент принимает экстремальное значение на участке СА, так как 20 > (0; 15), что согласуется с дифференциальными проверками (3.4).

а)
б)
в)

Рис. 3.7. Расчётная схема балки. Эпюры поперечных сил и изгибающих моментов