3.2. Условие задания
Для данной схемы балки необходимо:
1. Определить реакции для трёх случаев опирания:
а) в шарнирно опёртой балке согласно исходной предпосылке;
б) в консольной балке с жёстким защемлением (глухой заделкой) в т. А при отсутствии опоры в т. В;
в) в шарнирно сочленённой балке с глухой заделкой в т. А, подвижной опорой в т. В и внутренним шарниром в т. С(А, В).
2. Построить эпюры поперечных сил и изгибающих моментов для шарнирно опёртой балки.
3. Подобрать размеры
поперечных сечений различной формы из
условия прочности по нормальным
напряжениям при
.
4. Провести анализ экономичности принятых видов сечений.
3.3. Пример расчёта и методические указания
3.3.1. Подготовка исходных данных и расчётной схемы балки
Решение задачи начинаем с выбора исходных данных из табл. 3.1 и 3.2. В качестве примера рассмотрим следующие данные.
Длина балки
.
Точки опирания и
приложения нагрузок: NA
= 3; NB
= 10;
=
3;
=
0;
=
14;
=
0;
=
3;
=
5;
=
8;
=
8;
=
10.
Числовые значения
внешних нагрузок: М = 40
;
= 20
кН;
= –10
кН;
=
–10 кН/м;
=
40 кН/м;
=
–20 кН/м.
Используя исходные данные, изображаем расчётную схему. Длину балки чертим в масштабе М 1: 50 (в 2 см схемы – 1 м длины балки). Так как табличные значения , и имеют знак “–”, то направляем эти нагрузки вниз (см. примечание к табл. 3.2). Длины участков (а, в, с,…) находим из геометрических соображений. Для рассматриваемого примера расчётная схема балки показана на рис. 3.4.
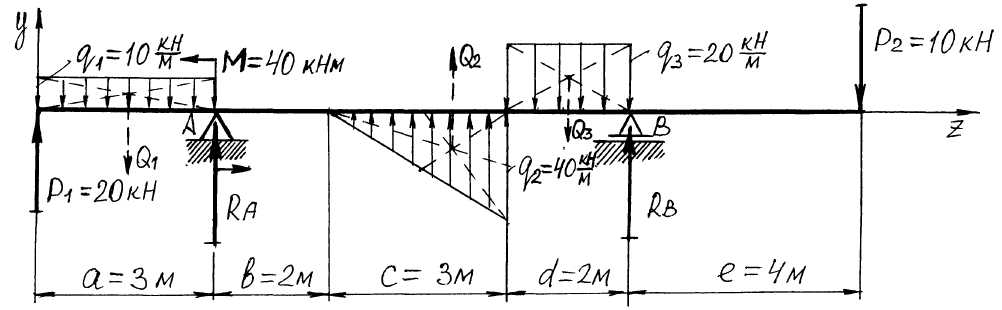
Рис. 3.4. Расчетная схема шарнирно опёртой балки
3.3.2. Определение реакций в шарнирно-опёртой балке
Показываем опорные
реакции
и
в точках А и
В.
Так как все активные нагрузки вертикальны,
то горизонтальная составляющая
в шарнирно-неподвижной опоре А
будет заведомо равна нулю и поэтому на
рис. 3.2 не показана. Распределённые
нагрузки
,
,
заменяем их равнодействующими
,
,
,
приложенными в центрах тяжестей
прямоугольников (на пересечении
диагоналей) и треугольника (на пересечении
медиан).
Для определения
реакций
и
составляем два уравнения равновесия
балки, предварительно вычислив значения
равнодействующих
кН;
кН;
кН.
Приравниваем к нулю сумму моментов всех сил относительно т. В:
;
;
,
отсюда находим
кН.
Приравниваем к нулю сумму моментов всех сил относительно т. А:
;
;
;
отсюда находим
кН.
Выполняем проверку правильности вычислений реакций, приравнивая к нулю сумму проекций всех сил на ось Y:
;
;
;
92,145 – 92,145 ≡
0.
В связи с приближённостью вычислений довольно часто тождество не выполняется абсолютно, а возникает некоторая ошибка, допустимость которой оценивают величиной относительной погрешности
,
где
и
– соответственно сумма положительных
и отрицательных слагаемых в уравнении
равновесия.
Если погрешность превышает допустимую величину, то необходимо исправить ошибки или увеличить число значащих цифр при вычислениях.
3.3.3. Определение реакций в консольной балке
Заменяем способ опирания балки, рассмотренной выше. Вместо шарнирно-неподвижной опоры А вводим глухую заделку, а шарнирно-подвижную опору В отбрасываем. В результате получаем консольную балку, показанную на рис. 3.5.
В заделке возникает
вертикальная реакция
и реактивный момент
.
Для их определения также составляем
два уравнения равновесия. Приравниваем
к нулю сумму проекций всех сил на ось
Y:
;
;
,
отсюда находим
.
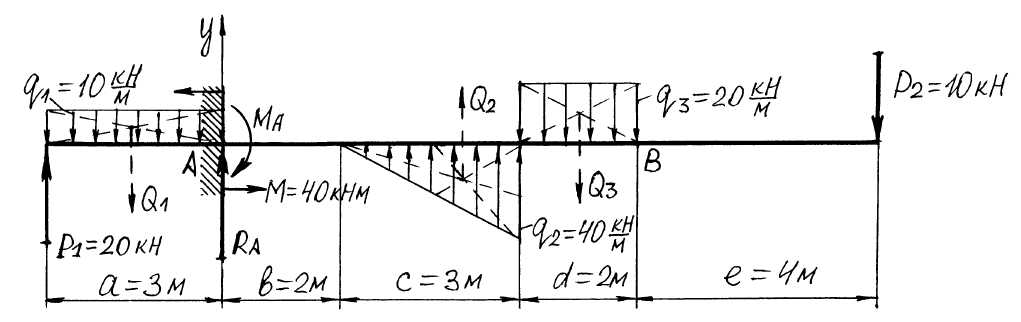
Рис. 3.5. Расчетная схема консольной балки
Приравниваем к нулю сумму моментов всех сил относительно т. А:
;
;
,
отсюда находим
.
Выполняем проверку, приравнивая к нулю сумму моментов всех сил относительно т. В:
;
;
.
Относительная погрешность вычислений
≃0,04
% < 0,2 %.