3. Плоский изгиб балок
Плоский изгиб
балок является одним из наиболее опасных
случаев нагружения деталей машин и
элементов сооружений, когда силовая
плоскость проходит через одну из главных
центральных осей инерции сечения (см.
гл. 1).
При плоском поперечном изгибе (в
дальнейшем просто “изгибе”) в сечении
балки возникают два внутренних усилия:
поперечная сила
и изгибающий момент
,
расположенные в силовой плоскости YOZ.
Поперечная сила
в произвольном сечении балки равна
алгебраической сумме проекций на
вертикальную ось Y
всех внешних нагрузок, расположенных
по одну сторону от рассматриваемого
сечения, т. е.
.
Поскольку все нагрузки
параллельны оси Y
и пары сил
не дают проекций на оси, определение
поперечной силы можно упростить, полагая,
что она равна алгебраической сумме
нагрузок (кроме пар сил), расположенных
по одну сторону от сечения, т. е.
.
(3.1)
При вычислениях используют следующее правило знаков (рис. 3.1):
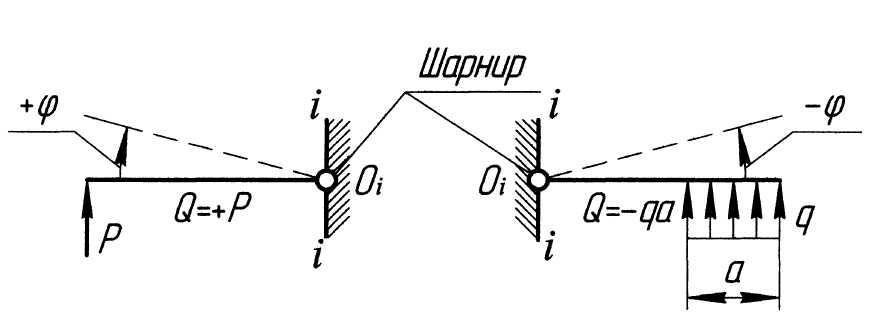
Рис. 3.1. Правило знаков для поперечной силы
внешняя нагрузка,
вращающая отсечённый элемент балки
(шарнирно закреплённый в центре тяжести
сечения
)
по ходу часовой стрелки, создаёт
положительную поперечную силу, а против
часовой стрелки –отрицательную.
Изгибающий момент
в произвольном сечении балки равен
алгебраической сумме моментов относительно
горизонтальной оси X
всех внешних нагрузок, расположенных
по одну сторону от рассматриваемого
сечения, т. е.
.
Учитывая расположение нагрузок,
определение изгибающего момента можно
упростить, полагая, что он равен
алгебраической сумме моментов отсечённых
нагрузок относительно центра тяжести
сечения, т. е.
.
(3.2)
При вычислениях используют следующее правило знаков (рис. 3.2):
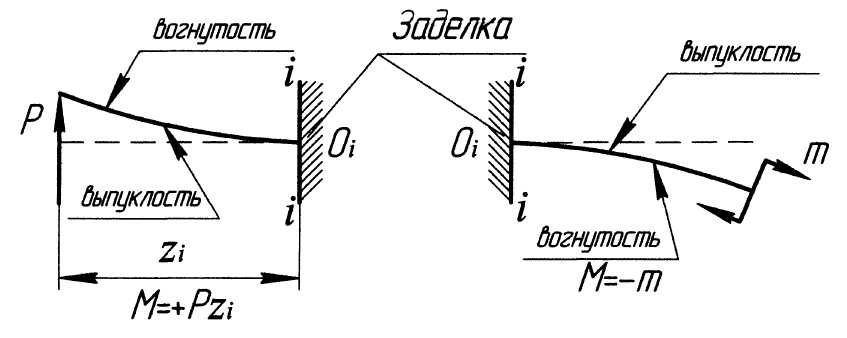
Рис. 3.2. Правило знаков для изгибающего момента
внешняя нагрузка, искривляющая отсечённый элемент балки (жёстко защемленный в рассматриваемом сечении i–i) выпуклостью вниз, создаёт положительный изгибающий момент, а выпуклостью вверх –отрицательный.
С целью определения наиболее опасных сечений строят эпюры поперечных сил и изгибающих моментов по длине балки. Для проверки правильности построения эпюр используют третий закон Ньютона (действие равно противодействию) и дифференциальные зависимости между внутренними усилиями Q, M и интенсивностью распределённой нагрузки q.
Ньютоновские проверки выполняют для каждой границы между грузовыми участками, где наблюдается изменение характера нагружения, например приложены сила или момент, начинается или заканчивается распределённая нагрузка и др. Эти проверки заключаются в выполнении условий
;
,
(3.3)
где
– разрыв функции I
рода (скачок);
и
– поперечная сила справа и слева от
границы k;
и
– изгибающий момент справа и слева от
границы k;
– внешняя сосредоточенная сила на k-й
границе;
– внешний сосредоточенный момент на
k-й
границе.
Дифференциальные проверки должны выполняться для всех сечений балки. Обычно они записываются в виде
(3.4)
где d
– дифференциал; z
– абсцисса сечения (аргумент);
,
,
– функции,
характеризующие изменение по длине
балки распределённой нагрузки, поперечной
силы и изгибающего момента.
Полезно помнить, что геометрический смысл первой производной – это тангенс угла наклона касательной к графику функции, а второй производной – кривизна функции в рассматриваемой точке. Угол наклона положителен, если он образован поворотом оси Z против часовой стрелки; кривизна положительна, если имеет выпуклость внизу; распределённая нагрузка положительна, если направлена вверх.
Третий вид проверок
– это интегральные зависимости между
функциями
,
и приращениями функций
и
,
которые они получают в пределах каждого
грузового участка
(3.5)
Здесь
– приращение функции; а,
b
– абсциссы начала и конца грузового
участка.
Полезно помнить, что приращение функции – это число, а интегралы в правой части – это площади, ограниченные графиком функции и осью Z в пределах грузового участка.
При изгибе балки
в точках её поперечных сечений появляются
два вида напряжений: нормальные
и касательные
.
Нормальные напряжения, играющие решающую
роль при разрушении балок, создаются
изгибающим моментом и определяются по
формуле
где
– изгибающий момент в рассматриваемом
сечении; 
–
осевой момент инерции относительно
главной центральной оси X;
y –расстояние
от оси X
до точки, в которой определяется
напряжение; знак
“–” в правой части объясняется тем, что при положительных значениях М и y появляются сжимающие напряжения , которые считаются отрицательными.
Касательные напряжения имеют второстепенное значение при расчётах балок на прочность, так как сравнительно редко являются причиной разрушения. Эти напряжения зависят от поперечной силы и определяются по формуле Д.И. Журавского:
-
,
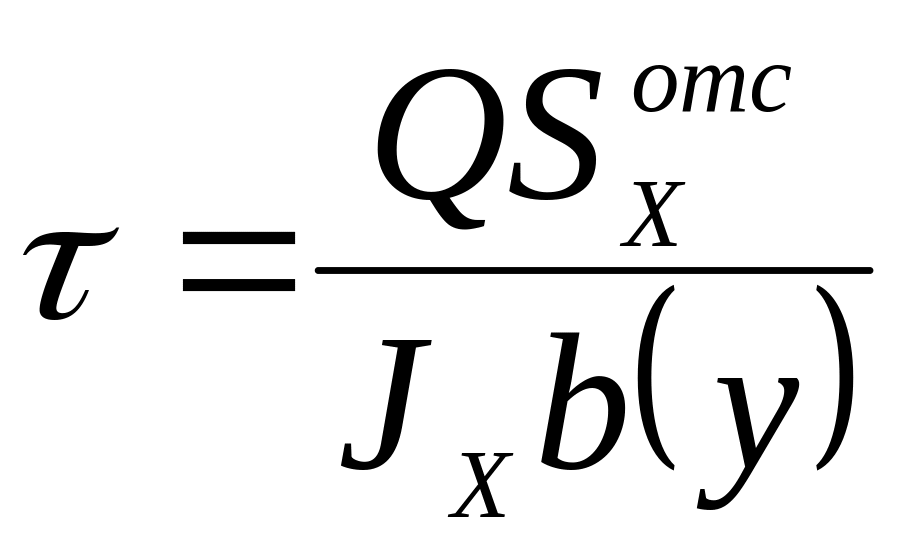
где
– поперечная сила в рассматриваемом
сечении;
– статический момент площади сечения,
расположенной по одну сторону от
исследуемой точки;
– осевой момент инерции; b(
y)
– ширина сечения на расстоянии y
от центральной оси X.
С учётом вышесказанного расчёт балок выполняют, исходя из условия прочности по нормальным напряжениям
(3.6)
где
– наибольший по модулю изгибающий
момент, возникающий в балке;
– осевой момент сопротивления поперечного
сечения;
– допускаемые напряжения при растяжении
или сжатии.
При проектировочном
расчёте балок на прочность, когда
известны внешние нагрузки, типы опор,
длина и материал балки, строят эпюру
изгибающих моментов
и задаются формой поперечного сечения
.
По эпюре
находят
,
а по форме сечения выражают
через характерный размер сечения а.
Используя условие прочности, находят
параметр а,
решив соответствующее кубическое
уравнение
