
Диффузия связанного электрона в энергетическом пространстве; ударно-радиационная рекомбинация
Поскольку энергии частиц в низкотемпературной плазме значительно ниже потенциалов возбуждения и ионизации, то ступенчатые процессы ионизации и рекомбинации преобладают над рассмотренными в предыдущих разделах прямыми процессами. Иными словами, ионизация имеет место большей частью из возбужденных состояний, а скорость рекомбинации связана со скоростью распада возбужденных состояний. Во всех этих процессах важную роль играют высоко возбужденные состояния и величина скорости их релаксации при столкновениях с другими частицами.
При столкновениях атомов, находящихся в верхних возбужденных состояниях, со свободными электронами наиболее вероятны переходы связанного электрона на близлежащие уровни. Поскольку плотность ридберговских уровней очень высока, то хорошим приближением является модель диффузии связанного электрона в квазинепрерывном энергетическом пространстве связанных состояний. В соответствии со стандартным определением диффузии в обычном пространстве
 (8.32)
можно ввести коэффициент диффузии в
энергетическом пространстве
(8.32)
можно ввести коэффициент диффузии в
энергетическом пространстве
 .
(8.33)
.
(8.33)
При рекомбинации электрон захватывается на один из верхних уровней с энергией связи (k ~ Te). Поскольку время жизни ридберговских состояний очень велико, сечение столкновительных переходов большое, то связанный электрон под действием соударений блуждает по верхним уровням. В результате блужданий он может перейти в континуум (процесс завершится ионизацией), либо полностью потерять энергию, когда атом переходит в основное состояние. В этом случае рекомбинацию можно считать состоявшейся. Для случая столкновений атома со свободными электронами коэффициент диффузии связанного электрона был получен Гуревичем. Он имеет вид
 ,
(8.34) где
,
(8.34) где
 – кулоновский логарифм для связанного
электрона. Если возбужденный атом
сталкивается с атомами, то
– кулоновский логарифм для связанного
электрона. Если возбужденный атом
сталкивается с атомами, то
 .
(8.35)
.
(8.35)
Рассмотрим плазму, состоящую из ионов (ni), тяжелых частиц (nа), и электронов (nе) со средней энергией = (3Те/2). В общем случае эта плазма не равновесна. Запишем уравнение изменения концентрации электронов
 ,
(8.36) где
,
(8.36) где
 – поток электронов через границу
ионизации в пространстве энергий. Здесь
k
– дискретные состояния, индекс q
– тип элементарного процесса,
Fe
и
Ge
– источники и стоки электронов за счет
процессов, не входящих в сумму
(диффузионные потоки, ионизация примесей,
включение внешнего ионизатора). Чтобы
решить уравнение (8.36), населенности nk
находим из уравнения баланса
– поток электронов через границу
ионизации в пространстве энергий. Здесь
k
– дискретные состояния, индекс q
– тип элементарного процесса,
Fe
и
Ge
– источники и стоки электронов за счет
процессов, не входящих в сумму
(диффузионные потоки, ионизация примесей,
включение внешнего ионизатора). Чтобы
решить уравнение (8.36), населенности nk
находим из уравнения баланса
 .
(8.37) В квазистационарном
приближении эта система алгебраическая.
Решив ее и подставив в уравнение (8.36),
получим
.
(8.37) В квазистационарном
приближении эта система алгебраическая.
Решив ее и подставив в уравнение (8.36),
получим
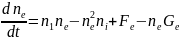 .
(8.38) Данное выражение для
суммы всех процессов носит совершенно
иной смысл, чем выражения, записанные
для элементарных процессов. В частности,
коэффициенты
ионизации и
рекомбинации в данном случае не связаны
соотношением детального равновесия;
определена
формально как константа второго порядка
(см3/с),
а
–
третьего (см6/с).
Соотношение между
и
носит
не термодинамический, а кинетический
характер и зависит от отношений
вероятностей элементарных процессов.
Выражение
.
(8.38) Данное выражение для
суммы всех процессов носит совершенно
иной смысл, чем выражения, записанные
для элементарных процессов. В частности,
коэффициенты
ионизации и
рекомбинации в данном случае не связаны
соотношением детального равновесия;
определена
формально как константа второго порядка
(см3/с),
а
–
третьего (см6/с).
Соотношение между
и
носит
не термодинамический, а кинетический
характер и зависит от отношений
вероятностей элементарных процессов.
Выражение
 означает, что при таком определении
и
только атомы в основном состоянии
считаются реагентами и продуктами, а
все остальные состояния рассматриваются
как промежуточные.
означает, что при таком определении
и
только атомы в основном состоянии
считаются реагентами и продуктами, а
все остальные состояния рассматриваются
как промежуточные.
В
квазистационарном приближении, когда
 и
и
 ,
имеем
,
имеем
 ,
(8.39) Если
,
(8.39) Если
 ,
имеем режим ионизации; если
,
имеем режим ионизации; если
 ,
– рекомбинации. При
,
– рекомбинации. При
 имеем квазистационарное состояние, но
не обязательно равновесие, так как
ионизация и рекомбинация могут
осуществляться разными процессами.
Полное описание процессов в плазме
возможно в рамках представления о
диффузии электронов в энергетическом
пространстве. Оно описывается уравнением
Фоккера-Планка
имеем квазистационарное состояние, но
не обязательно равновесие, так как
ионизация и рекомбинация могут
осуществляться разными процессами.
Полное описание процессов в плазме
возможно в рамках представления о
диффузии электронов в энергетическом
пространстве. Оно описывается уравнением
Фоккера-Планка
 ,
(8.40) где
,
(8.40) где
 – коэффициент динамического трения,
– коэффициент динамического трения,
 –
коэффициент диффузии. Так как поток
–
коэффициент диффузии. Так как поток
 (8.41)
должен обращаться в нуль при равновесии,
можно записать
(8.41)
должен обращаться в нуль при равновесии,
можно записать
 .
(8.42) Введя
обозначение
.
(8.42) Введя
обозначение
 ,
из уравнений (8.40) и (8.42) найдем
,
из уравнений (8.40) и (8.42) найдем
 .
(8.43) И так задача
нахождения
и
сводится к решению уравнения (8.40). В
условиях квазистационарности dn/dt
= 0
и j
= const.
Тогда при столкновениях связанного
(ридберговского) электрона со свободным,
используя уравнение (8.34), получим
коэффициент ударной рекомбинации
.
(8.43) И так задача
нахождения
и
сводится к решению уравнения (8.40). В
условиях квазистационарности dn/dt
= 0
и j
= const.
Тогда при столкновениях связанного
(ридберговского) электрона со свободным,
используя уравнение (8.34), получим
коэффициент ударной рекомбинации
 .
(8.44) Аналогично,
используя диффузионное приближение
для трехчастичной (с участием атома)
рекомбинации, получим
.
(8.44) Аналогично,
используя диффузионное приближение
для трехчастичной (с участием атома)
рекомбинации, получим
 .
(8.45) Те же
функциональные зависимости мы получили
из формулы Томсона, но теперь имеем
числовые коэффициенты.
.
(8.45) Те же
функциональные зависимости мы получили
из формулы Томсона, но теперь имеем
числовые коэффициенты.
