4.2. Непараметрические показатели связи
При
изучении нелинейной связи между
величинами в совокупностях, распределение
которых не соответствует нормальному
типу, более эффективны непараметрические
показатели связи. Они основаны на замене
наблюдаемых величин рангами. Статистическая
программа STATISTICA
оценивает непараметрические критерии
зависимости между переменными: статистика
Спирмена (коэффициент ранговой корреляции
Спирмена (
));
коэффициент конкордации Кендела (t);
коэффициент Гамма (γ).
Методика расчета коэффициент ранговой корреляции Спирмена ( )
Пример 1. Переменная NCOR1 содержит значения усвояемости (оцененных по методу L.Хантера) засилосованной массы 9 различных культур, а переменная NCOR2- их оценки по 6 балльной шкале. Предполагается, что метод Хантера положительно связан с бальной оценкой.
NCOR1: 44,4 45,9 41,9 53,3 44,7 44,1 50,7 45,2 60,1
NCOR2: 2,6 3,1 2,5 5 3 6 5,2 2,8 3,8
Необходимо подтвердить или опровергнуть это предположение.
Методика расчета коэффициента корреляции Спирмена ( )
Таблица 17
Расчет коэффициента корреляции Спирмена ( )
Х |
У |
Rх |
Rу |
Rx-Ry |
(Rx-Ry)² |
44,4 |
2,6 |
7 |
8 |
-1 |
1 |
45,9 |
3,1 |
4 |
5 |
-1 |
1 |
41,9 |
2,5 |
9 |
9 |
0 |
0 |
53,3 |
5 |
2 |
3 |
-1 |
1 |
44,7 |
3 |
6 |
6 |
0 |
0 |
44,1 |
6 |
8 |
1 |
7 |
49 |
50,7 |
5,2 |
3 |
2 |
1 |
1 |
45,2 |
2,8 |
5 |
7 |
-2 |
4 |
60,1 |
3,8 |
1 |
4 |
-3 |
9 |
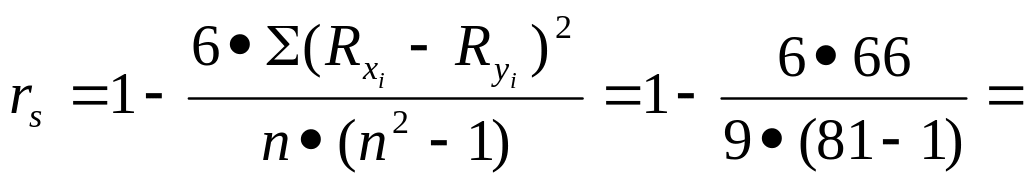0,45
1,33
Порядок выполнения.
После выбора значений из таблицы данных на основе графика рассеяния определяют тип связи. Между значениями установлена нелинейная связь. Величина связи определяется на основе непараметрического критерии зависимости между переменными коэффициента ранговой корреляции Спирмена ( ).
Результаты. Спирмeн=0,45, Z=1,33, значимость=0,22>0,05 (Рис.38), число степеней свободы = 9. Принимается нулевая гипотеза, нет корреляции между выборками.
Заключение. Статистическая программа оценивает нелинейную связь на основе коэффициента корреляции Спирмена. Проверка производится на основе сравнения фактического значения коэффициента корреляции Спирмена =0,45 с критическим значением rкрит.=0,6 (табл.18).
Эмпирическое значение меньше критического. Принимается нулевая гипотеза. В генеральной совокупности связь между оцениваемыми величинами отсутствует. Проверку нулевой гипотезы статистическая программа производит и на основе Z-статистики, установления ее уровня значимости. Z-статистика составляет 1,33; ее уровень значимости равен 0,224, больше 0,05. Нулевая гипотеза принимается; нет связи между оцениваемыми величинами в генеральной совокупности. При наличии среди оцениваемых переменных порядковых переменных (или качественных признаков) определяется коэффицицент тау Кендала (t). Если переменные содержат много повторяющихся значений оценка зависимости производится на основе коэффициента гамма (γ).
Результаты оценки показывают зависимость между засилосованными культурами и их балльной оценкой: коэффициент тау Кендала t=0,38; коэффициент гамма γ=0,38.
Таблица 18
Критические значения коэффициента ранговой корреляции Спирмена
N |
Уровни значимости |
||
Р≤ 0,10 |
Р≤ 0,05 |
Р ≤ 0,01 |
|
4 |
1,000 |
1,000 |
|
5 |
0,800 |
0,900 |
1,000 |
6 |
0,657 |
0,829 |
0,943 |
7 |
0,571 |
0,714 |
0,893 |
8 |
0,524 |
0,643 |
0,833 |
9 |
0,483 |
0,600 |
0,783 |
10 |
0,455 |
0,564 |
0,745 |
11 |
0,427 |
0,536 |
0,709 |
12 |
0,406 |
0,503 |
0,671 |
13 |
0,385 |
0,484 |
0,648 |
14 |
0,367 |
0,464 |
0,622 |
15 |
0,354 |
0,443 |
0,604 |
16 |
0,341 |
0,429 |
0,582 |
17 |
0,328 |
0,414 |
0,566 |
18 |
0,317 |
0,401 |
0,550 |
19 |
0,309 |
0,391 |
0,535 |
20 |
0,299 |
0,380 |
0,520 |
21 |
0,292 |
0,370 |
0,508 |
22 |
0,284 |
0,361 |
0,496 |
23 |
0,278 |
0,353 |
0,486 |
24 |
0,271 |
0,344 |
0,475 |
25 |
0,265 |
0,337 |
0,466 |
26 |
0,259 |
0,331 |
0,457 |
27 |
0,255 |
0,324 |
0,448 |
28 |
0,250 |
0,317 |
0,440 |
29 |
0,245 |
0,312 |
0,433 |
30 |
0,240 |
0,306 |
0,425 |
31 |
0,236 |
0,301 |
0,418 |
32 |
0,232 |
0,296 |
0,412 |
33 |
0,229 |
0,291 |
0,405 |
34 |
0,225 |
0,287 |
0,399 |
35 |
0,222 |
0,283 |
0,394 |
36 |
0,219 |
0,279 |
0,388 |
37 |
0,216 |
0,275 |
0,383 |
38 |
0,212 |
0,271 |
0,378 |
39 |
0,210 |
0,267 |
0,373 |
40 |
0,207 |
0,264 |
0,368 |
41 |
0,204 |
0,261 |
0,364 |
Коэффицицент тау Кендала (t) определяется при наличии среди оцениваемых переменных порядковых переменных (или качественных признаков). При наличии среди переменных повторяющихся значений оценку зависимости целесообразно проводить на основе коэффициента гамма (γ).
Задания для самостоятельной работы
Задание 1. По данным задания проверьте гипотезу о равенстве нулю коэффициента корреляции между переменными: Х1и Х2. Изучали зависимости между живой массой (кг) – выборка 1 и содержанием гемоглобина (Hb % по Сали) – выборка 2 у павианов гамадрилов.
Выборка 1: 17 18 18 19 19 20 21 22 23 25
Выборка 2. 70 74 78 72 77 76 88 80 77
Задание 2. По данным задания проверьте гипотезу о равенстве нулю коэффициента корреляции между парными переменными Х3 и Х4.
Х3: 70 71 72 74 75 70 80 75 80
Х4: 4,0 4,5 3,5 5,5 5,3 6,0 7,4 7,5 7,5