3. Графическая интерпретация эмпирических зависимостей

Частотные распределения изображаются также в виде диаграмм и графиков. Главным достоинством графического изображения яв­ляется его наглядность.

Графическая интерпретация эмпирических зависимостей осно­вана на знании технических правил построения рядов, типов и свойств теоретических распределений. Здесь мы рассмотрим графики вариационных рядов: гистограмму, полигон и кумуляту распреде­ления.

Гистограмма. Гистограмма — это графическое изображений ин­тервального ряда. По оси абсцисс откладывают границы интервалов, на которых строят прямоугольники с высотой, пропорциональной плотностям распределения соответствующих интервалов (пропорциональной числу единиц совокупности, приходящейся па единицу длины интервала). При равных интервалах плотности распределения

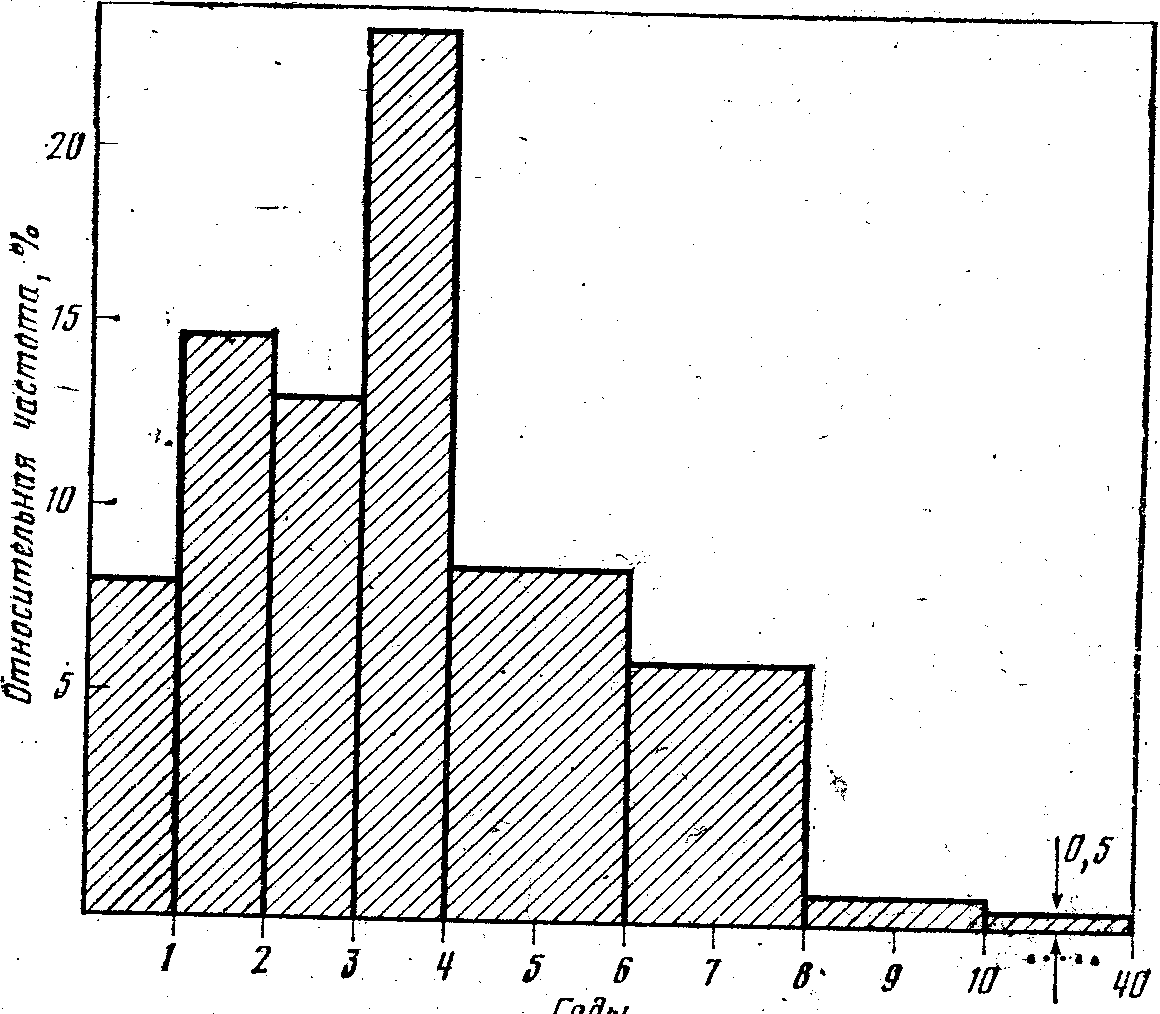
Рис. 1. Гистограмма распределения соотношения брачных возрастов разводя­щихся супругов

пропорциональны частотам, которые и откладываются по оси ординат (рис. 1, табл. 2).

Таблица 2. Распределение брачных возрастов разводящихся супругов.

Показатели	Муж старше жены (на сколько лет)
	меньше года	1-2	2-3	3-4	4-6	6-8	8-10	10 и более
Число людей	6	12	11	19	14	7	1	13
% к общему числу	7,2	14,5	13,2	22,9	16,9	8,4	1,2	15,7
Накопленная частота	6	18	29	48	62	69	70	83
Накопленная относительная частота, %	7,2	21,7	34,9	57,8	74,7	83,1	84,3	100

На гистограмме общее число лиц в каждой категории выражает­ся площадью соответствующего прямоугольника, а общая площадь равна численности совокупности (так как гистограмма на рис. 1 строится по относительным частотам, то площадь равна единице (100%)). Поэтому для интервалов 4—6, 6—8, 8—10 в табл. 2, которые в 2 раза больше предыдущих, нужно брать высоты прямо­угольников в 2 раза меньшие. При нанесении на графике последне­го открытого интервала 10 лет и более условно будем считать верхней его границей 40 лет. Тогда ширина интервала равна 30 го­дам, а плотность распределения — около 0,5% (15,7 : 30 0,5).

Полигон распределения. Для построения полигона величина при­знака откладывается на оси абсцисс, а частоты или относительные частоты — на оси ординат. Из точек, соответствующих значениям признака, восстанавливаются перпендикуляры, равные по высоте частотам. Вершины перпендикуляров соединяются прямыми ли­ниями.

Для интервального ряда ординаты, пропорциональные частоте (или относительной частоте) интервала, восстанавливаются перпен­дикулярно оси абсцисс в точке, соответствующей середине данного интервала.

Следующие данные распределения рабочих в возрасте до 24 лет по тарифным разрядам (высококвалифицированные рабочие сельхозмашиностроения)⁸³ дают возможность построить полигон распределе­ния (рис. 2):

Разряд	I	II	III	IV	V	VI
Численность, % к итогу	8,4	22,6	31,9	24,1	6,2	0,3
Накопленные частоты	8,4	31,0	62,3	87,0	93,2	93,5

Условно принято крайние ординаты признака соединять с сере­динами примыкающих интервалов (на рис.. 2 эти замыкающие линии нанесены пунктиром). Однако для распределения, где концентрация событий увеличивается на концах полигона, такое изображение мо­жет привести к ложным представлениям о существе явления.

Кумулята. Для графического изображения вариационных рядов используются также кумулятивные кривые. При построении кумуляты, как и гистограммы, на оси абсцисс откладываются границы интервалов (либо значения дискретного признака), а на оси орди­нат — накопленные частоты {либо относительные частоты), соответ­ствующие верхним границам интервалов. Таким образом, отличие кумуляты от гистограммы в том, что на графике кумуляты столби­ки, пропорциональные частотам, последовательно накладываются: один на другой, так что высота последнего столбика является сум­мой высот столбиков гистограммы.

Кумулята округляет индивидуальные значения признака .в пре­делах интервала и представляет собой возрастающую ломаную линию.

Кумулята позволяет быстро определить процент лиц, находя­щихся ниже или выше заданной величины признака. Например, по данным табл. 3, процент семейств, в которых муж старше супруги не более, чем на 5 лет, равен 65 (рис. 3, точка А).

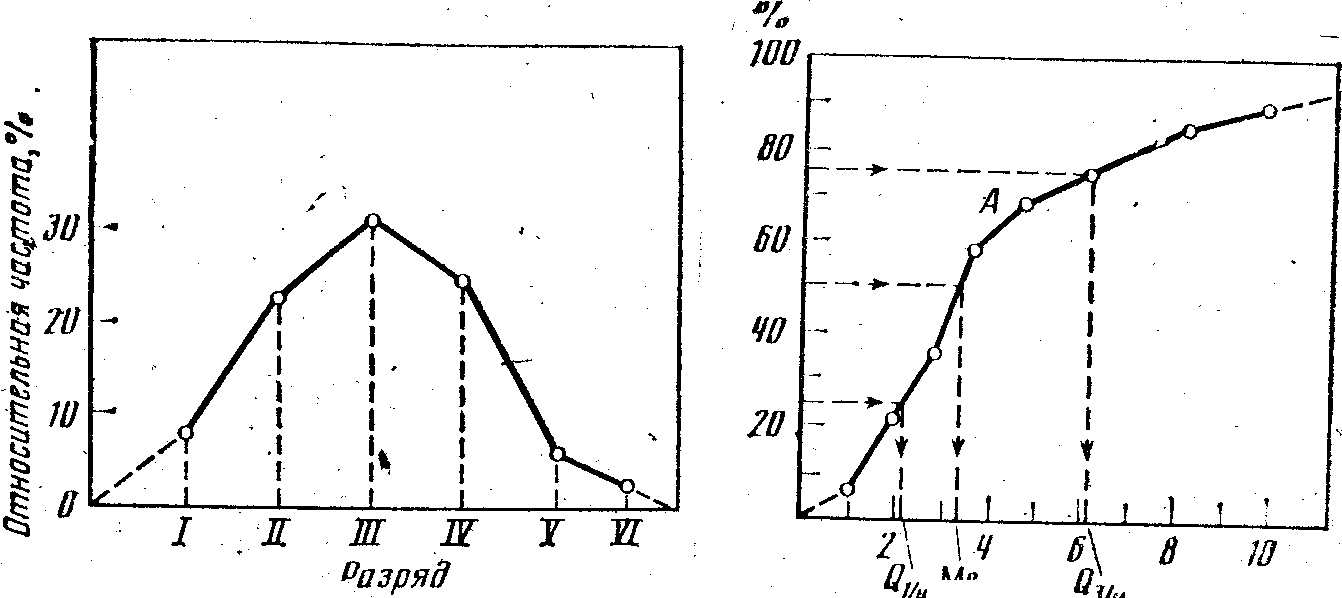
Число лет

Рис. 2. Полигон распределения работающих по тарифным разрядам

Рис. 3. Кумулята распределения соотношения брачных возрастов разводящих­ся супругов

Вид (форма) кривых распределений. Кривые, полученные в результате графического представления эмпирических данных, могут иметь разнообразную форму. Среди них можно выделить относи­тельно небольшое количество простых типов. Некоторые возможные формы распределений приведены на рис. 4. Анализ формы кривых иногда помогает в выявлении внутренней, скрытой структуры ис­следуемой совокупности. Например, можно предположить, что фор­ма кривой в обусловлена наложением двух кривых: а и б, иначе говоря, предположить, что существует третья скрытая переменная (или группа переменных), детерминирующая расчленение совокуп­ности на две группы.

Существует множество конкретных примеров того, как графический анализ стимулирует дальнейшее развитие исследовательской мысли.

Теоретическое распределение. Сбор эмпирической информации может быть осуществлен двумя путями: исследованием всей сово­купности социальных объектов, которые являются предметом изу­чения в пределах, очерченных программой социологического иссле­дования, и изучением лишь части этих объектов. В первом случае исследование называется сплошным, а множество социальных объектов — генеральной совокупностью, во втором исследование на­зывается выборочным, а выделенная часть объектов — выборкой⁸⁴.

Одна из основных задач статистики состоит в том, чтобы по данным выборки оценить параметры генеральной совокупности.

Гистограмма и полигон распределения, построенные на основ эмпирических данных выборки, позволяют выявить лишь приближенную картину реального распределения в генеральной совокуп­ности.

Рис. 4. Различные формы кривых распределения

Рис. 5. Теоретическая кривая распределения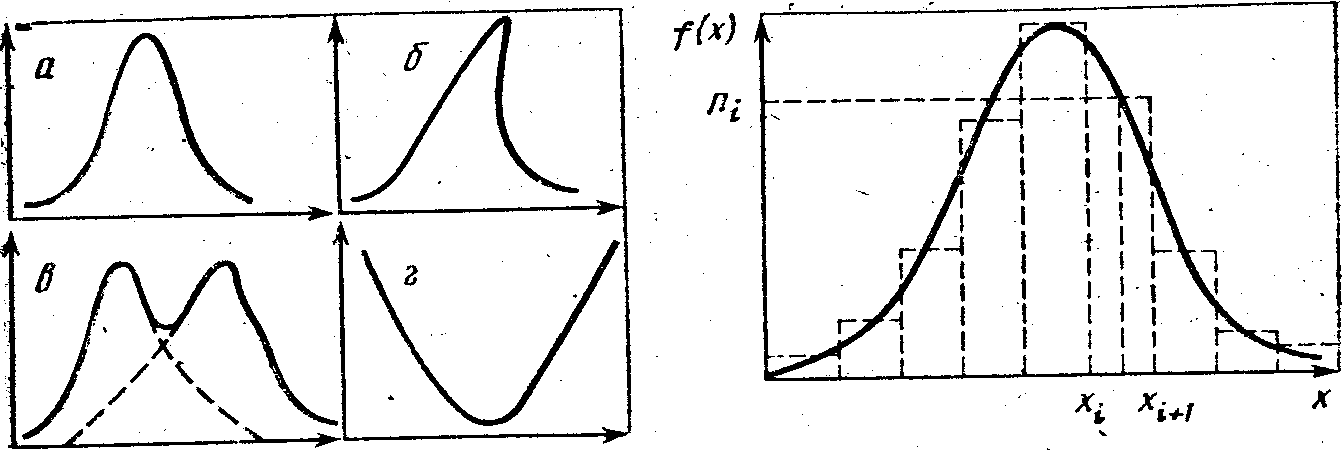

При увеличении выборочной совокупности и все большем дроб­лении величины интервалов эмпирическое распределение в вида гистограммы или полигона все более приближается к некоторой кривой, называемой кривой распределения.

Если группировочный признак является непрерывной величиной, то в предельном случае при постепенном уменьшении величин и интервала полигону и гистограмме будет соответствовать некоторая Гладкая кривая (рис. 5). Эта кривая распределения, являющаяся предельным случаем полигона данного эмпирического распределения, называется по установившейся, терминологии кривой плотности распределения. Обозначим .соответствующую функцию f(x).

В терминах теории вероятностей плотность распределения можно трактовать следующим образом: вероятность (p) того, что слу­чайная величина () примет значение из достаточно малого интер­вала (x_ix_i+1), равна произведению длины интервала на высоту пря­моугольника (f(x_i)), т. е.

Для интервала произвольной длины суммированием этих значе­ний получим, что

Отсюда приходим к определению фундаментального понятия теории вероятностей — функции распределения (F) случайной ве­личины (), которая по определению есть

Знание функции распределения дает исчерпывающее представление о поведении совокупности в отношении изучаемого признака, поэто­му определение типа распределения признаков представляет одну из задач исследования массовых явлений/