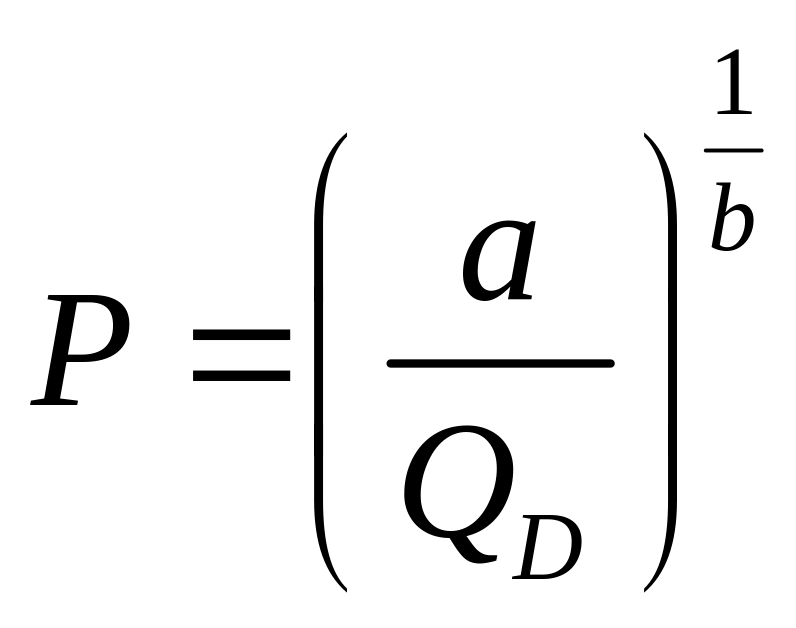- •Частина V. Алгоритми розв’язання задач в іспез з дисципліни «Мікроекономіка» для студентів економічних спеціальностей
- •Тема I. «теорія корисності»
- •I.2.1. Економічна інтерпретація:
- •I.2.2. Математична інтерпретація:
- •Тема V. «еластичність попиту і пропозиції»
- •Тема VI. «типи ринкових структур» Ринок досконалої конкуренції
- •Монопольний ринок
- •Олігополія і монополістична конкуренція
- •Ринок монополістичної конкуренції
- •Тема VII. «ринки факторів виробництва» Ринок праці
- •Ринок капіталу
- •Тема viіi. «загальна ринкова рівновага»
Частина V. Алгоритми розв’язання задач в іспез з дисципліни «Мікроекономіка» для студентів економічних спеціальностей
Тема I. «теорія корисності»
I.1.1. Економічна інтерпретація:
Знаходження
граничної корисності споживача
![]() від товару
від товару
![]() на основі функції його загальної
корисності
на основі функції його загальної
корисності
![]() .
.
I.1.2. Математична інтерпретація:
Знаходження похідної функції з однією змінною.
![]() .
.
Приклади.
Функція загальної корисності |
Функція граничної корисності |
|
|
|
|
|
|
|
|
|
|
![]() ,
,
![]() - дійсні числа, константи.
- дійсні числа, константи.
I.2.1. Економічна інтерпретація:
Знаходження
граничних корисностей для споживача
![]() ,
,
![]() від товарів
та
від товарів
та
![]() відповідно на основі функції його
загальної корисності
відповідно на основі функції його
загальної корисності
![]() .
.
I.2.2. Математична інтерпретація:
Знаходження часткових похідних функції з двома змінними.
![]() .
.
Приклади.
Функція загальної корисності |
Функція граничної корисності |
|
|
|
якщо
якщо
якщо
|
|
|
|
, |
|
|
|
|
|
, . |
![]() ,
,
,
,
![]() ,
,
,
,
![]() - дійсні числа, константи.
- дійсні числа, константи.
I.3.1. Економічна інтерпретація:
Знаходження загальної корисності споживача від товару на основі функції його граничної корисності .
I.3.2. Математична інтерпретація:
Знаходження невизначеного інтегралу функції з однією змінною.
![]() .
.
Приклади.
Функція граничної корисності |
Функція загальної корисності |
|
|
|
|
|
|
![]() ,
,
,
,
,
,
![]() - дійсні числа, константи.
- дійсні числа, константи.
I.4.1. Економічна інтерпретація:
Знаходження
обсягу споживання
![]() ,
при якому гранична корисність – нульова
,
при якому гранична корисність – нульова
![]() і досягається максимальна загальна
корисність
і досягається максимальна загальна
корисність
![]() .
.
I.4.2. Математична інтерпретація:
Знаходження максимуму функції з однією змінною.
![]() .
.
I.5.1. Економічна інтерпретація:
Знаходження
граничної норми заміщення
![]() товару
на товар
при заданій функції загальної корисності
від двох товарів -
та
.
товару
на товар
при заданій функції загальної корисності
від двох товарів -
та
.
I.5.2. Математична інтерпретація:
Знаходження часткових похідних функції і відношення двох функцій.
![]() .
.
I.6.1. Економічна інтерпретація:
Знаходження
граничної норми заміщення
товару
на товар
при заданій у явному вигляді функції
загальної корисності
![]() .
.
I.6.2. Математична інтерпретація:
Знаходження похідної функції з однією змінною.
![]() .
.
Приклади.
Функція загальної корисності |
Гранична норма заміщення |
|
|
|
|
|
|
|
|
![]() ,
,
,
,
,
,
![]() - дійсні числа, константи.
- дійсні числа, константи.
I.7.1. Економічна інтерпретація:
Знаходження
граничної корисності для дискретних
значень загальної корисності
![]() і
і
![]() й обсягів споживання
й обсягів споживання
![]() і
і
![]() .
.
I.7.2. Математична інтерпретація:
Знаходження
відношення приросту функції однієї
змінної
![]() до приросту аргументу
до приросту аргументу
![]() .
.
![]() .
.
I.8.1. Економічна інтерпретація:
Складання
рівняння бюджетного обмеження за даних
цін
![]() ,
,
![]() товарів
,
відповідно та рівня доходу споживача
товарів
,
відповідно та рівня доходу споживача
![]() .
.
I.8.2. Математична інтерпретація:
Складання загального рівняння прямої.
![]() .
.
I.9.1. Економічна інтерпретація:
Знаходження
рівноважного набору товарів
та
![]() ,
за якого максимізується загальна
корисність споживача
при даних цінах
,
і доході
споживача.
,
за якого максимізується загальна
корисність споживача
при даних цінах
,
і доході
споживача.
I.9.2. Математична інтерпретація:
Розв’язання системи двох рівнянь із двома невідомими - та .
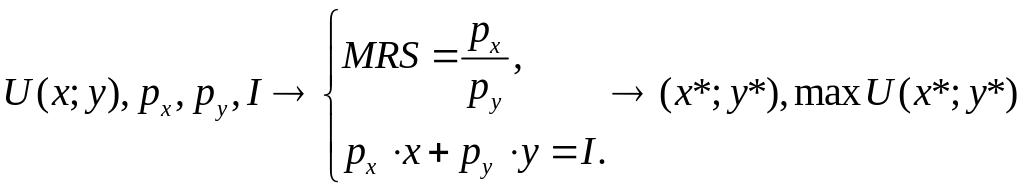 .
.
Тема ІІ. «ТЕОРІЯ ВИРОБНИЦТВА»
II.1.1. Економічна інтерпретація:
Знаходження
граничної продуктивності ресурсу
![]() на основі виробничої функції фірми
на основі виробничої функції фірми
![]() .
.
II.1.2. Математична інтерпретація:
Знаходження похідної функції з однією змінною.
![]() ,
,
Приклади.
Функція виробництва |
Функція граничної продуктивності |
|
|
|
|
|
|
|
|
|
|
,
,
![]() ,
- дійсні числа, константи.
,
- дійсні числа, константи.
II.2.1. Економічна інтерпретація:
Знаходження
граничних продуктивностей ресурсів
![]() ,
,
![]() факторів
факторів
![]() і
відповідно на основі виробничої функції
і
відповідно на основі виробничої функції![]() .
.
II.2.2. Математична інтерпретація:
Знаходження часткових похідних функції з двома змінними.
![]() .
.
Приклади.
Функція виробництва |
Функції граничних продуктивностей |
|
|
|
|
|
|
|
,
|
|
|
|
|
,
,
,
,
![]() - дійсні числа, константи.
- дійсні числа, константи.
II.3.1. Економічна інтерпретація:
Знаходження виробничої функції фірми на основі функції його граничної продуктивності .
II.3.2. Математична інтерпретація:
Знаходження невизначеного інтегралу функції з однією змінною.
![]() .
.
Приклади.
Функція граничної продуктивності |
Функція виробництва |
|
|
|
|
|
|
, , , - дійсні числа, константи.
II.4.1. Економічна інтерпретація:
Знаходження
обсягу ресурсу
,
при якому гранична продуктивність –
нульова (![]() )
і досягається максимальний обсяг випуску
продукції
)
і досягається максимальний обсяг випуску
продукції
![]() .
.
II.4.2. Математична інтерпретація:
Знаходження максимуму функції з однією змінною.
![]() .
.
II.5.1. Економічна інтерпретація:
Знаходження
граничної норми технологічного заміщення
![]() ресурсу
на ресурс
при заданій виробничій функції
від двох факторів виробництва -
і
.
ресурсу
на ресурс
при заданій виробничій функції
від двох факторів виробництва -
і
.
II.5.2. Математична інтерпретація:
Знаходження часткових похідних функції і відношення двох функцій..
![]() .
.
II.6.1. Економічна інтерпретація:
Знаходження
граничної норми технологічного заміщення
ресурсу
на ресурс
при заданій у явному вигляді виробничій
функції
![]() .
.
II.6.2. Математична інтерпретація:
Знаходження похідної функції з однією змінною.
![]() .
.
Приклади.
Функція загальної корисності |
Гранична норма заміщення |
|
|
|
|
, - дійсні числа, константи.
II.7.1. Економічна інтерпретація:
Знаходження
граничної продуктивності для дискретних
значень обсягів виробництва
![]() й
й
![]() та обсягів ресурсів
і
відповідно.
та обсягів ресурсів
і
відповідно.
II.7.2. Математична інтерпретація:
Знаходження відношення приросту функції до приросту аргументу.
![]() .
.
II.8.1. Економічна інтерпретація:
Складання
рівняння ізокости за даних цін ресурсів
![]() ,
факторів виробництва
,
відповідно і рівня загальних витрат
фірми
,
факторів виробництва
,
відповідно і рівня загальних витрат
фірми
![]() .
.
II.8.2. Математична інтерпретація:
Складання загального рівняння прямої.
![]() .
.
II.9.1. Економічна інтерпретація:
Знаходження
комбінації ресурсів
![]() і
і
![]() ,
за яких максимізується обсяг виробленої
продукції фірми
при даних цінах
,
і витратах фірми
.
,
за яких максимізується обсяг виробленої
продукції фірми
при даних цінах
,
і витратах фірми
.
II.9.2. Математична інтерпретація:
Розв’язання системи двох рівнянь із двома невідомими.
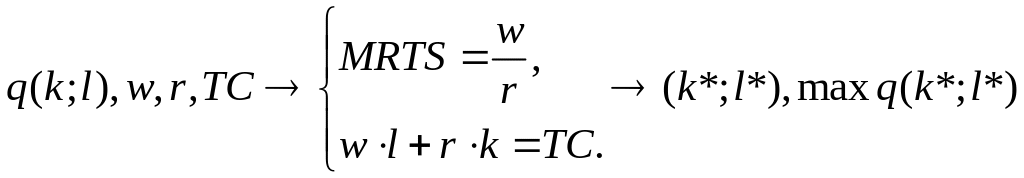 .
.
II.10.1. Економічна інтерпретація:
Знаходження
комбінації ресурсів
та
,
при яких мінімізуються витрати виробництва
для заданого обсягу продукції
![]() за фіксованих цін ресурсів
,
.
за фіксованих цін ресурсів
,
.
II.10.2. Математична інтерпретація:
Розв’язання системи двох рівнянь із двома невідомими.
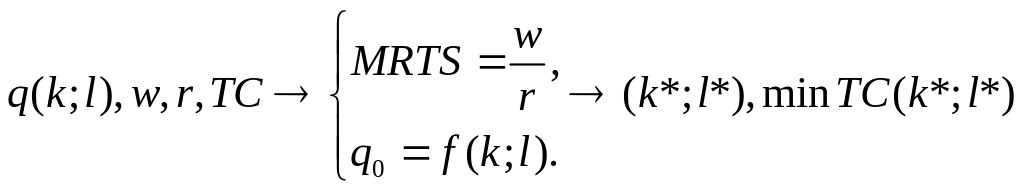 .
.
II.11.1. Економічна інтерпретація:
Знаходження
середньої продуктивності ресурсу
![]() на основі виробничої функції фірми
.
на основі виробничої функції фірми
.
II.11.2. Математична інтерпретація:
Знаходження відношення функції до аргументу.
![]() .
.
II.12.1. Економічна інтерпретація:
Знаходження
середніх продуктивностей ресурсів
![]() ,
,
![]() для факторів
і
відповідно на основі виробничої функції
.
для факторів
і
відповідно на основі виробничої функції
.
II.12.2. Математична інтерпретація:
Знаходження відношення функції до відповідних значень аргументів.
![]() .
.
II.13.1. Економічна інтерпретація:
Знаходження ефекту масштабу виробничої функції .
II.13.2. Математична інтерпретація:
Визначення однорідності чи неоднорідності функції з двома змінними.
(1) якщо
![]() ,
то функція має зростаючий ефект масштабу
(прогресивно-однорідна);
,
то функція має зростаючий ефект масштабу
(прогресивно-однорідна);
(2) якщо
![]() ,
то функція має спадний ефект масштабу
(дегресивно-однорідна);
,
то функція має спадний ефект масштабу
(дегресивно-однорідна);
(3) якщо
![]() ,
то функція має постійний ефект масштабу
(однорідна).
,
то функція має постійний ефект масштабу
(однорідна).
II.14.1. Економічна інтерпретація:
Знаходження максимальної середньої продуктивності для виробничої функції з одним фактором виробництва.
II.14.2. Математична інтерпретація:
Максимізація функції з однією змінною.
![]() або
або
![]() .
.
II.15.1. Економічна інтерпретація:
Знаходження максимальної середньої продуктивності для виробничої функції з двома факторами виробництва.
II.15.2. Математична інтерпретація:
Знаходження розв’язку рівняння з однією змінною.
![]() або
або
![]() .
.
Тема ІІІ. «ТЕОРІЯ ВИТРАТ»
III.1.1. Економічна інтерпретація:
Знаходження
похідного попиту на ресурс
![]() на основі однофакторної виробничої
функції фірми
.
на основі однофакторної виробничої
функції фірми
.
III.1.2. Математична інтерпретація:
Знаходження оберненої функції до заданої.
![]() .
.
Приклад.
-
Виробнича функція
Загальні витрати
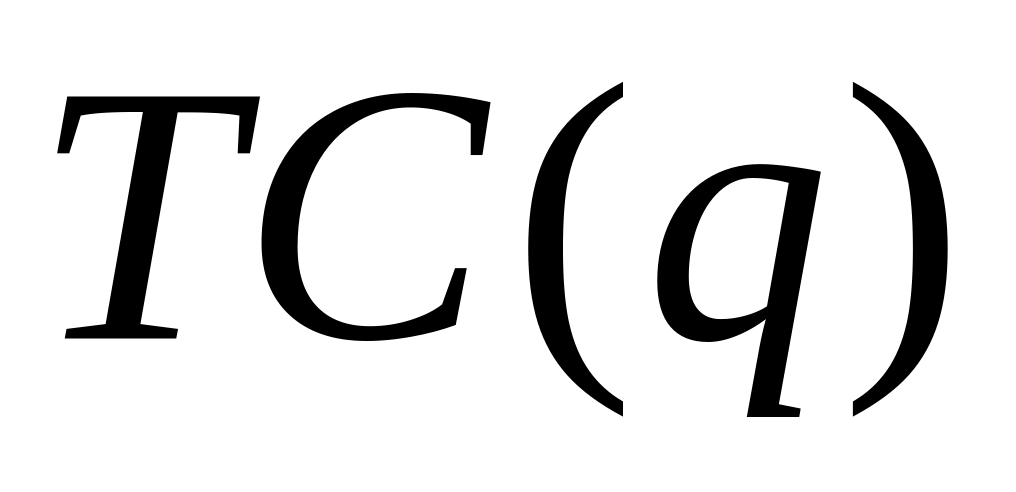

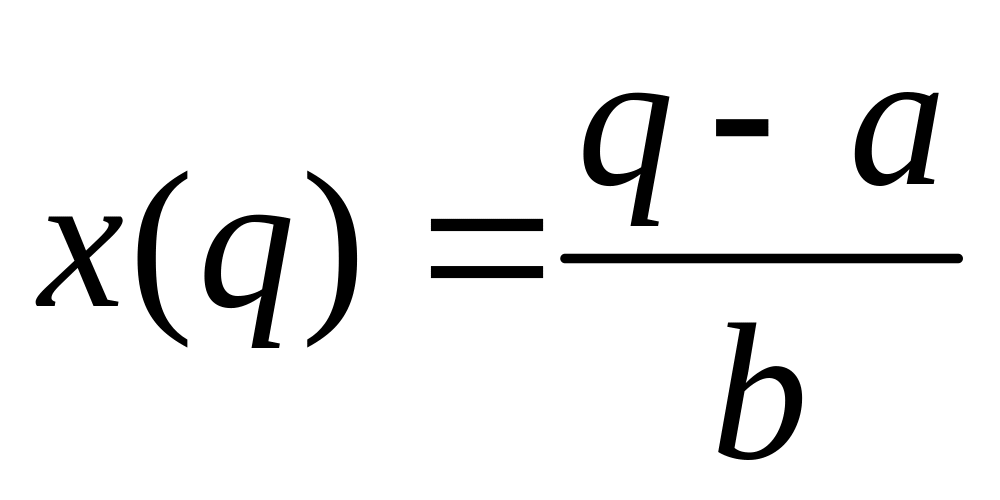
III.2.1. Економічна інтерпретація:
Знаходження
похідного попиту на ресурс
![]() ,
,
![]() на основі двофакторної виробничої
функції фірми
.
на основі двофакторної виробничої
функції фірми
.
III.2.2. Математична інтерпретація:
Знаходження обернених функцій до заданої.
![]() .
.
Приклади.
-
Виробнича функція
Загальні витрати
 ,
,
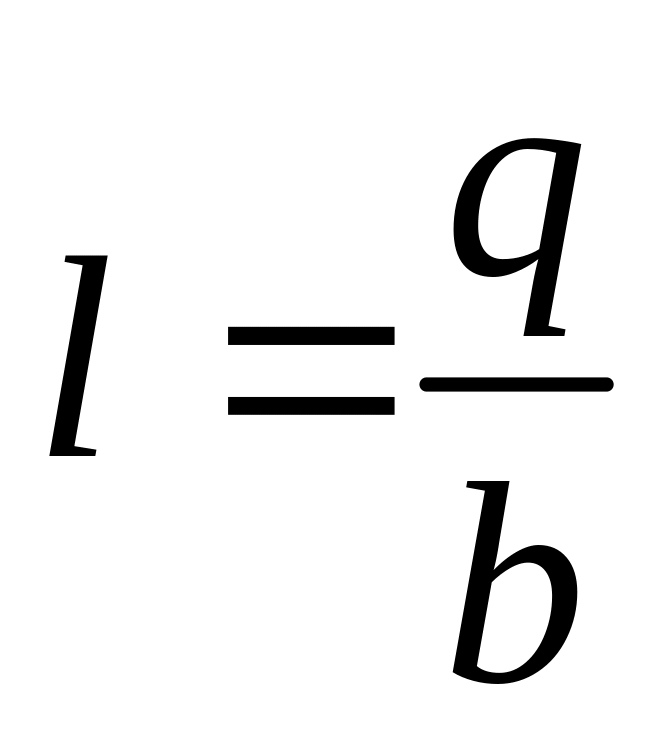
якщо
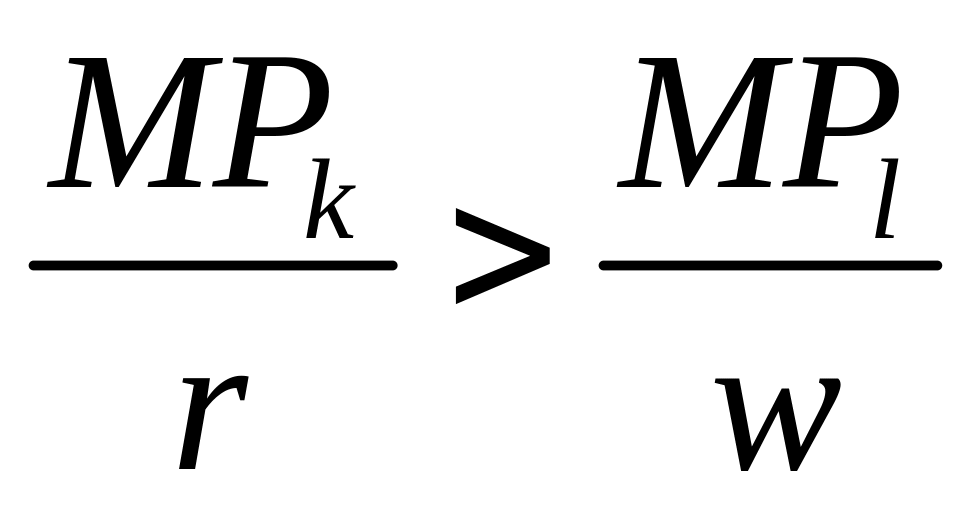 ,
то
,
то
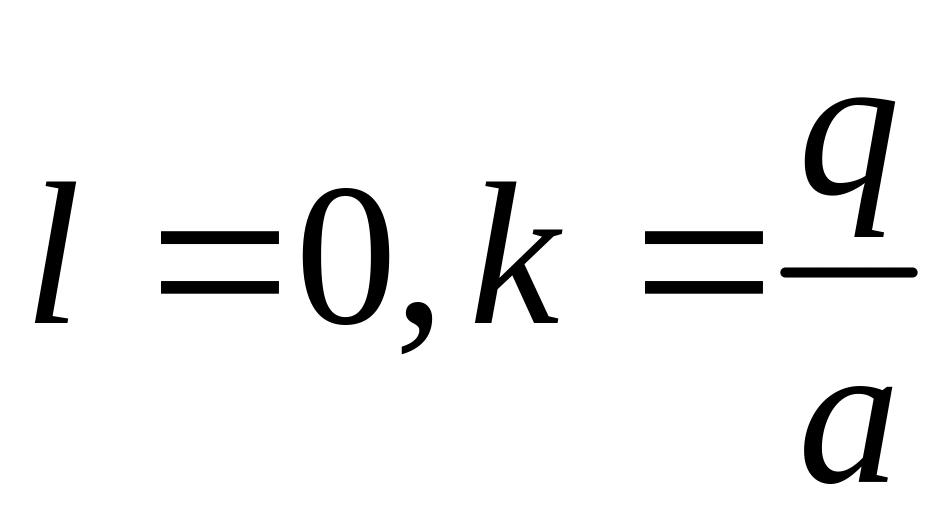 ;
;якщо
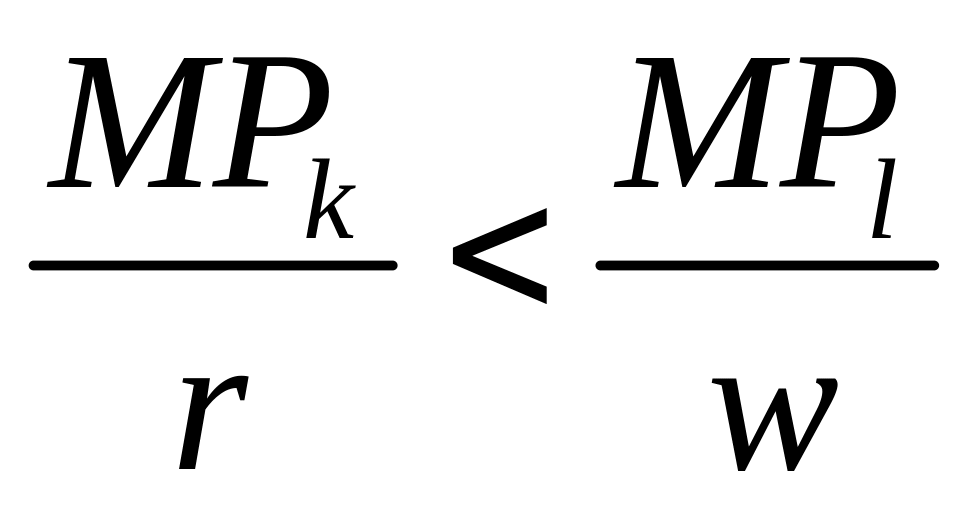 ,
то
,
то
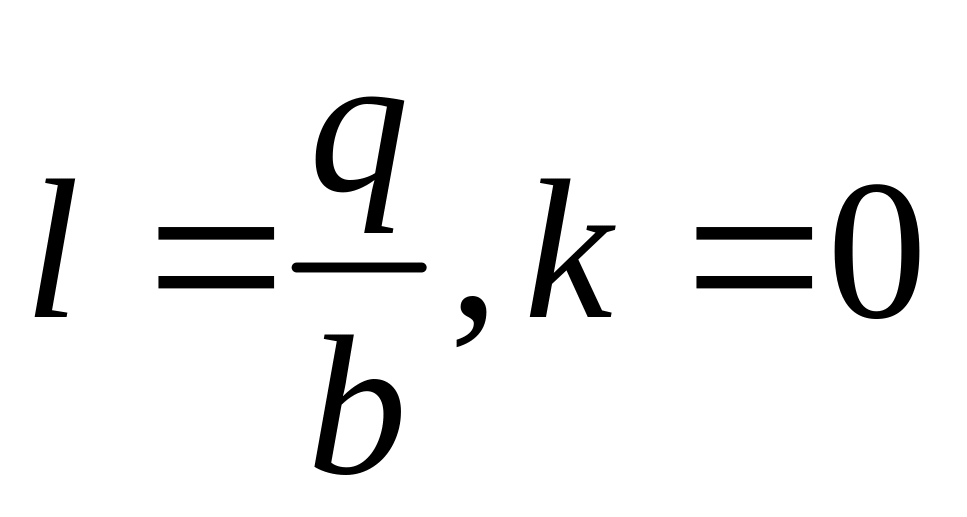 ;
;якщо
 ,
то
,
то
 ,
,
 .
.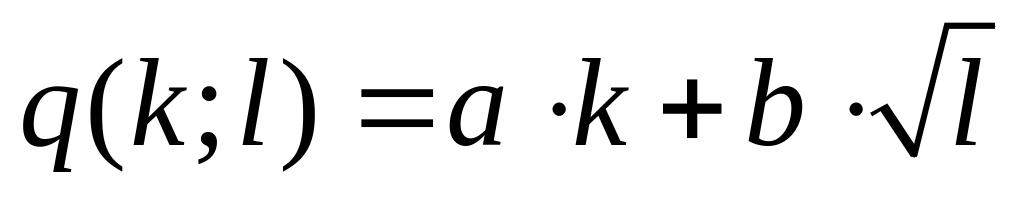
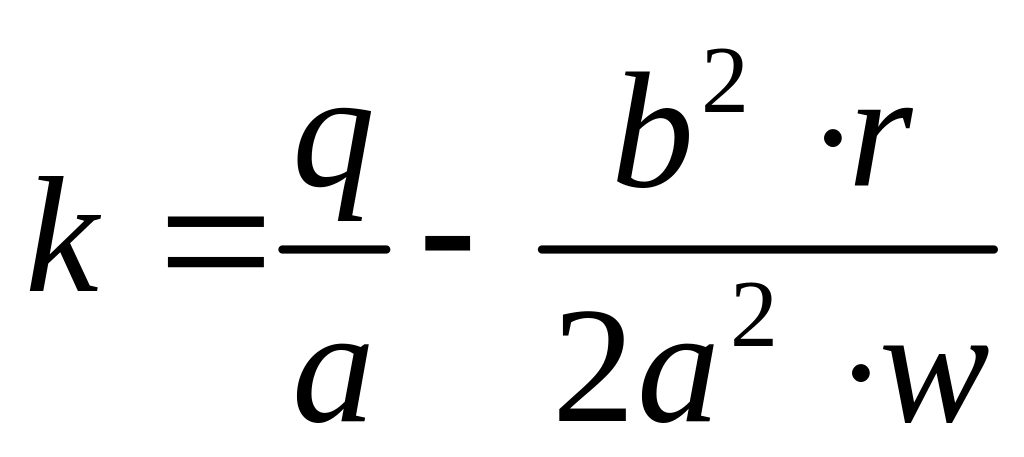 ,
,
 .
.
III.3.1. Економічна інтерпретація:
Знаходження загальних витрат на основі однофакторної виробничої функції фірми .
III.3.2. Математична інтерпретація:
Знаходження оберненої функції до заданої.
![]() .
.
Приклад.
-
Виробнича функція
Загальні витрати
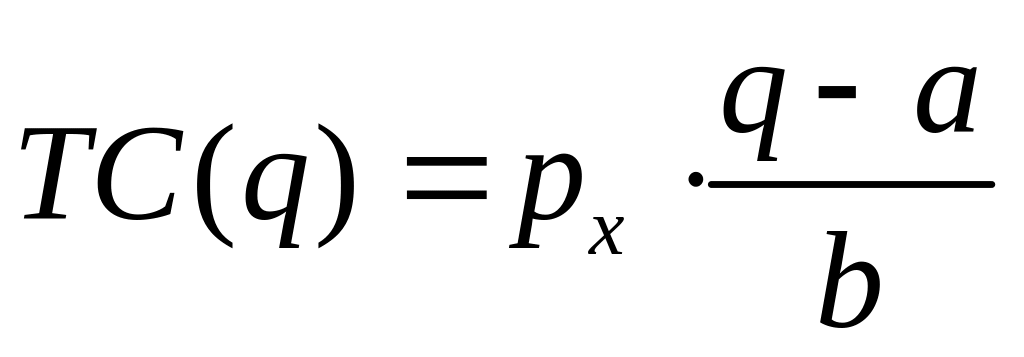
III.4.1. Економічна інтерпретація:
Знаходження загальних витрат на основі двофакторної виробничої функції фірми .
III.4.2. Математична інтерпретація:
Знаходження обернених функцій до заданої.
![]() .
.
Приклади.
-
Виробнича функція
Загальні витрати

якщо , то
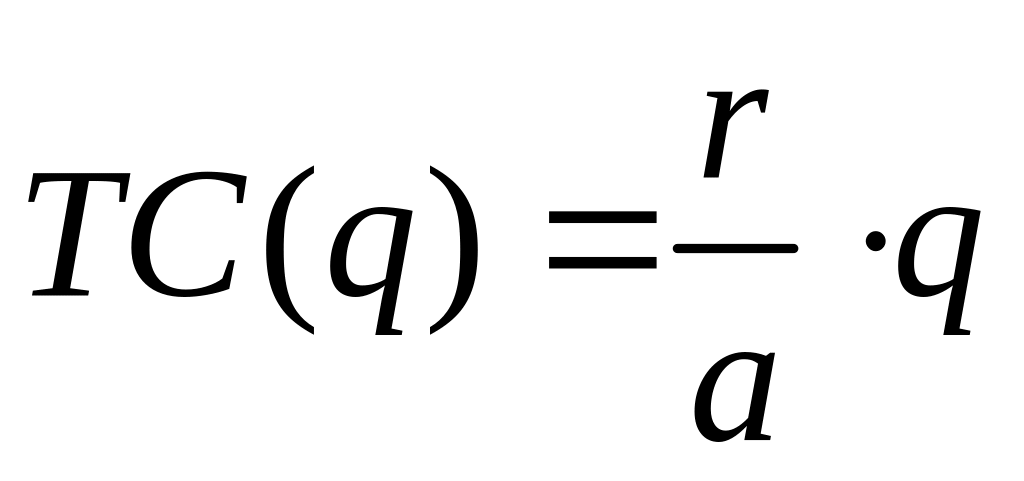 ;
;якщо , то
 ;
;якщо , то
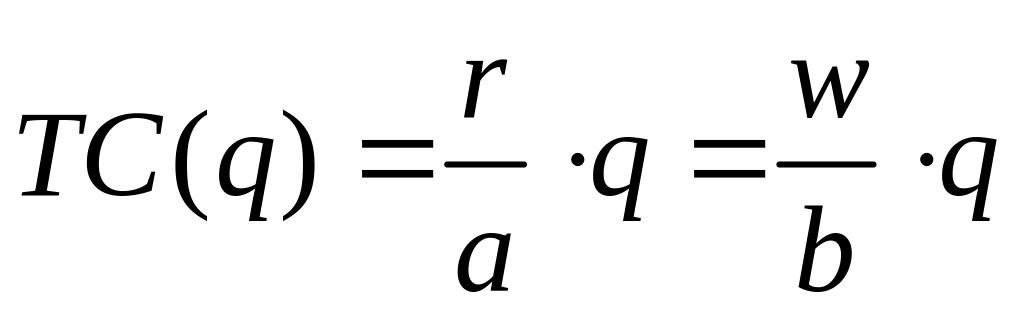 .
.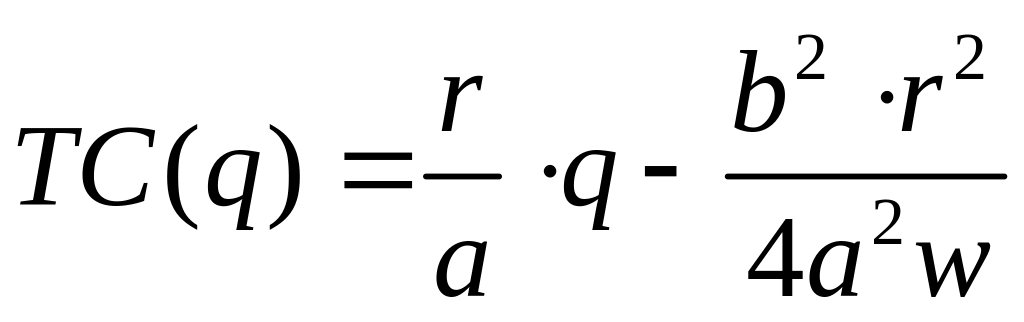
III.5.1. Економічна інтерпретація:
Знаходження
точкової еластичності загальних витрат
![]() на основі функції загальних витрат
.
на основі функції загальних витрат
.
III.5.2. Математична інтерпретація:
Знаходження добутку похідної функції і відношення виразів.
![]() .
.
III.6.1. Економічна інтерпретація:
Знаходження
постійних
![]() ,
змінних
,
змінних
![]() ,
середніх постійних
,
середніх постійних
![]() ,
середніх змінних
,
середніх змінних
![]() ,
середніх загальних
,
середніх загальних
![]() і граничних витрат
і граничних витрат
![]() на основі функції загальних витрат
.
на основі функції загальних витрат
.
III.6.2. Математична інтерпретація:
Знаходження абсолютних і відносних значень функції.
![]() ,
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Приклади.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
III.7.1. Економічна інтерпретація:
Знаходження
індивідуальної пропозиції фірми
![]() на основі функції загальних витрат
.
на основі функції загальних витрат
.
III.7.2. Математична інтерпретація:
Знаходження похідної функції з однією змінною.
![]() .
.
III.8.1. Економічна інтерпретація:
Знаходження обсягу випуску , за якого досягається мінімум функції середніх витрат виробництва .
III.8.2. Математична інтерпретація:
Знаходження мінімуму функції однієї змінної.
![]() або
або
![]() .
.
Тема ІV. «РИНКОВИЙ ПОПИТ І ПРОПОЗИЦІЯ»
ІV.1.1. Економічна інтерпретація:
Знаходження
рівноважної ціни
![]() та обсягу продажу
та обсягу продажу
![]() на конкурентному ринку за допомогою
функцій попиту
на конкурентному ринку за допомогою
функцій попиту
![]() і пропозиції
і пропозиції
![]() .
.
ІV.1.2. Математична інтерпретація:
Розв’язання системи двох рівнянь із двома невідомими.
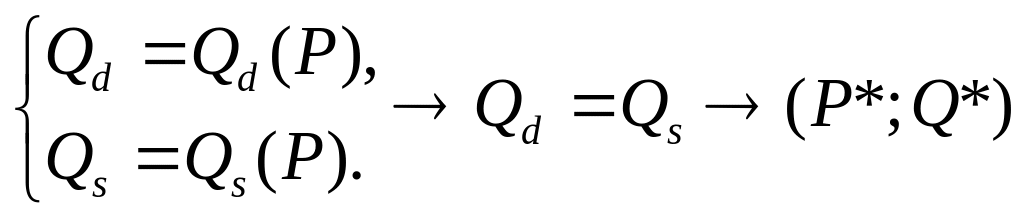 .
.
Приклад.
Функція попиту |
Функція пропозиції |
Рівноважна ціна |
Рівноважний обсяг |
|
|
|
|
ІV.2.1. Економічна інтерпретація:
Знаходження
нової рівноваги
![]() на конкурентному ринку під впливом
зміни нецінових факторів попиту і
пропозиції за допомогою заданих функцій
попиту
і пропозиції
.
на конкурентному ринку під впливом
зміни нецінових факторів попиту і
пропозиції за допомогою заданих функцій
попиту
і пропозиції
.
ІV.2.2. Математична інтерпретація:
Розв’язання системи двох рівнянь із двома невідомими.
![]() .
.
Приклади.
Функція попиту |
Функція пропозиції |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
,
,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() - нецінові фактори попиту і пропозиції.
- нецінові фактори попиту і пропозиції.
ІV.3.1. Економічна інтерпретація:
Знаходження
прямої функції ринкового попиту
![]() за допомогою прямих функцій індивідуального
попиту споживачів
за допомогою прямих функцій індивідуального
попиту споживачів
![]() за інших рівних умов (ціни інших товарів
за інших рівних умов (ціни інших товарів
![]() і дохід споживачів
і дохід споживачів
![]() є постійними).
є постійними).
ІV.3.2. Математична інтерпретація:
Знаходження
суми
![]() виразів.
виразів.

ІV.4.1. Економічна інтерпретація:
Знаходження
прямої функції ринкової пропозиції
![]() за допомогою прямих функцій індивідуальної
пропозиції фірм
за допомогою прямих функцій індивідуальної
пропозиції фірм
![]() за інших рівних умов (ціни ресурсів
праці
за інших рівних умов (ціни ресурсів
праці
![]() і капіталу
і капіталу
![]() є постійними).
є постійними).
ІV.4.2. Математична інтерпретація:
Знаходження суми виразів.
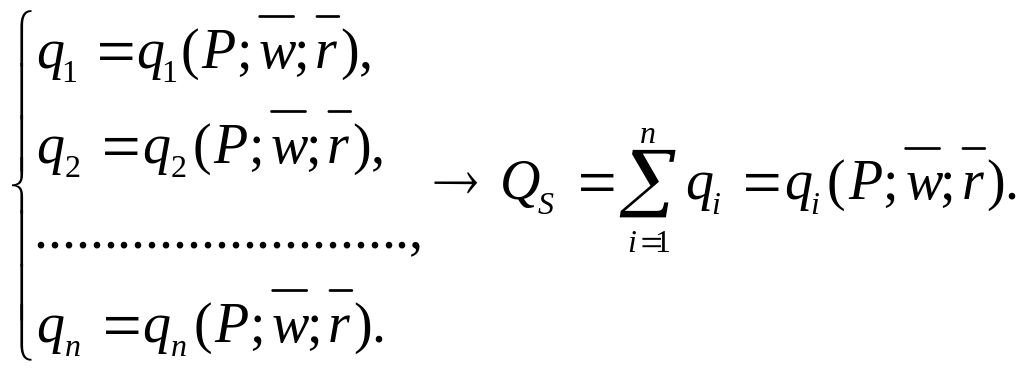
ІV.5.1. Економічна інтерпретація:
Обчислення
надлишку споживачів
![]() для конкурентного і монопольного ринків
за відомої функції ринкового попиту
для конкурентного і монопольного ринків
за відомої функції ринкового попиту
![]() при рівноважній ціні
й обсягу продаж
.
при рівноважній ціні
й обсягу продаж
.
ІV.5.2. Математична інтерпретація:
Розрахунок визначеного інтегралу для функції однієї змінної.
 .
.
ІV.6.1. Економічна інтерпретація:
Обчислення
надлишку виробників
![]() для конкурентного ринку за відомої
функції ринкової пропозиції
для конкурентного ринку за відомої
функції ринкової пропозиції
![]() при рівноважній ціні
й обсягу продаж
.
при рівноважній ціні
й обсягу продаж
.
ІV.6.2. Математична інтерпретація:
Розрахунок визначеного інтегралу для заданої функції однієї змінної.
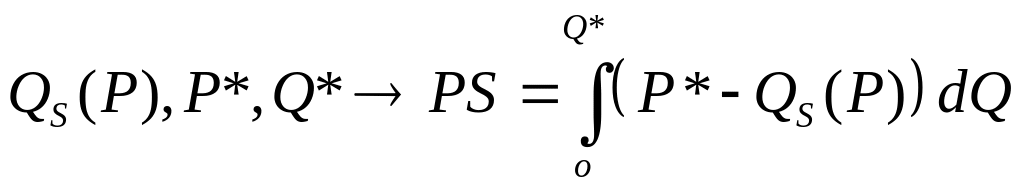 .
.
ІV.7.1. Економічна інтерпретація:
Визначення
суспільного добробуту
![]() для конкурентного ринку за відомих
функцій ринкового попиту
і ринкової пропозиції
.
для конкурентного ринку за відомих
функцій ринкового попиту
і ринкової пропозиції
.
ІV.7.2. Математична інтерпретація:
Розрахунок суми виразів або визначеного інтегралу для функції однієї змінної.
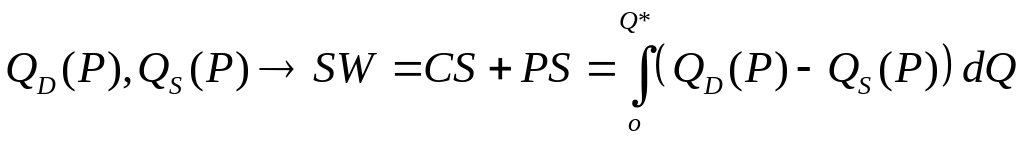 .
.
ІV.8.1. Економічна інтерпретація:
Обчислення оптимального обсягу випуску , за якого досягається максимальний суспільний добробут для конкурентного ринку за відомих функцій ринкового попиту і ринкової пропозиції .
ІV.8.2. Математична інтерпретація:
Знаходження першої і другої похідної функції з одним аргументом.
 .
.
ІV.9.1. Економічна інтерпретація:
Встановлення
оптимальної величини непрямого податку
![]() ,
за якого максимізується величина
надходжень до державного бюджету
,
за якого максимізується величина
надходжень до державного бюджету
![]() за відомих функцій ринкового попиту
і ринкової пропозиції
.
за відомих функцій ринкового попиту
і ринкової пропозиції
.
ІV.9.2. Математична інтерпретація:
Знаходження першої і другої похідної функції з одним аргументом.
![]() ,
,
де
![]() - обернена функція ринкового попиту,
- обернена функція ринкового попиту,
![]() - обернена функція ринкової пропозиції.
- обернена функція ринкової пропозиції.
Зауваження.
У залежності від того, встановлюється
державою податок чи субсидія, ціни
![]() і
і
![]() можуть знаходитись як на функції попиту,
так і пропозиції.
можуть знаходитись як на функції попиту,
так і пропозиції.
ІV.10.1. Економічна інтерпретація:
Обчислення
податкового тягаря для покупців
![]() і продавців
і продавців
![]() при встановленні непрямого податку
за відомих функцій ринкового попиту
і ринкової пропозиції
.
при встановленні непрямого податку
за відомих функцій ринкового попиту
і ринкової пропозиції
.
ІV.10.2. Математична інтерпретація:
Знаходження площі прямокутників.
![]() ,
,
де
- рівноважна ціна на конкурентному ринку
до встановлення непрямого податку,
![]() - рівноважний обсяг продаж після
встановлення податку.
- рівноважний обсяг продаж після
встановлення податку.
ІV.11.1. Економічна інтерпретація:
Визначення
розміру субсидії (дотації) для покупців
(продавців
)
при встановленні розміру субсидії
(дотації)
![]() за відомих функцій ринкового попиту
і ринкової пропозиції
.
за відомих функцій ринкового попиту
і ринкової пропозиції
.
ІV.11.2. Математична інтерпретація:
Знаходження добутку виразів.
![]() ,
,
де - рівноважна ціна на конкурентному ринку до встановлення субсидії (дотації), - рівноважний обсяг продаж після встановлення субсидії (дотації).
ІV.12.1. Економічна інтерпретація:
Знаходження
оберненої функції ринкового попиту
![]() за відомої прямої функції попиту
.
за відомої прямої функції попиту
.
ІV.12.2. Математична інтерпретація:
Знаходження оберненої функції.
![]() .
.
Приклади
Пряма функція попиту |
Обернена функція попиту |
|
|
|
|