Обходы графа в глубину и в ширину

Во многих задачах с использованием графов необходимо обходить все вершины и(или) ребра (дуги) графа. Обойти граф – это значит побывать во всех его вершинах по одному разу. Существует два классических алгоритма обхода графа – в глубину и в ширину.

Алгоритмы обхода дерева в глубину представляет обобщение алгоритма обхода дерева в прямом порядке.

Например, используя рекурсивную процедуру, алгоритм обхода графа G, заданного матрицей смежности, в глубину можно записать следующим образом:

procedure ОБХОД-В-ГЛУБИНУ(p:вершина);

begin

    Посетить вершину p;

    for all q from множества вершин, смежных с p do

        if q еще не посещалась then ОБХОД-В-ГЛУБИНУ(q) end

    end

end;

begin

    for all p from множества вершин G do

        if p еще не посещалась then ОБХОД-В-ГЛУБИНУ(p) end

    end

end.

Для того, чтобы отличать просмотренные вершины от непросмотренных можно ввести массив размерности n, чьи элементы будут принимать значения 1или 0 в зависимости от того просмотрена вершина или нет.

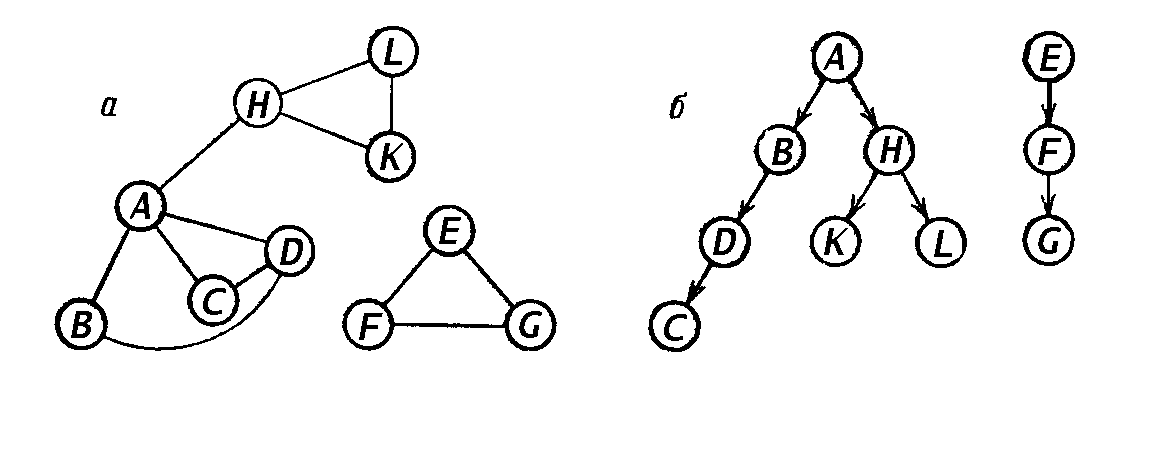
В результате работы алгоритма пройденные ребра графа образуют вместе с посещенными вершинами одно или несколько деревьев (по одному дереву для каждой компоненты связности графа). Если приписать пройденным ребрам ориентацию в соответствии с тем направлением, в каком они проходятся при выполнении алгоритма, то мы получим совокупность ордеревьев, причем их корнями будут служить все те вершины, которые в процессе работы алгоритма помещались в пустой стек. Например, для графа, изображенного на рис. а, описанным способом будут получены два ордерева, приведенных на рис. б. Порядок на всем множестве вершин графа, а также порядок вершин, смежных всякой его вершине, соответствует алфавитному порядку букв, помечающих вершины.

Нерекурсивный вариант алгоритма обхода графа G в глубину может иметь следующий вид:

procedure ОБХОД-В-ГЛУБИНУ-1(p: вершина);

begin

    Посетить вершину p и поместить ее в пустой стек S;

    while Стек S непуст do

            Пусть p -- вершина, находящаяся на верхушке стека S;

            if у p есть непосещенные смежные вершины then

                    Пусть q -- непосещенная вершина, смежная вершине p;

                    Пройти по ребру (p,q), посетить вершину q и поместить ее в стек S

            else Удалить вершину p из стека S

            end

    end

end;

Обход в ширину связного графа предполагает рассмотрение всех его вершин в порядке возрастания расстояния от некоторой вершины, с которой начался данный обход графа. То есть для вершины v сначала рассматриваются все вершины, смежные с ней и таким образом чем позже посмотрена вершина, тем позже она используются. Поэтому для хранения просмотренных вершин используется очередь. Например, в результате обхода графа G (рис. a) в ширину возможен следующий порядок посещения вершин: A, B, С, D, H, K, L, E, F, G  Следующий алгоритм позволяет осуществить обход в ширину любого связного графа G:

procedure ОБХОД-В-ШИРИНУ(p: вершина);

begin

    Поместить произвольную вершину p в пустую очередь O;

    while очередь O не пуста do

            Взять первую вершину p из очереди O;

            if p еще не посещалась then

                    Посетить вершину p и поместить в очередь O все непросмотренные вершины, смежные с p

            end

    end

end;