8. Многоугольники и их компоненты

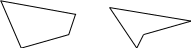Многоугольником или точнее n-угольником называют часть плоскости, ограниченную n-звенной (n  3) замкнутой ломаной без самопересечений. Вершины и звенья этой ломаной соответственно называют вершинами и сторонами этого многоугольника. На рисунке 12 (слева – направо) изображены выпуклый и невыпуклый четырехугольники. Под выпуклым многоугольником понимают такой, который расположен в одной полуплоскости относительно каждой прямой, проходящей через его стороны. Многоугольник является выпуклым тогда и только тогда, когда

все его внутренние углы меньше 180⁰.

Сумма всех внутренних углов любого

(и даже невыпуклого) n-угольника равна

(n – 2)180 ⁰. Отрезок, соединяющий не смеж-

ные (не лежащие на одной стороне) вершины Рис. 12

называется диагональю многоугольника. В n-угольнике n(n – 3)/2 диагоналей. Если d₁, d₂ – длины диагоналей четырехугольника, угол между которыми равен , то площадь этого четырехугольника может быть найдена по формуле . Оказывается, что в четырехугольнике, с перпендикулярными диагоналями, суммы квадратов противоположных сторон равны.

Окружность, проходящая через все вершины многоугольника, называют описанной около него, а окружность, касающуюся каждой его стороны, – вписанной в этот многоугольник. Ясно, что если около многоугольника описана окружность или в него вписана окружность, то он является обязательно выпуклым. Не во всякий даже выпуклый многоугольник можно вписать окружность, но если ее можно в него вписать, то она единственна и ее радиус может быть найден по формуле r = S/p, где S – площадь и p – полупериметр этого многоугольника. Также не около всякого многоугольника можно описать окружность. Если около некоторого многоугольника все же можно описать окружность, то она единственна и его обычно называют вписанным, а радиус этой окружности, зная информацию о двух каких-то смежных сторонах и углу между ними, можно найти как радиус окружности, описанной около треугольника, построенного на этих двух смежных сторонах многоугольника. Полезно знать связанные с описанной и вписанной окружностями четырехугольника следующие два утверждения:

- около четырехугольника можно описать окружность тогда и только тогда, когда сумма его двух каких-то противоположных углов равна 180⁰ ;

- в четырехугольник можно вписать окружность тогда и только тогда, когда он выпуклый и суммы его противоположных сторон равны.

Многоугольник, у которого все стороны равны и все внутренние углы тоже равны, называется правильным. В такой многоугольник можно вписать окружность, а также около него можно описать окружность, причем центры этих окружностей совпадают. Необходимые формулы, связанные с правильным n-угольником A₁A₂…A_n , можно получить в результате рассмотрения треугольника А₁ О А₂ , где О – центр вписанной (а значит и описанной) окружности. Действительно, угол А₁ О А₂ равен 360⁰ / n (кстати, внешний угол при вершине правильного n-угольника тоже равен 360⁰ / n), А₁ О – радиус описанной около многоугольника окружности, высота треугольника А₁ О А₂, проведенная из О, – радиус вписанной в многоугольник окружности, – площадь n-угольника и т. д.. Для примера приведем одну из версий таких формул для правильного n-угольника, в случае, когда известна длина а его стороны:

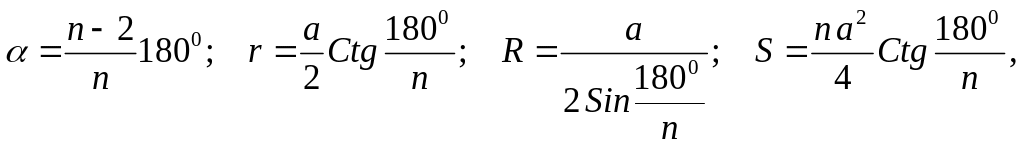
где , r, R и S - соответственно внутренний угол, радиус вписанной окружности, радиус описанной окружности и площадь этого правильного n-угольника.

Теперь можно переходить к решению заданий 3.1 – 3.5.

8.1. В пятиугольник с площадью 22 вписали окружность радиуса 2. Найдите наименьшую из его сторон, если их длины относятся как 3 : 2 : 1 : 2 : 3.

8.2. В правильном шестиугольнике А₁ А₂…А₆ проекция диагонали А₁ А₃ на диагональ А₃ А₆ равна . Найдите площадь вписанного в этот шестиугольник круга.

8.3. Около правильного многоугольника А₁ А₂ …А_n с внешним углом 30 ⁰ описана окружность радиуса . Найдите расстояние от точки А₁ до прямой А₃ А₈ .

8.4. Найдите диаметр окружности, описанной около четырехугольника со сторонами 7, 15, 20 и 24 .

8.5. В четырехугольник с перпендикулярными диагоналями вписана окружность. Найдите ее радиус, если известно, что какие-то две стороны четырехугольника равны 13 и 15 , а одна из его диагоналей равна 24 .