7. Окружности и подобные треугольники.

Говорят, что треугольник FGH подобен треугольнику АВС с коэффициентом k , когда  F =  A ,  G =  B,  H =  C, а также FG / AB = FH / AC = GH / BC = k. Если в ходе решения задания не важен коэффициент подобия k , то просто говорят, что треугольники FGH и АВС подобны и пишут  АВС   FGH . Необходимо знать три признака подобия треугольников: по двум пропорциональным соответствующим сторонам и равным углам между ними; по двум равным соответствующим углам; по трем пропорциональным соответствующим сторонам. Так же необходимо помнить, что коэффициент подобия треугольников может быть найден как отношение их соответствующих компонент, имеющих линейные размеры (например, как отношение соответствующих высот, медиан или биссектрис, а также как отношение периметров, радиусов вписанных или радиусов описанных окружностей и т. п.). Квадрат коэффициента подобия треугольников равен отношению площадей соответствующих фигур, связанных с этими треугольниками (например, отношению площадей самих треугольников, отношению площадей, вписанных в них кругов, и т.п.). Часто встречаются ситуации, когда подобные треугольники расположены как на рис. 6 при  ABC =  ADE или на рис. 7 при  GKL =  FGK . В этих ситуациях имеем  ABC   ADE и  HKL   HGF соответственно.

А F G

D H

E

B K L

Рис. 6 C Рис. 7

П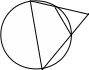 одобные треугольники встречаются и при решении заданий, связанных с окружностью. На рис. 8 – 11 приведены такие ситуации.

В A B

С F

F A D B (касательная) C

А B

F C

D Рис. 10 D

Рис. 8 C

D A

Рис. 9 Рис. 11

На каждом из рисунков 8 – 10 подобие треугольников AFD и CFB является необходимым и достаточным условием для того, чтобы точки A, B, C и D лежали на одной окружности.

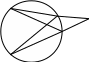
Из подобия этих треугольников следуют полезные соотношения: AFFC = BFFD на рисунке 8, CB : AD = FB : FD на рисунке 9, а если к тому же на этом рисунке угол DBF прямой, то есть FB : FD = Cos  ВFD, то получаем равенство СВ : АD = Cos  AFD. На рисунке 10 из подобия треугольников AFD и CFB следует, что FBFA = FDFC . На рисунке 11 подобными являются треугольники АВС и BDC (величины углов BAD и CBD равны половине угловой величины одной дуги BD , а угол С общий). Откуда получается полезное равенство для отрезка касательной ВС, имеющее вид ВС = .

Теперь можно переходить к решению заданий 2.1 – 2.5.

7.1. Стороны АВ и ВС треугольника АВС пересекает прямая, параллельная АС, соответственно в точках D и E . Периметр и площадь треугольника АВС равны 12 (ед. и ед.²).

Найдите радиус окружности, вписанной в треугольник BDE, если DA + AC + CE = 6+ DE.

7.2. Около треугольника АВС описана окружность. Продолжение медианы АD пересекает окружность в точке Е . Найдите длину отрезка СЕ, если AB = 8, AD = 12, AE = 15.

7.3. В треугольнике АВС точка D лежит на стороне АС, причем АD = 2, DС = 7 и  А = 45⁰. Найдите площадь треугольника АВD, если  АВD =  АСВ .

7.4. В треугольнике АВС проведены высоты ВD и СЕ. Найдите DЕ, если AB / AD = 3 и ВС = 15.

7.5. На стороне АС треугольника АВС как на диаметре построена окружность, пересекающая прямые АВ и ВС в двух точках D и E соответственно. Найдите сторону ВС, если известно, что АВ = 1 и АС = 2DE = .