Методичні вказівки

Вважаючи, що використовувані для розрахунку показники отримані на основі вибіркових даних, необхідно розрахувати граничну помилку вибірки за формулою:

і межі зміни середнього рівня показника в генеральній сукупності:

(розрахунки виконати за факторною ознакою).

Для відповіді на друге питання необхідно визначити за вибірковим даними кількість підприємств (робітників), що мають факторну ознаку вище за середнє значення , розраховане за вибірковим даними. Потім слід визначити частку

,

граничну помилку частки

й межі частки в генеральній сукупності

Для відповіді на третє питання необхідно визначити граничну помилку, що допускається за умовою завдання: , потім розрахувати обсяг вибірки за формулою:

Лабораторна робота №5 Тема: "Індекси"

Мета: Засвоїти правила побудови індивідуальних і загальних індексів, навчитися правильно застосовувати форму загального індексу, виходячи з наявних вихідних даних, грамотно інтерпретувати значення індексів, отриманих в результаті розрахунків.

Завдання:

1. Визначити індивідуальні й агрегатні індекси кількісних, якісних і об'ємних показників. Розрахувати загальний абсолютний приріст об'ємного показника, у т.ч. за рахунок впливу зміни кількісного і якісного показників. Зробити економічні висновки за виконаними розрахунками (використовувати дані додатків Б і В).

2. Обчислити відповідні середні з індивідуальних індексів, а також загальні індекси, що входять у систему їх взаємозв'язку. Зробити висновки (використовувати дані додатків Г і Д).

3. На основі розрахунку індексів середніх величин (змінного, постійного складу й структурних зрушень) оцінити динаміку середньої величини якісного показника. Визначити абсолютний приріст об'ємного показника - усього, і по факторах (використовувати дані додатку Є).

Методичні вказівки Індивідуальні індекси будуються при аналізі зміни простий простих явищ або окремих елементів складних економічних явищ:

, ,

Найважливішою формою загальних індексів є агрегатні індекси. При побудові агрегатних індексів якісних показників ваги в чисельнику й знаменнику формули фіксуються на рівні звітного періоду:

При цьому різниця між чисельником і знаменником має реальний економічний зміст, тобто показує розмір економії або перевитрати за рахунок зміни якісного показника:

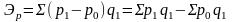
При побудові агрегатних індексів кількісних показників вагами служать якісні показники, які фіксуються в чисельнику й знаменнику формули на рівні базисного періоду:

Дотримання цієї умови дозволяє зберегти реально існуючий взаємозв'язок індексів:

Агрегатні індекси в оцінці зміни кількісних і якісних показників застосовуються за умови наявності інформації про значення цих показників у звітному й базисному періодах. У випадку, коли в умові завдання немає даних про абсолютні значення значеннях кількісних і якісних показників, а є відомості про їхню відносну зміну (індивідуальні індекси), прибігають до розрахунку загальних індексів, як середніх з індивідуальних індексів.

Для якісних показників середній індекс визначається як середній гармонійний:

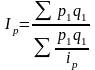
Для кількісних показників середній індекс визначається як середній арифметичний:

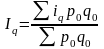
Для оцінки зміни середньої величини якісного показника застосовується система індексів: змінного, постійного складу і структурних зрушень.

Індекс змінного складу дорівнює співвідношенню середніх рівнів величин, які індексуються, звітного й базисного періодів. Якщо, наприклад, вивчається динаміка середньої собівартості однойменної продукції по декільком підприємствам, то індекс собівартості змінного складу обчислюється за формулою:

Зниження середньої собівартості може бути обумовлене зниженням собівартості цього виду продукції на окремих підприємствах і підвищенням питомої ваги виробництва продукції в загальному його обсязі підприємствами з більш низькою собівартістю.

Для виявлення впливу кожного фактора на зміну середньої собівартості слід обчислити індекс постійного (фіксованого) складу й індекс структурних зрушень. Індекс постійного складу характеризує зміну середньої собівартості за рахунок зміни тільки собівартості продукції й визначається за формулою:

Зміна середньої собівартості за рахунок фактора структурних зрушень у випуску продукції підприємствами оцінюється з за допомогою індексу структурних зрушень:

Зазначені три індекси зв'язані між собою:

На основі цієї індексної системи можна розкласти по факторах абсолютний приріст об'ємного показника, тобто, наприклад, витрат на випуск однойменної продукції:

Цей приріст обумовлений зміною:

а) кількості виробленої продукції:

б) у структурі обсягу виробництва продукції підприємствами:

в) собівартості виробництва продукції даного виду по окремих підприємствах: Таким чином, загальний приріст витрат можна представити, як приріст по факторах:

+ +