
- •1. Введение
- •2. Теоретическая часть: Методы решения стереометрических задач.
- •2.1 Поэтапно-вычислительный метод.
- •2.2 Координатный метод
- •Практическая часть.
- •3.1. Расстояние между двумя точками.
- •3.2. Расстояние от точки до прямой
- •3.3. Расстояние от точки до плоскости
- •3.4. Угол между двумя прямыми
- •4.Заключение.
- •5.Приложения
- •2. Правильная треугольная призма
- •3.Правильная шестиугольная призма
- •4. Правильная треугольная пирамида
- •5. Правильная четырехугольная пирамида
- •6. Правильная шестиугольная пирамида
4. Правильная треугольная пирамида
Правильная треугольная пирамида MABC , сторона основания которой равна a , а высота h .Обычно используют один из двух вариантов расположения системы координат.
4.1
Пусть начало координат находится в
точке A
,
ось x
направлена
вдоль ребра AC
,
ось y
проходит
через точку A
перпендикулярно
AC
,
ось z
проходит
через точку A
перпендикулярно
плоскости ABC
(см.
рис. 6). Тогда вершины пирамиды имеют
координаты: А(0; 0; 0); В(
;
;
0);С(а;0;0), М(
;
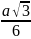 ;h).
;h).
4.2
Пусть начало координат находится в
центре треугольника ABC
в
точке O
,ось
x
проходит
через точку O
параллельно
ребру AC
,
ось y
проходит
через точку O
перпендикулярно
AC
,
ось z
проходит через точку O
перпендикулярно
плоскости ABC
(см.
рис. 7). Тогда вершины пирамиды имеют
координаты: A(-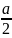 ;
-
;0),
В(0;
;
-
;0),
В(0;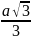 ;
0),
;
0),
С( ; - ;0), М(0;0;h).
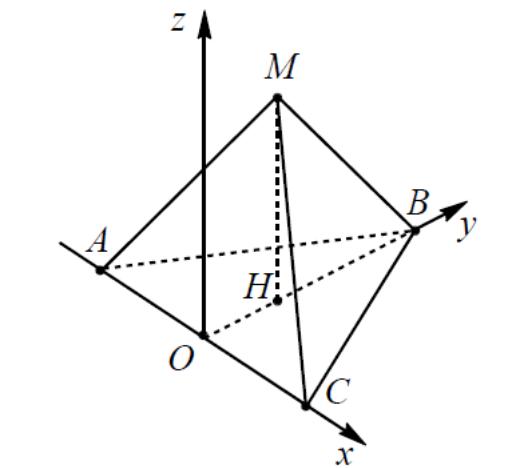
4.3 Еще один вариант расположения правильной треугольной пирамиды относительно прямоугольной декартовой системы координат представлен на рисунке №8.
5. Правильная четырехугольная пирамида
Правильная четырехугольная пирамида MABC , сторона основания которой равна a , а высота h .Обычно используют один из двух вариантов расположения системы координат.
5.1 Пусть начало координат находится в точке A , ось x направлена вдоль ребра AD , ось y – вдоль ребра AB , ось z
проходит через точку A перпендикулярно плоскости ABC (см. рис. 9). Тогда вершины пирамиды имеют координаты: A(0; 0; 0) , B(0; a; 0) , C(a; a; 0) ,Д(а;0;0), М( ; ; h).
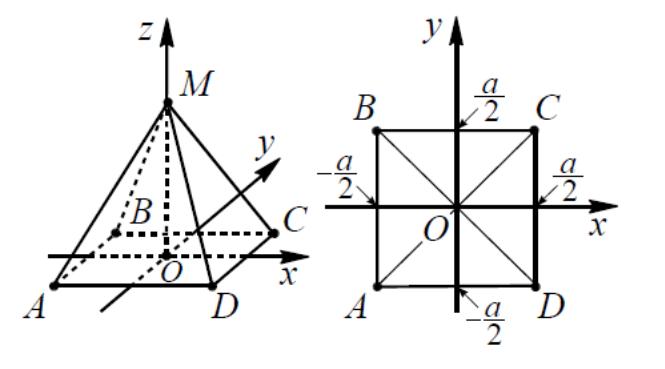
5.2. Пусть начало координат находится в центре основания в точке O , ось x проходит через точку O параллельно ребру AD , ось y проходит через точку O параллельно ребру AB, ось z проходит через точку O перпендикулярно плоскости основания (см. рис. 10). Тогда вершины пирамиды имеют координаты:
А(- ; - ;0), В (- ; ;0), С( ; ;0),Д( ; - ;0),М(0;0;h)
6. Правильная шестиугольная пирамида
6.1MABCDEF , сторона основания которой равна a , а высота h . Пусть начало координат находится в точке A , ось x направлена вдоль ребра AC , ось y проходит через точку A перпендикулярно AC , ось z проходит через точку A, пер-
пендикулярно плоскости ABC (см. рис.11). Тогда вершины пирамиды имеют координаты: А(0; 0; 0); В(- ; ; 0); С(0; ;0), Д (а; ;0), Е( ; ; 0), F(а;0;0),М( ; ; h).
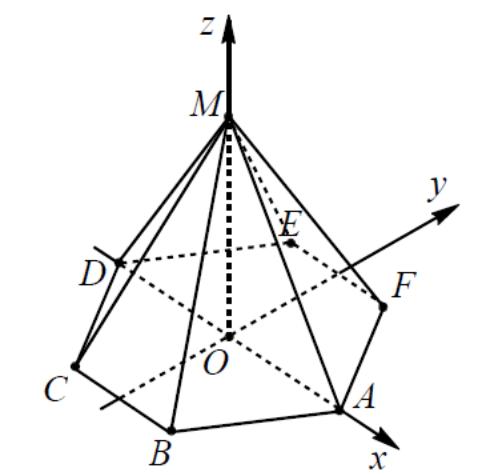
6.2 Еще один вариант расположения правильной шестиугольной пирамиды относительно прямоугольной декартовой системы координат показан на рисунке 12.
Рисунок №1 |
|
Р |
Рисунок №4 |
|
|
Рисунок №7
|
|
Рисунок №9
|
|
Рисунок №11
|
|

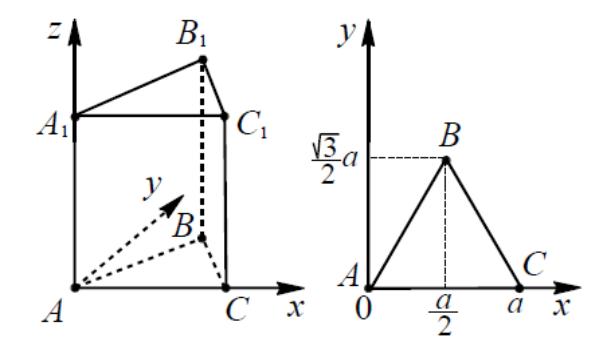 Рисунок
№2
Рисунок
№2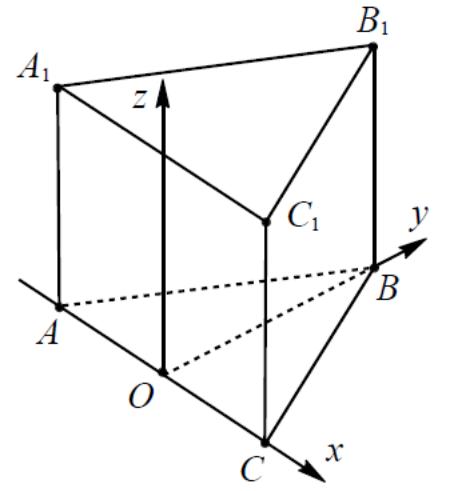 исунок
№3
исунок
№3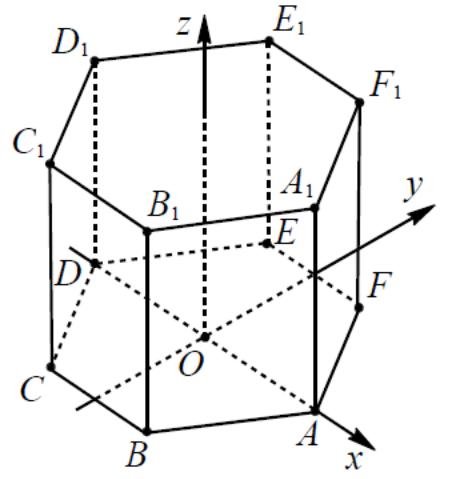 Рисунок
№5
Рисунок
№5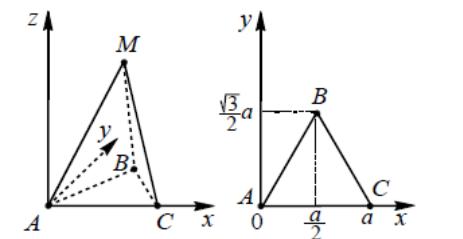 Рисунок
№6
Рисунок
№6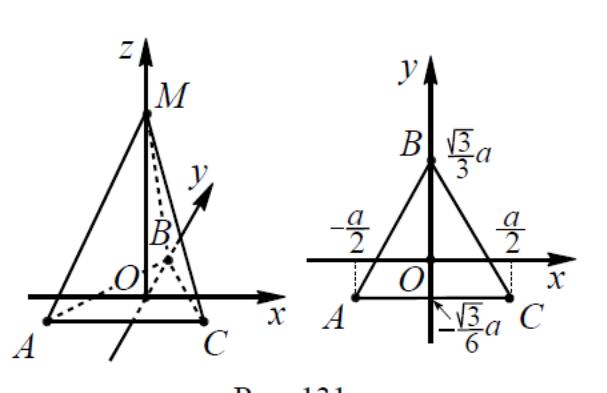
 Рисунок
№8
Рисунок
№8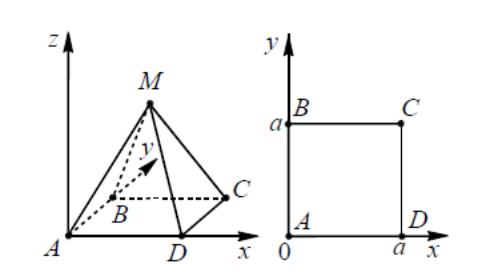
 Рисунок
№10
Рисунок
№10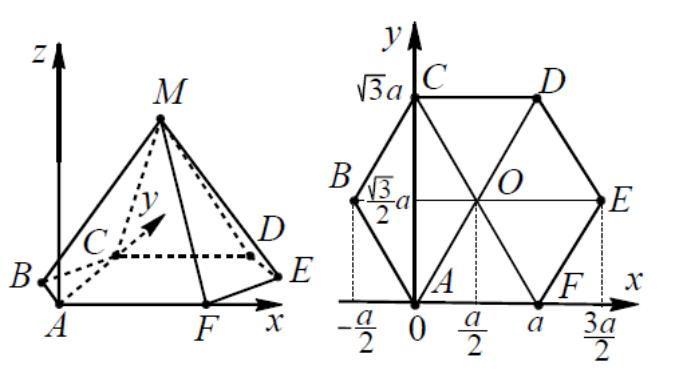
 рисунок
№12
рисунок
№12