- •1. Введение
- •2. Теоретическая часть: Методы решения стереометрических задач.
- •2.1 Поэтапно-вычислительный метод.
- •2.2 Координатный метод
- •Практическая часть.
- •3.1. Расстояние между двумя точками.
- •3.2. Расстояние от точки до прямой
- •3.3. Расстояние от точки до плоскости
- •3.4. Угол между двумя прямыми
- •4.Заключение.
- •5.Приложения
- •2. Правильная треугольная призма
- •3.Правильная шестиугольная призма
- •4. Правильная треугольная пирамида
- •5. Правильная четырехугольная пирамида
- •6. Правильная шестиугольная пирамида
4.Заключение.
1. При решении задач на нахождение расстояния между двумя точками и нахождения расстояния от точки до прямой поэтапно – вычислительный метод более рациональный, так как вычислительный аппарат обоих методов практически одинаков, но при координатном методе необходимо дополнительно найти координаты точек, вычислить длины отрезков, что можно сделать быстрее поэтапно – вычислительным способом.
2. При решении задач на нахождение расстояния от точки до плоскости и нахождении угла между прямыми в более простых задачах оба способа примерно равноценны, но при усложнении условия преимущества координатного способа очевидны. Владея координатным способом можно решить любую задачу данного блока изобразив многогранник, построив сечение и введя систему координат.
5.Приложения
Приложение .№1.
Рисунок №1.
|
|
|
|
|
|
Рисунок
№7 |
Рисунок
№8 |
Рисунок
№9 |
Приложение №2.
Координаты вершин некоторых многогранников, часто используемых при решении задач. 1. Куб
1.1.Куб АВСД с ребром a . Пусть начало координат находится в точке A , направление координатных осей показано на рис1. Тогда вершины куба имеют координаты: A(0; 0; 0) , B(0; a; 0) , C(a; a; 0) ,D(a; 0; 0) , (0;0;а); (0; а;а); (а;а;а); (а;0;а)
1.2.Такое же расположение системы координат удобно использовать для прямоугольного параллелепипеда. Еще один вариант расположения прямоугольного параллелепипеда (куба) относительно декартовой системы координат связан с размещением начала координат в точке пересечения диагоналей основания.
2. Правильная треугольная призма
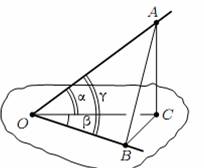
2.1. Правильная треугольная призма АВС , сторона основания которой равна a , а боковое ребро b . Пусть начало координат находится в точке A , ось x направлена вдоль ребра AC , ось y про- ходит через точку A перпендикулярно AC , ось z направлена вдоль
бокового ребра А (см. рис. 2). Тогда вершины призмы имеют координаты: А(0; 0; 0);
В(
 ;
;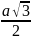 ;
0); С(а; 0; 0),
(0;
0; b),
(
;
;
b),
(а;0;
b)
;
0); С(а; 0; 0),
(0;
0; b),
(
;
;
b),
(а;0;
b)
2.2 Другой вариант расположения правильной треугольной призмы относительно прямоугольной декартовой системы координат показан на рисунке №3.
3.Правильная шестиугольная призма
3.1
Правильная
шестиугольная призма ABCDEF
,
сторона основания которой равна a
,
а боковое ребро
b
.
Пусть начало координат находится в
точке
A
,
ось x
направлена
вдоль ребра
AF
,
ось y
проходит
через точку A
перпендикулярно
AF,
ось z
направлена
вдоль
бокового ребра 1 AA
(см.
рис. 4).
Тогда
вершины призмы имеют координаты: А(0; 0;
0); В(-
;
;
0); С(0; ;0),
Д (а;
;0),
Е(
;0),
Д (а;
;0),
Е(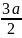 ;
;
0), F(а;0;0),
(0;0;b),
(-
;
;
b);
(0;
;
b),
(а;
;
b),
(
;
;
b),
(а;0;b)
;
;
0), F(а;0;0),
(0;0;b),
(-
;
;
b);
(0;
;
b),
(а;
;
b),
(
;
;
b),
(а;0;b)
3.2. Другой вариант расположения правильной шестиугольной призмы относительно прямоугольной декартовой системы координат представлен на рисунке№5

 Рисунок
№2
Рисунок
№2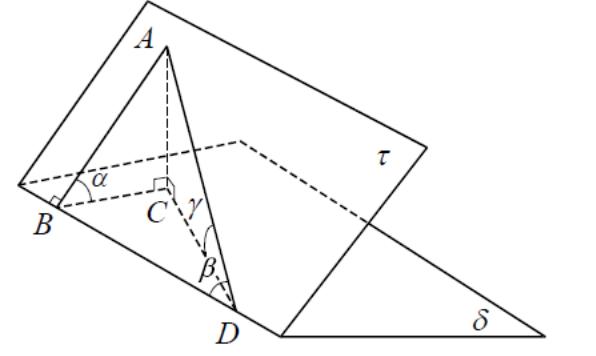 Рисунок
№3
Рисунок
№3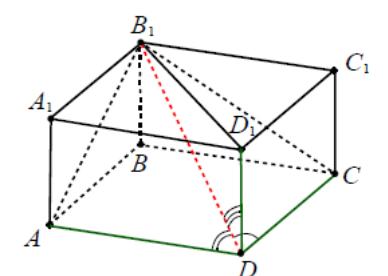 Рисунок
№4
Рисунок
№4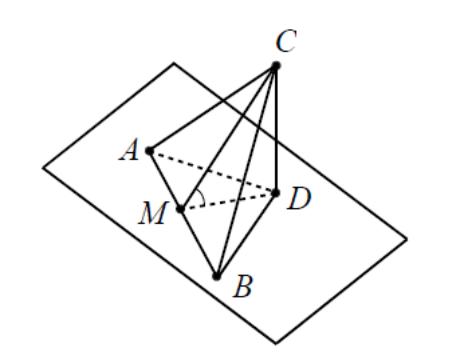 Рисунок
№5
Рисунок
№5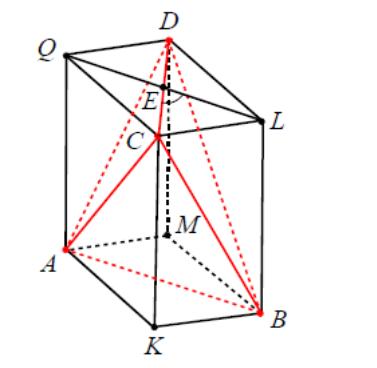 Рисунок
№6
Рисунок
№6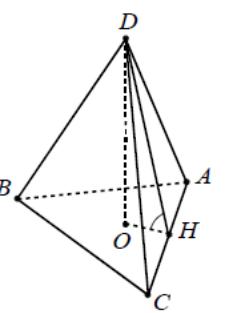 7
7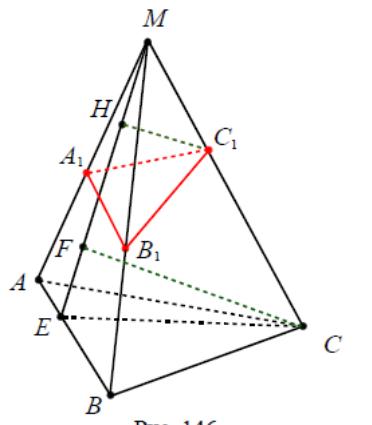 8
8