3.3. Расстояние от точки до плоскости
Расстояние от точки до плоскости, не содержащей эту точку, есть длина отрез-
ка перпендикуляра, опущенного из этой точки на плоскость.
Расстояние между прямой и параллельной ей плоскостью равно длине их общего перпендикуляра.
Расстояние между прямой и параллельной ей плоскостью равно расстоянию от любой точки этой прямой до плоскости.
Расстояние между двумя параллельными плоскостями равно длине их общего перпендикуляра.
Расстояние между двумя параллельными плоскостями равно расстоянию между точкой одной из этих плоскостей и другой плоскостью.
поэтапно-вычислительный метод
Расстояние от точки M до плоскости α
1) равно расстоянию до плоскости α от произвольной точки P , лежащей на прямой l , которая проходит через точку M и параллельна плоскости α;
2) равно расстоянию до плоскости α от произвольной точки P , лежащей на плоскости β , которая проходит через точку M и параллельна плоскости α.
Координатный метод.
Расстояние от точки М до плоскости α можно вычислить по формуле
(М,
)
=
,
где М (
).
Плоскость α задана уравнением
ах+bу+сz+d=0.
Пример 1. В единичном кубе АВСД найти расстояние от точки до плоскости А С
Решение.
Поэтапно-вычислительный метод. Решим
задачу методом вспомогательного объема.
=
*
H;
=
*АВ.
Объемы этих пирамид равны, поэтому имеем
H
=
.
правильный со стороной равной
.
=
.
=
;
АВ= 1.
H
=
=
.
Ответ.
.
Координатный метод. Введем систему координат таким образом, что ось абсцисс пойдет по АД, ось ординат по ДС, ось аппликат по Д . Расстояние от точки до плоскости А С можно вычислить по формуле
(
,
)
=
,
где М (
).
Плоскость А
С
задана уравнением ах+bу+сz+d=0. А(1,0,0), С(
0,1,0),
(1,1,1),
(0,1,1).
Подставим координаты точек плоскости
А
С
в уравнение плоскости. а+d=0;
b
+ d
=0; a
+b
+c
+ d
=0 .
а
= - d,
b
= - d,
c
=d.
Составим уравнение плоскости А
С:
-dx
–dy
+dz
+d
=0, x
+y
–z
– 1 =0 . По формуле находим расстояние
от точки до плоскости
(
,
)
=
=
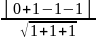. Ответ.
.
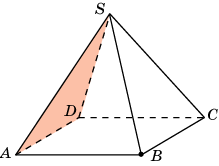
Пример2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от точки B до плоскости SAD.
Решение.
Поэтапно
– вычислительный метод.
Решим задачу методом вспомогательного
объема.
=
*BH,
=
*SO,
где
SO
АBD.
BH =
.
=
=
.
SO
=
.
BH
=
=
.
Ответ.
Координатный
метод.
Введем систему координат таким образом:
ось абсцисс пойдет по АД, ось ординат
по ДС, ось аппликат через точку Д
АДСВ.
А(1,0,0), Д ( 0,0,0), S
(
;
;
),
В(1,1,0). Подставим координаты точек А, Д,
S
в уравнение плоскости: .
а+d=0,
d
=0 ,
a
+
b
+
c
+d
=0, а
= - d,
d
= 0, b
= -
c,
Составим уравнение плоскости -
cy
+ cz
= 0, -
y
+ z
=0. По формуле находим расстояние от
точки до плоскости
(B,
)
=
=
.
Ответ.
.
3.4. Угол между двумя прямыми
Углом между двумя пересекающимися прямыми называется наименьший из уг-
лов, образованных при пересечении прямых.
<
(a,
^b)
≤
.Углом между скрещивающимися прямыми называется угол между пересекаю-щимися прямыми, соответственно параллельными данным скрещивающимся.
Две прямые называются перпендикулярными, если угол между ними равен .
Угол между параллельными прямыми считается равным нулю.
поэтапно-вычислительный метод
При
нахождении угла α между прямыми m
и
l
используют
формулу
=
где a и b,с - длины сторон треугольника АВС, соответственно параллельных этим прямым.
координатный метод Угол α между двумя векторами } и вычисляется по формуле: cos =
Для
того, чтобы векторы были перпендикулярны
необходимо и достаточно, чтобы
=0,
т.е
=0
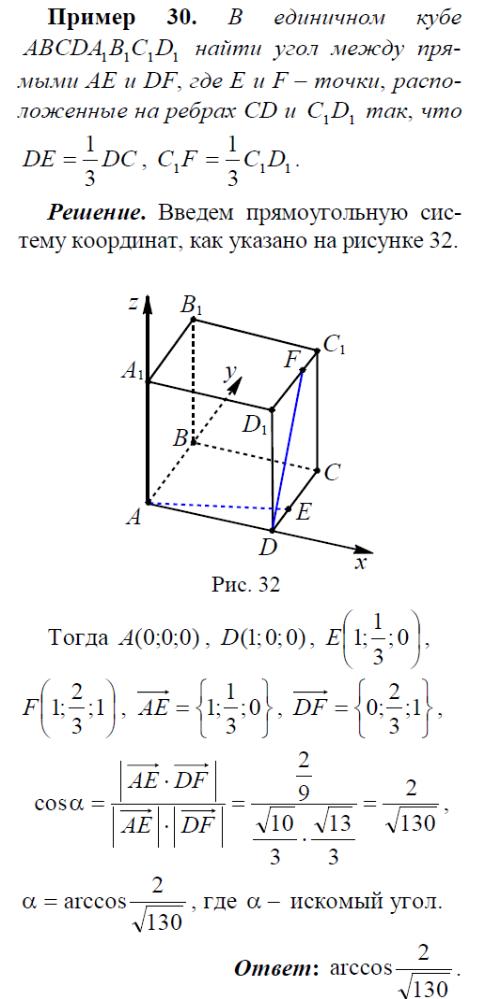
Пример
1. В
единичном кубе АВСД
найти угол между прямыми АЕ и DF,
где
Е и F – точки,
расположенные
на ребрах CD и
так,
что
ДЕ=
ДС,
=
.
Решение.
1. Поэтапно – вычислительный метод.
Параллельным
переносом совместим DF
и АЕ, получим ∆АЕ
.
АЕ=
.
А
=
.
Е
=
.
По теореме косинусов из ∆АЕ
имеем: cos
EA
=
=
.
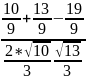EA
=
arccos
.
Ответ.
arccos
.
Координатный
метод. Введем
прямоугольную систему координат, как
показано на рисунке. Тогда А(0,0,0), Д(1,0,0),
Е(1,
,
0), F(1,
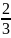,1).
{1.
,
0},
{0,
,
1}, cos
α
=
.
cos
α=
=
.
α
= arccos
.
Ответ. arccos
.
Пример
2.В
правильной шестиугольной призме ABCDEF
,
все ребра которой равны 1, найдите косинус
угла между прямыми А
и
В
.
Решение.
Координатный метод. Введем
систему координат, как показано на
рисунке. А(0,0,0),
(-
;
;
1); В (-
;
;
0),
(0;
;
1),
{-
;
;
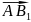1},
{
,
,
1}. сos
α
=
.
сos
α
=
.
Ответ.
.