
- •1. Введение
- •2. Теоретическая часть: Методы решения стереометрических задач.
- •2.1 Поэтапно-вычислительный метод.
- •2.2 Координатный метод
- •Практическая часть.
- •3.1. Расстояние между двумя точками.
- •3.2. Расстояние от точки до прямой
- •3.3. Расстояние от точки до плоскости
- •3.4. Угол между двумя прямыми
- •4.Заключение.
- •5.Приложения
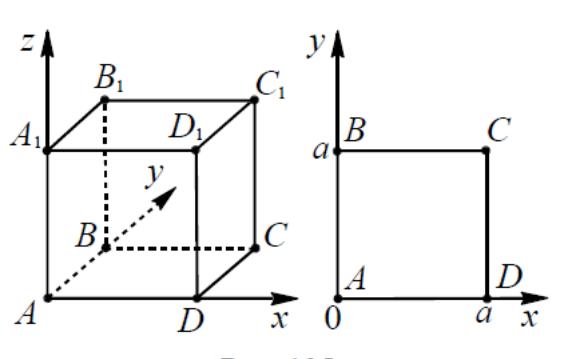
- •2. Правильная треугольная призма
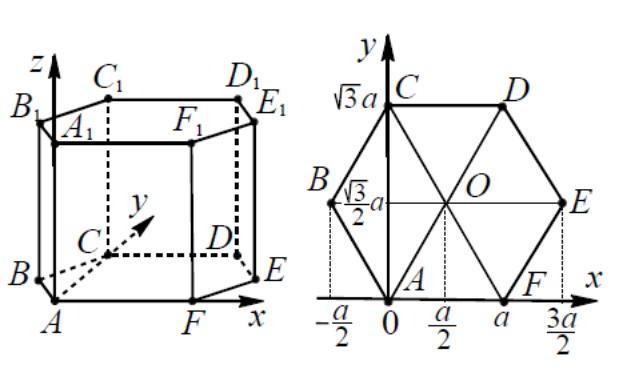
- •3.Правильная шестиугольная призма
- •4. Правильная треугольная пирамида
- •5. Правильная четырехугольная пирамида
- •6. Правильная шестиугольная пирамида
2.2 Координатный метод
Координатный метод является естественным продолжением векторного метода, то есть вектор пространства есть упорядоченная тройка действительных чисел (декартовых прямоугольных координат вектора в ортонормированном базисе). Рациональное расположение фигуры относительно системы координат (некоторые вершины многогранника находятся на координатных осях), позволяет при решении задач упростить вычисления.
Основные формулы, применяемые при решении задач координатным методом:
Р
 асстояние
между двумя т очками можно вычислить
по формуле:
асстояние
между двумя т очками можно вычислить
по формуле:Ρ(А,В) =
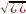 ,
где А(
,
где А(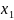 ;
;
),
B(
;
;
),
B(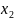 ;
;
).
;
;
).
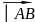 │=
│=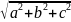 ,
где {a, b, c} координаты вектора
,
где {a, b, c} координаты вектора
 .
.Расстояние от точки М до плоскости
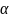 можно вычислить по формуле
можно вычислить по формуле
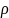 (М,
)
=
(М,
)
= ,
где М (
,
где М ( ).
Плоскость
задана уравнением ах+bу+сz+d=0.
).
Плоскость
задана уравнением ах+bу+сz+d=0.
Угол
 между двумя векторами
между двумя векторами
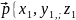 }
и
}
и
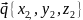 вычисляется по формуле:
вычисляется по формуле:
cos
=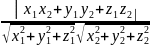
координаты вершин некоторых многогранников, часто используемых при решении задач, приведены в приложении №2
Практическая часть.
3.1. Расстояние между двумя точками.
Основные теоремы, применяемые при нахождении расстояния между двумя точками – теорема Пифагора, теорема косинусов.
Основные формулы, применяемые при решении задач координатным методом:
Р асстояние между двумя т очками можно вычислить по формуле:
Ρ(А,В) = , где А( ; ; ), B( ; ; ). │= , где {a, b, c} координаты вектора .
 П
ример
1.Ребра
правильной четырехугольной призмы
равны 1, 4 и 4. Найдите расстояние от
вершины до центра основания призмы, не
содержащего эту вершину.
П
ример
1.Ребра
правильной четырехугольной призмы
равны 1, 4 и 4. Найдите расстояние от
вершины до центра основания призмы, не
содержащего эту вершину.
 Решение.
Поэтапно вычислительный метод. АС
=4
Решение.
Поэтапно вычислительный метод. АС
=4 , АО=2
,
О=
, АО=2
,
О=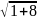 =3
Координатный метод.
(0,0,1),
О (2,2,0)
О
=
=3
=3
Координатный метод.
(0,0,1),
О (2,2,0)
О
=
=3
Пример
2.
.В правильной шестиугольной призме
ABCDEF

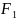 ,
все ребра которой равны 1, найдите
расстояние между точками A
и
.
Решение.
Поэтапно вычислительный метод. АЕ
=
,
все ребра которой равны 1, найдите
расстояние между точками A
и
.
Решение.
Поэтапно вычислительный метод. АЕ
=
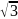 ,
(По теореме косинусов из ∆ AEF),
А
=
2. Ответ. 2
,
(По теореме косинусов из ∆ AEF),
А
=
2. Ответ. 2
Координатный
метод. А(0,0,0),
( ;
;
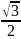 ;1),
А
=
;1),
А
=
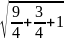 =
2. Ответ. 2
=
2. Ответ. 2
3.2. Расстояние от точки до прямой
Расстояние от точки до прямой, не содержащей эту точку, есть длина отрезка перпендикуляра, проведенного из этой точки на прямую.
Расстояние между двумя параллельными прямыми равно длине отрезка их общего перпендикуляра.
Расстояние между двумя параллельными прямыми равно расстоянию от любой точки одной из этих прямых до другой прямой.
поэтапно-вычислительный метод
1.Расстояние
от точки до прямой можно вычислить, как
длину отрезка перпендикуляра, если
удается включить этот отрезок в некоторый
треугольник в качестве одной из высот.
2. Еще один подход к нахождению расстояния
от точки А до прямой а состоит в том,
чтобы найти основание
 перпендикуляра, опущенного из точки А
на прямую а. Если точка
находится
вне участка прямой а, данного в задаче,
то через точку А проводят прямую с,
параллельную а, и выбирают на ней более
удобную точку С, ортогональная проекция
которой
перпендикуляра, опущенного из точки А
на прямую а. Если точка
находится
вне участка прямой а, данного в задаче,
то через точку А проводят прямую с,
параллельную а, и выбирают на ней более
удобную точку С, ортогональная проекция
которой
 принадлежит данному участку прямой а.
принадлежит данному участку прямой а.
 Пример
1.
1. В кубе A…D1, все ребра которого равны
1, найдите расстояние от точки B до прямой
AC1.
Пример
1.
1. В кубе A…D1, все ребра которого равны
1, найдите расстояние от точки B до прямой
AC1.
Р
ешение.
1 способ. Поэтапно-вычислительный.
1. Построим вспомогательный
 АВ
АВ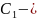 прямоугольный (АВ
прямоугольный (АВ
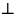 ВС, следовательно, по теореме о трех
перпендикулярах В
ВС, следовательно, по теореме о трех
перпендикулярах В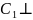 АВ). По
свойству диагонали куба имеем: А
АВ). По
свойству диагонали куба имеем: А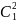 = 3А
= 3А , А
=
. АВ=1, В
=
. 2. В прямоугольном треугольнике АВ
найдем высоту, проведенную из
вершины прямого угла, длина которой
является расстоянием от точки В до
прямой AC1. ВН=
, А
=
. АВ=1, В
=
. 2. В прямоугольном треугольнике АВ
найдем высоту, проведенную из
вершины прямого угла, длина которой
является расстоянием от точки В до
прямой AC1. ВН=
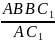 , ВН=
, ВН=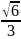 .
.
 2
способ. Координатный.
Введем прямоугольную систему координат:
ось абсцисс пойдет по прямой АД, ось
ординат по ДС, ось аппликат по прямой
Д
.
Тогда В(1;1;0), C1(0;1;1),
А(1;0;0).
2
способ. Координатный.
Введем прямоугольную систему координат:
ось абсцисс пойдет по прямой АД, ось
ординат по ДС, ось аппликат по прямой
Д
.
Тогда В(1;1;0), C1(0;1;1),
А(1;0;0).
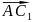 {-1;1;1},
{-1;1;1},
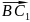 {-1;0;1},
{
0;1;0}, │
│=
,
│
│=
,
│
│=1,
По теореме косинусов из ∆ А
В
cos A
B
=
,
sin
A
B=
{-1;0;1},
{
0;1;0}, │
│=
,
│
│=
,
│
│=1,
По теореме косинусов из ∆ А
В
cos A
B
=
,
sin
A
B=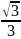 ,
BH=
. Ответ.
.
,
BH=
. Ответ.
.
Пример 2. В правильной треугольной призме ABC , все
ребра которой равны 1, найдите расстояние от точки B до прямой A .
Решение.
1 способ. Поэтапно-вычислительный.
1. Построим вспомогательный
АВ
.
АВ=1, В
=
,
А
=
.
По теореме косинусов cos
A
B=
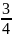 ,
sin
A
B=
,
sin
A
B=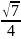 .
.
 =
В
А
sin
A
B,
=
.
=
A
*
BH, BH=
=
В
А
sin
A
B,
=
.
=
A
*
BH, BH=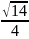 .
.
2
способ. Координатный.
Введем
систему координат таким образом: ось
аппликат пойдет по прямой А
,
ось ординат по прямой АВ, ось абсцисс
АВ. Тогда А(0;0;0), В(0;1;0),
(
;
;
1).
{0; 1;0},
{
;
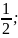 1},
{
;
1},
{
;
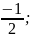 1}, │
│=1,
│
│=
,
│
1}, │
│=1,
│
│=
,
│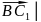 =
.
По теореме косинусов cos
AC1B=
,
sin
AC1B=
.
=
.
По теореме косинусов cos
AC1B=
,
sin
AC1B=
.
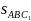 =
В
А
sin
AC1B,
=
.,
.
=
AC1
BH,
BH=
.Ответ.
.
=
В
А
sin
AC1B,
=
.,
.
=
AC1
BH,
BH=
.Ответ.
.
