2.3.2. Визначення робочої висоти насадки

Поверхня контакту фаз із основного рівняння масопередачі визначається виразом

, (2.21)

де

– середня рухома сила процесу, яка виражена в концентраціях газової фази.

Із рівняння (2.10) елементарна поверхня масопередачі рівняється

. (2.22)

Інтегруючи в межах зміни концентрації газу від y_п до y_к і поверхні контакту фаз від нуля до F одержимо

. (2.23)

Зважаючи, що

F=H_нас·S·a

і

K_y·a=K_yv,

де

Н_нас – робоча висота насадки, м;

S – площа поперечного перерізу колони, м²;

a – питома поверхня насадки, м²/м³;

K_yv – об’ємний коефіцієнт масопередачі, який виражений в концентраціях газової фази,

робоча висота насадки буде рівна

. (2.24)

Позначимо інтеграл в рівнянні (2.24) через

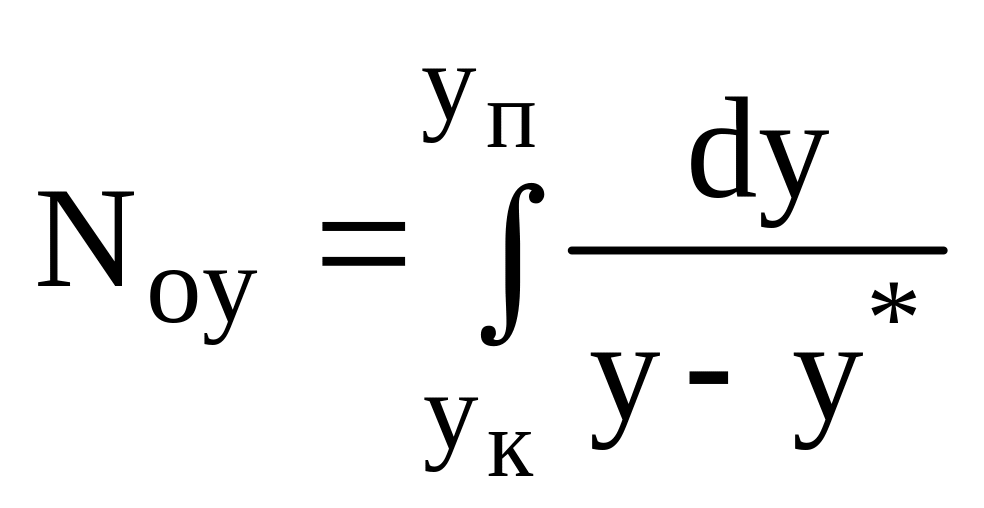. (2.25)

Величина N_oy зветься числом одиниць переносу (ЧОП), яке виражене в концентраціях газової фази

. (2.26)

Загальний матеріальний баланс по газовій фазі має вигляд

, (2.27)

звідки

. (2.28)

Підставляючи (2.28) в (2.23), одержимо

. (2.29)

Зіставляючи вирази (2.21) і (2.29) виявимо, що

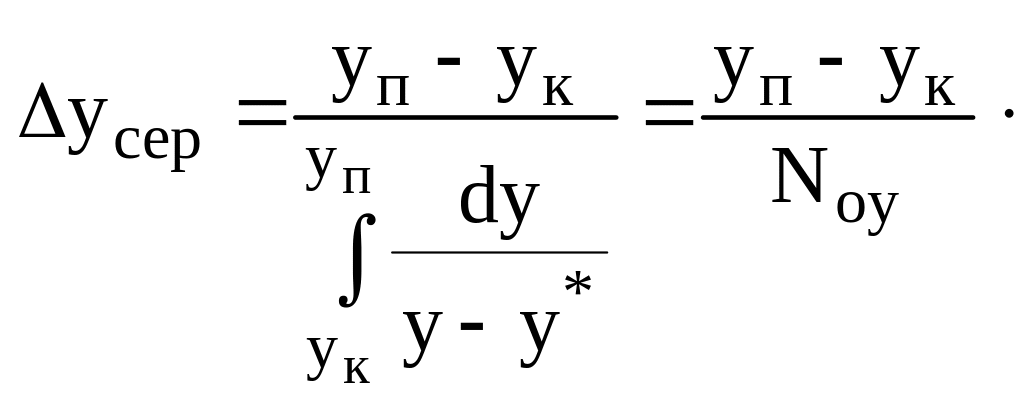(2.30)

Звідси

(2.31)

– представляє собою відношення різниці концентрацій до середньої рушійної сили. Відповідно до цього одиницю переносу можна розглядати як висоту насадки апарата, в якому різниця концентрацій в одній із фаз дорівнює середній рушійній силі. Число одиниць переносу слугує аналогом рушійній силі і характеризує ступінь розділу і виражає статику процесу масопередачі.

Аналогічно міркуючи можна одержати ЧОП, виражене в концентраціях рідкої фази

, (2.32)

. (2.33)

Перший множник в рівнянні (2.24)

(2.34)

– відповідає висоті насадки в апараті, для якої число одиниць переносу рівне одиниці, і зветься висотою одиниці переносу (ВОП), вираженою в концентраціях газової фази. ВОП є аналогом об’ємного коефіцієнта масопередачі і характеризує інтенсивність масопередачі в апараті і виражає кінетику процесу масопередачі. h_oy – обернено пропорційна об’ємному коефіцієнту масопередачі. Чим вище інтенсивність передачі маси в апараті, тим менше ВОП. Вимірюється в одиницях висоти. Аналогічно ВОП, яка виражена в концентраціях рідкої фази визначається виразом

. (2.35)

Звідси робочу висоту насадки визначають із рівняння

. (2.36)

Якщо число одиниць переносу визначається інтегралом, який неможливо розв’язати аналітично (тому що у більшості випадків невідома аналітична функція залежності у*=f(x) або x^*=f(y)), то для вирішення N_Oy и N_Ox застосовують графічний метод.

Розрахувати число одиниць переносу можна застосувавши чисельний метод Сімпсона (метод графічного інтегрування). За цим методом відрізок (y_п – y_к) поділяють на два рівні відрізки і визначають значення аргументу y_п, y₁ і y_к. За значенням аргументу знаходять значення функції , відповідно рівні , і . ЧОП в координатах – у від y_п до y_к є площа під кривою лінією (див. рис. 2.3). Згідно з методом Сімпсона ЧОП розраховують з рівняння

. (2.37)

Рис. 2.3. Визначення ЧОП. Пояснення див. в тексті.

Розрахунок ЧОП по (2.37) за трьома значеннями функції дає задовільний результат, якщо . При більшому значенні цього відношення необхідно проводити розрахунок, поділивши відрізок (y_п, y_к) на чотири рівні відрізки. Тоді ЧОП

(2.38)

В загальному випадку висота одиниці переносу залежить від гідродинамічного режиму, типорозміру насадки і від фізико-хімічних властивостей контактуючих фаз.

Зв'язок між загальною висотою одиниці переносу h_оy або h_оx і висотами одиниць переносу в фазах h_y и h_x виражається рівняннями

, (2.39)

, (2.40)

де

G – витрата газу, кмоль/год;

L – витрата рідини, кмоль/год;

m_ух – константа фазової рівноваги.

Насадкові апарати можуть працювати в різних гідродинамічних режимах, як в плівковому режимі, так і в режимі підвішування. Плівковий режим характеризується незначним впливом газу на стікаючу по насадці рідину і застосовується при обмеженні роботи колони по її гідравлічному опору. Якщо відсутнє обмеження, то бажано проводить процес абсорбції при активному зіткненні газу і рідини – режиму підвішування. Це сприяє збільшенню інтенсивності масообміну.

Розрахункове рівняння висоти одиниці переносу в рідкій фазі для плівкового режиму, яке охоплює велику кількість промислових насадок кільцевого і сідлообразного типу має вигляд [1]

, (2.41)

де

– критерій Рейнольдса для рідини; (2.42)

– дифузійний критерій Прандля для рідини; (2.43)

– приведена товщина плівки рідини, м; (2.44)

q – густина зрошення, м³/(м²·год);

ρ_х – густина рідини, кг/м³;

μ_х, – коефіцієнт динамічної в’язкості рідини, Па·с;

D_x, – коефіцієнт молекулярної дифузії в рідині, м²/с;

g – прискорення вільного падіння, м/с²;

W – приведена швидкість газу, м/с.

В режимі підвішування висоту одиниць переносу в рідкій фазі рекомендують [4] розраховувати по рівнянню

, (2.45)

де

– висота одиниці переносу при швидкості захлинання (інверсії фаз), яка визначається з рівняння [5]

. (2.46)

Коефіцієнти В і k наведені в таблиці 2.3.

Таблиця 2.3.

Значення коефіцієнтів В і k в рівнянні (2.46)

Насадка	Коефіцієнти
	В	k·103
Керамічні кільця Рашига 15х15х3 мм 25х25х4 мм 50х50х6 мм	2,88 3,12 2,24	4,77 4,77 0,62
Металеві кільця Палля 25х25х1 мм 50х50х1 мм 50х50х2 мм (пластмасові кільця Палля)	2,57 2,13 1,81	1,46 0,46 0,46

Відомо [2], що при турбулентному русі перенесення кількості руху і речовини здійснюється однаковими механізмами і описується однотипними рівняннями. В цьому разі рекомендують [4] висоту одиниці переносу в газовій фазі розраховувати з рівняння

, (2.47)

де

Ψ – коефіцієнт, рівний відношенню коефіцієнту дифузії газу D_т до коефіцієнта в’язкості газу ν_т при турбулентному русі, який можна прийняти рівним одиниці;

λ – коефіцієнт тертя, який рівний λ_підв≈0,08 – для точки підвішування і λ_з≈0,1 – для точки захлинання (інверсії фаз).

Якщо визначить висоти одиниці переносу в газовій фазі при швидкостях підвішування і захлинання , то легко знайти висоту одиниці переносу при будь-якій швидкості газу, оскільки залежність lg(h_y/(Pr_y′)^2/3=f[lg(W/W_з)] лінійна. Pr_y′ - дифузійний критерій Прандля для газової фази, який знаходять з рівняння

, (2.48)

де

μ_у – коефіцієнт динамічної в’язкості газу, Па∙с;

ρ_у – густина газу, кг/м³;

D_y – коефіцієнт дифузії в газі, м²/с.