5. Вычисление приращения функции с помощью производной

Из определения производной (3) следует, что приращение функции Δf, обусловленное малым приращением аргумента Δх, можно приближенно представить в виде Δf ≈ . Это равенство выполняется тем точнее, чем меньше Δх. Если взять бесконечно малое приращение аргумента Δх, последнее соотношение станет точным. Приращение функции Δf при этом тоже станет бесконечно малым. Чтобы отличать бесконечно малое (или элементарное) приращение аргумента и функции от конечного приращения, их обозначают соответственно dx и df. Ясно, что элементарное приращение функции находится по формуле

. (7)

П р и м е р 6. Тело брошено с начальной скоростью v₀=20,0м/с. Его высота над уровнем земли меняется по закону v₀t-gt²/2 g=9,81м/с². Определить перемещение Δh тела за промежуток времени Δt=10,0мс, происшедшее после первой секунды движения.

Считая Δt малым, найдем Δh по приближенной формуле

(v₀-gt)Δt=(20,0-9,81·1,00)·0,01=0,1019м.

Точное вычисление по формуле дает результат Δh=0,10151м. Отличие обоих результатов сказывается только в четвертой значащей цифре. Исходные данные приведены с тремя значащими цифрами, следовательно, оба результата практически совпадают.

6.Приближенное вычисление площади под графиком фукции.

Интегральная сумма

На рис. 4 изображен график функции у=f(х), причем f(х)>0. Требуется найти площадь фигуры, ограниченной сверху графиком функции f(х), слева и справа – отрезками прямых, проведенных через точки х=а и х=b параллельно оси ординат, снизу – осью х.

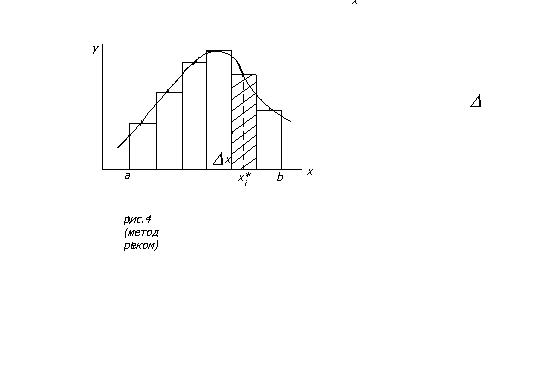
Рис.4 К понятию определенного интеграла

Для вычисления площади разобьем участок оси х между точками а и b на n отрезков длиной Δх₁ Δх₂… Δх_n. Построим n прямоугольников с основаниями соответственно Δх₁ Δх₂… Δх_n и высотами f(х₁^*), f(х₂^*),… f(х_n^*), где х_i^* - любая точка, лежащая внутри отрезка оси х с номером i(i=1, 2,…n). Ясно, что искомая площадь S приближенно равна сумме площадей прямоугольников. Площадь прямоугольника с номером i очевидно равна , следовательно,

. (8)

Выражение, стоящее в правой части формулы (8), называется интегральной суммой. Приближенное равенство в формуле (8) будет выполняться тем точнее, чем меньше отрезки Δх_i.

7. Точное вычисление площади под графиком функции.

Определенный интеграл

Чтобы получить точное выражение для площади S, следует взять предел выражения (8), устремив длины всех отрезков Δх_i к нулю:

. (9)

Очевидно, что число слагаемых в сумме (9) при этом будет стремиться к бесконечности.

Таким образом, вычисление площади под графиком функции сводится к вычислению предела от интегральной суммы. Аналогично, вычисление многих физических величин часто сводится к вычислению предела некоторой интегральной суммы. Предел интегральной суммы (9) называется определенным интегралом от функции f(х) в пределах от а до b. Для обозначения определенного интеграла принята запись

. (10)

При этом полагают по определению =- .

Приведем пример, в котором необходимо использовать понятие интеграла.

П р и м е р 7. Известно, что плотность воздуха в атмосфере меняется с высотой h над уровнем моря по закону , где ρ₀-плотность воздуха на уровне моря, a=Mg/RT, M-относительная молекулярная масса воздуха, g-ускорение свободного падения, R-газовая постоянная, Т-абсолютная температура воздуха. Необходимо определить массу воздуха в столбе высотой Н и площадью основания S.

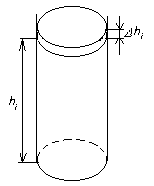
Рис.5 К примеру 7

Разобьем весь столб воздуха на элементарные слои толщиной Δh₁, Δh₂,… Δh_n, высота i-го слоя над уровнем моря составляет h_i , а его объем ΔV_i=SΔh_i (рис.5). Так как толщина слоя невелика, можно считать, что в пределах каждого слоя плотность воздуха практически постоянна, поэтому масса воздуха, заключенного в объеме ΔV_i, составляет , а масса воздуха во всем столбе

. (11)

В правой части формулы (11) стоит интегральная сумма. Если перейти к пределу Δh_i→0, то приближенное равенство станет точным, а интегральная сумма перейдет в интеграл:

. (12)

Этот интеграл будет вычислен в примере 9.