
- •(Государственный университет)
- •Приращение функции и вычисление средней скорости
- •Изменения функции
- •Производная, ее вычисление с помощью графика функции
- •Методика восстановления графика производной по графику функции
- •4. Производные элементарных функций.
- •5. Вычисление приращения функции с помощью производной
- •6.Приближенное вычисление площади под графиком фукции.
- •7. Точное вычисление площади под графиком функции.
- •8. Неопределенный интеграл. Выражение определенного
- •9. Простейшие правила и приемы интегрирования
- •Приращение функции и вычисление средней скорости
МОСКОВСКИЙ ИНЖЕНЕРНО-ФИЗИЧЕСКИЙ ИНСТИТУТ
(ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ)
Методические рекомендации
к использованию понятий
производной и интеграла
в курсе
ОБЩЕЙ ФИЗИКИ
МОСКВА
Министерство образования Российской Федерации
Министерство Российской Федерации по атомной энергии
Московский инженерно-физический институт
(Государственный университет)
Методические рекомендации
к использованию понятий
производной и интеграла
в курсе
ОБЩЕЙ ФИЗИКИ
Утверждено
советом факультета ЭТФ
Москва
Методические рекомендации к использованию понятий производной и интеграла в курсе общей физики. – М.: Изд. МИФИ,
Предназначены для студентов 1-го семестра МИФИ. Цель рекомендаций – в оказании методической помощи студентам при решении задач и освоении теоретического материала по физике, требующего использования понятий производной и интеграла.
Иллюстрируется методика составления интегральных сумм для вычисления физических величин. Содержатся сведения о простейших приемах интегрирования и дифференцирования и о свойствах производных и интегралов. Рекомендации подкрепляются конкретными примерами, часто встречающимися в физических приложениях. Справочный материал дается в минимально необходимом объеме.
Составитель: Е.И. Бабаджан
Приращение функции и вычисление средней скорости
Изменения функции
Одним из основных свойств, характеризующих функцию, является скорость ее изменения. Пусть аргумент х функции f(x) получил приращение Δх, т.е. начальное значение аргумента равно х, а конечное х+Δх. Вычислим приращение функции, обусловленное приращением аргумента:
![]() .
(1)
.
(1)
Приращение – алгебраическая величина, которую нельзя отождествлять с «увеличением». Действительно, если f(x+Δх)<f(x), то Δf(x)<0 и приращение отрицательно.
Средняя скорость изменения функции на участке от х до х+Δх, вычисляется по формуле:
![]() .
(2)
.
(2)
П р и м е р 1. Частица движется вдоль оси у. В момент времени t1=5,00с координата частицы составила у1=2,00м, в момент времени t2=8,00с у2=3,20м. Требуется найти среднюю скорость <vу> движения частицы в промежутке времени от t1 до t2.
Рассматриваем координату частицы как функцию времени у(t), тогда
<vу>![]() .
.
Вычисление приводит к ответу: <vу>=0,400м/с.
Замечание. Средняя скорость изменения как характеристика функции обладает существенным недостатком, который иллюстрируется рис.1. Как видно из рис.1, функции f1(x) и f2(x) получили одинаковые приращения при изменении аргумента от х до х+Δх, следовательно, одинаковыми будут и средние скорости изменения функций f1 и f2 на этом отрезке. Между тем, из графиков видно, что функция f2(х) меняется гораздо быстрее, резче, чем f1 (х).
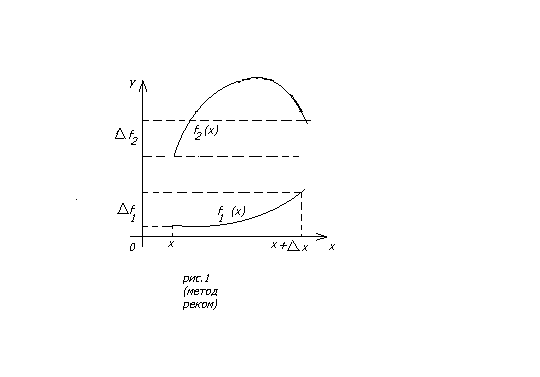
Рис.1. Графики двух различных функций, имеющих одинаковое приращение при изменении аргумента от х до Δх
Производная, ее вычисление с помощью графика функции
Предел отношения
Δf(х)/Δх
при Δх,
стремящемся к нулю, называется производной
функции f(х)
в точке х.
Для производной приняты обозначения
df/dx
или![]() .
Следовательно,
.
Следовательно,
f′(х)=limΔx→0![]() .
(3)
.
(3)
Как видно из рис.2, отношение Δf/Δх=tgα, где α -угол, образованный осью и прямой, проведенной через точки графика, соответствующие значениям х и х+Δх. При стремлении Δх к нулю точка 2 «скользит» по графику функции в направлении стрелки, приближаясь к точке 1. В результате прямая, проведенная через точки 1 и 2 будет приближаться к касательной, проведенной через точку 1 графика (см. пунктирную прямую на рис.2). Естественно, что производная будет численно равна тангенсу угла β, образованного касательной к графику в данной точке и осью х.
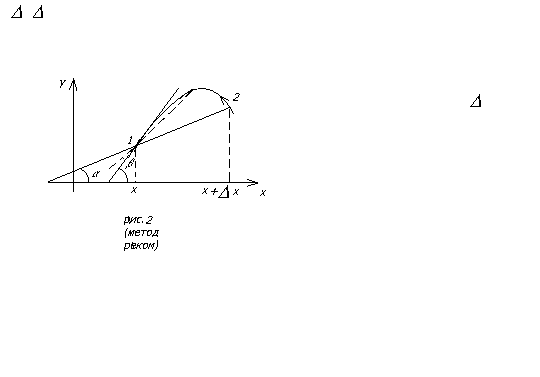
Рис.2 К геометрическому смыслу производной

Рис. 3 График функции f(х): а-график функции;
б-график производной
