
- •1. Подходы к определению понятия «система». Классификация и характеристика систем. Модель «черного ящика». Статические и динамические модели.
- •1 Класс моделей – это модели типа черного ящика.
- •2 Класс моделей – это модель состава системы.
- •3 Класс моделей – структурная схема системы.
- •2. Определение, обозначение, примеры нечеткого множества. Основные характеристики нечетких множеств.
- •3. Расширение понятия нечеткого множества
- •4. Стандартные операции над нечеткими множествами и их свойства. Расширенные операции над нечеткими множествами.
- •Стандартная функция дополнения
- •Нечеткое разбиение. (это лучше не писать!)
- •Нечеткое пересечение (fuzzy intersection).
- •Нечеткое объединение. Fuzzy union
- •5. Операции для определения различия между нечеткими множествами:
- •6. Показатели неопределенности (размытости) нечетких множеств.
- •7. Определение и свойства нечетких чисел. Декомпозиция нечеткого числа. Операции над нечеткими числами на основе интервального метода.
- •9. Определение нечетких отношений. Способы представления нечетких отношений.
- •10. Нечеткие графы. Разновидности нг. Нечеткие гиперграфы.
- •11. Операции над нечеткими отношениями. Свойства нечетких отношений. Транзитивное замыкание нечетких отношений.
- •12. Расширение понятия нечеткого отношения.
- •13. Нечеткое отношение эквивалентности, неэквивалентности, сходства, различия, предпорядка, порядка. Нечеткий гомоморфизм между нечеткими отношениями.
- •14. Понятие нечеткой переменной, понятие лингвистической переменной, логико-лингвистическая шкала.
- •15. Области применения нечетких моделей. Классификация нечетких моделей.
- •16. Определение нечеткой продукционной модели. Компоненты нечетких продукционных моделей.
- •17. Определение нечеткой продукционной модели. Компоненты нечетких продукционных моделей.
- •18. Определение нечеткой продукционной модели. Компоненты нечетких продукционных моделей. Классы операций нечеткой импликации. Критерии оценки нечеткой импликации
- •19. Основные задачи создания базы нечетких продукционных правил. Формирование нечетких (простых и составных) высказываний в предпосылках и заключениях правил.
- •20. Основные задачи создания базы нечетких продукционных правил. Классификация лингвистических продукционных правил.
- •21. Основные задачи создания базы нечетких продукционных правил. Классификация нечетких продукционных правил с заключениями в виде четких значений или функций.
- •22. Основные задачи создания базы нечетких продукционных правил. Типы структур базы нечетких продукционных правил (siso-, miso-, mimo-структуры).
- •24. Основные задачи создания базы нечетких продукционных правил. Каскадное соединение баз нечетких продукционных правил.
- •25. Основные задачи создания базы нечетких продукционных правил. Обеспечение полноты и непротиворечивости базы нечетких правил.
- •26. Основные компоненты нечетких продукционных моделей.
- •27. Алгоритмы нечеткого вывода Мамдани, Ларсена
- •27. Алгоритмы нечеткого вывода Цукамото, Такаги–Сугено.
9. Определение нечетких отношений. Способы представления нечетких отношений.
Нечетким
бинарным отношением
![]() между множествами A
и B
называется отображение
между множествами A
и B
называется отображение
![]() каждой
паре (a,b)
каждой
паре (a,b)![]() значение (степень принадлежности)
значение (степень принадлежности)
![]() ,
причем
,
причем
![]()
![]()
Аналогично
n-арное
нечеткое отношение-
пусть A1,A2,A3
…An
,
тогда
![]() может рассматриваться как множество
наборов элементов (a1,a2,a3
…an),
ai
может рассматриваться как множество
наборов элементов (a1,a2,a3
…an),
ai![]() с
функциями принадлежности µR(a1,a2,…,an)∊[0,1]
с
функциями принадлежности µR(a1,a2,…,an)∊[0,1]
С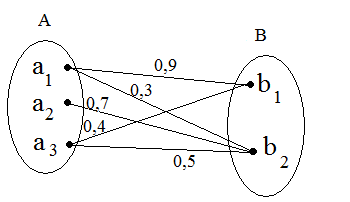 пособы
представления нечетких отношений:
пособы
представления нечетких отношений:
Взвешенные двудольные графы:
К
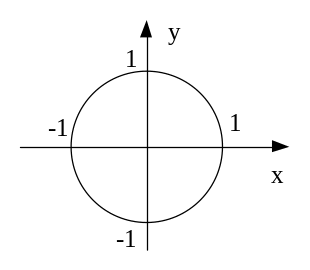 оординатными
диаграммами:
оординатными
диаграммами:
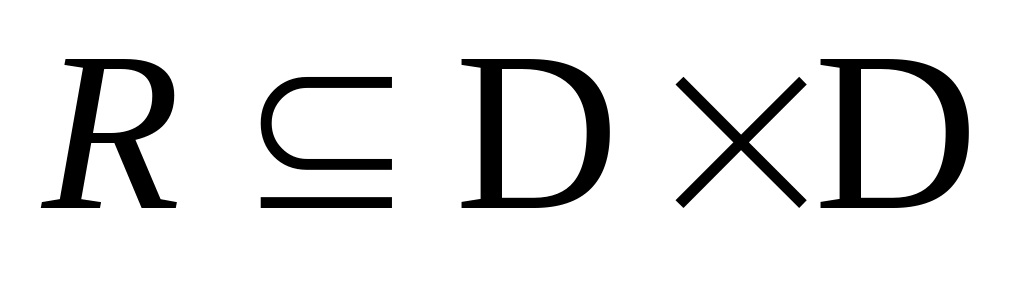 ,
где D
– множество действительных чисел.
Для
,
где D
– множество действительных чисел.
Для
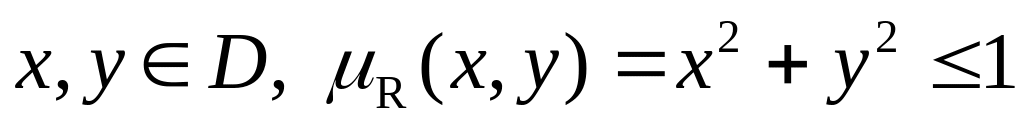
Матрицами:R
b1
b2
a1
0.9
0.3
a2
0,0
0.7
a3
0.4
0.5

A={a1, a2, a3}
B={ b1, b2}
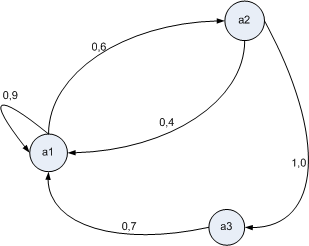
Взвешенный граф.
A={a1,a2,a3}
R={µR(a1,a1)=0.9,µR(a1,a2)=0.6, µR(a2,a1)=0.4, µR(a2,a3)=1.0, µR(a3,a1)=0.7}
Если симметрично, то может быть использован неориентированный граф. Дуги – связи в ориентированном графе, ребра – в неориентированном.
10. Нечеткие графы. Разновидности нг. Нечеткие гиперграфы.
Графы с нечеткими дугами
С нечеткими узлами и нечеткими дугами.
О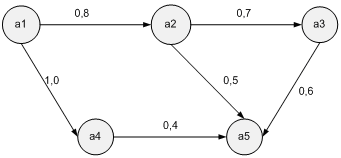 риентированным
нечетким графом с нечеткими дугами
риентированным
нечетким графом с нечеткими дугами
![]() ,
называется пара множеств, в которых
A={ai},
,
называется пара множеств, в которых
A={ai},![]() - множество вершин нечеткого графа,
- множество вершин нечеткого графа,
![]() - нечеткое множество дуг, причем вершина
ai
– начало, аj
– конец дуги.
- нечеткое множество дуг, причем вершина
ai
– начало, аj
– конец дуги.
![]() значение
функции для дуги.
значение
функции для дуги.
![]()
Пример:
G=(A,F)
A={a1, a2, a3, a4, a5}
F={0,8/( a1, a2); 0,7/( a2, a3); 1,0/( a1, a4); 0,5/( a2, a5); 0,4/( a4, a5); 0,6/( a3, a5);}
Вершины
ak
и al
графа
G=(A,F)
называются
нечетко смежными,
если существует дуга
![]() или
или
![]() ,
для которой
,
для которой
![]() или
или
![]() Это значение определяет степень смежности
вершины.
Это значение определяет степень смежности
вершины.
Вершины
ai
и
дуга
называются нечетко
инцидентными,
если
(ai=ak)
или (ai=al),
причем значение
![]() интерпретируется как степень инцидентности
дуги.
интерпретируется как степень инцидентности
дуги.
Нечеткие неориентированные графы.
Нечетким
неориентированным графом
![]() называется пара множеств, в которых
A={ai},
- множество вершин нечеткого графа,
называется пара множеств, в которых
A={ai},
- множество вершин нечеткого графа,
![]() - нечеткое множество дуг, в отличие от
ориентированного графа, порядок
следования i
и j
не имеет значения.
- нечеткое множество дуг, в отличие от
ориентированного графа, порядок
следования i
и j
не имеет значения.
Нечеткий ориентированный граф с нечеткими узлами и нечеткими дугами.
Нечетким
неориентированным графом с нечеткими
дугами и нечеткими вершинами
![]() называется пара множеств, в которых
называется пара множеств, в которых
![]() ={
={![]() },
},
- множество вершин нечеткого графа,
![]()
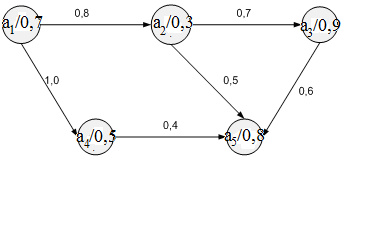
В общем виде связный нечеткий ориентированный граф называется нечеткой сетью.
Нечеткий
гиперграф
![]() ,
где
,
где
А – нечеткое множество его вершин, A={ai},
U –
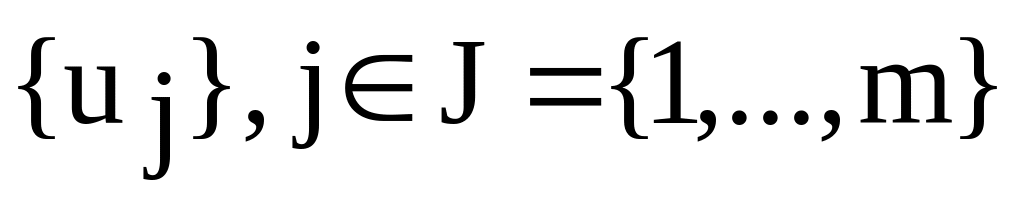
P – двуместный нечеткие предикат, который еще называется нечетким прецедентом, который определяется для всех пар, (ai,uj) и присваивает значение этой паре от 0 до 1.
Нечеткие гиперграфы являются адекватным представлением систем и процессов, в которых элементы связаны совокупностями различных n-арных нечетких отношений.
