4. Стандартные операции над нечеткими множествами и их свойства. Расширенные операции над нечеткими множествами.

Стандартные операции над нечеткими множествами и их свойства.

I Логические операции.

1) Включение

А и В – нечеткие множества на универсальном множестве Е. Говорят, что А содержится в В, если для

Иногда говорят, что множество А доминирует над В.

2) Равенство

Множества А и В равны, если для

3) Дополнение

Множества А и В дополняют друг друга, если для

4) Пересечение

Пересечением двух нечетких множеств А и В называют наибольшее нечеткое подмножество, содержащееся одновременно и в А, и в В.

Модой или модальным множеством для нечеткого множества А называют такое множество .

5) Объединение

Объединением двух нечетких множеств А и В называют наименьшее нечеткое подмножество, включающее как А, так и В, функция принадлежности которого:

6) Разность А-В

7) Дизъюнктивная сумма

У операций выполняются коммутативность, ассоциативность, идемпотентность, дистрибудивность, свойства с и теоремы де Моргана.

Не выполняются: .

I I Алгебраические операции

1) Алгебраическое произведение

2) Алгебраическая сумма

Для операций выполняются свойства коммутативности, ассоциативности, все свойства взаимодействия с пустым и универсальным множествами, теоремы де Моргана. Не выполняются идемпотентность, дистрибутивность.

Выполняются:

На основе операции алгебраического произведения, определяется операция возведения в степень нечеткого множества А, где > 0.

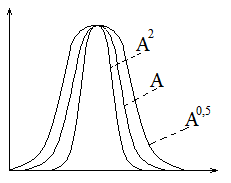
Операция концентрирования con(A)=A²

Операция растяжения dil(A)=A^0.5

3) Умножение нечеткого множества на число

4) Выпуклая комбинация нечетких множеств. Пусть у нас есть

тогда

5) Декартово произведение:

Пусть заданы НМ заданные на соответственно, тогда декартово произведение задано на множестве с функцией принадлежности:

Расширенные операции над нечеткими множествами.

1. Н

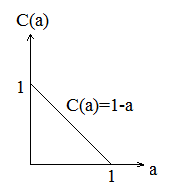
   Стандартная функция дополнения

   ечеткое дополнение (fuzzy complement) нечеткого множества А определяется одноместной функцией С:[0,1] -> [0,1]. Нечеткое дополнение удовлетворяет следующим аксиомам.

1. Ограниченность: С(0)=1, С(1)=0.

2. Аксиома монотонного невозрастания, если А< В, то С(А)>=С(B), для a,b [0,1] Эти 2 аксиомы называются аксиоматическим базисом для дополнения.

3. С

   

   - непрерывная функция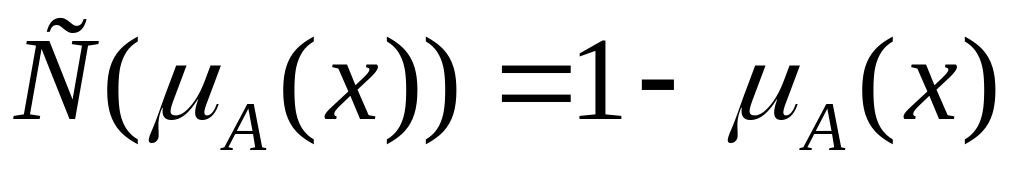

4. С(С(а))=а, для любого а из диапазона [1,0]

Функция дополнения Ягера (Yager)

Для значения функции w=1 вид функции дополнения прямая под 45 градусов, при увеличении значения w она будет стремиться к ступенчатому виду, и наоборот при уменьшении она будет приближаться к углу начала координат.

2. Нечеткое разбиение. (это лучше не писать!)

Совокупность нечетких множеств (А₁, А₂,…, А_n) на множестве Х, если выполнены следующие аксиомы:

1.

2.

3. …

3. Нечеткое пересечение (fuzzy intersection).

Нечеткое пересечение нечетких множеств А и В определенных на универсальном множестве Х, определяется двуместной функцией I:[0,1] -> [0,1], аргумент которой показывает включения элемента х, одновременно в множества А и В.

Свойства:

1. Ограниченность :

2. Коммутативность:

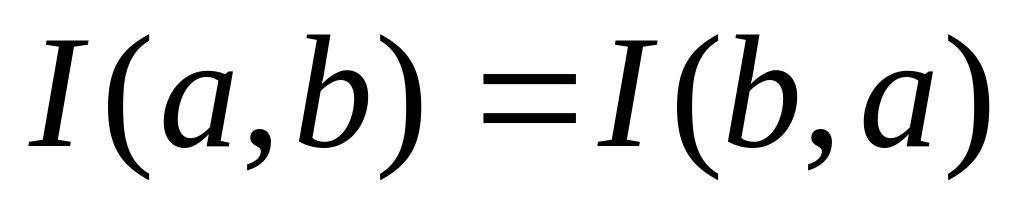
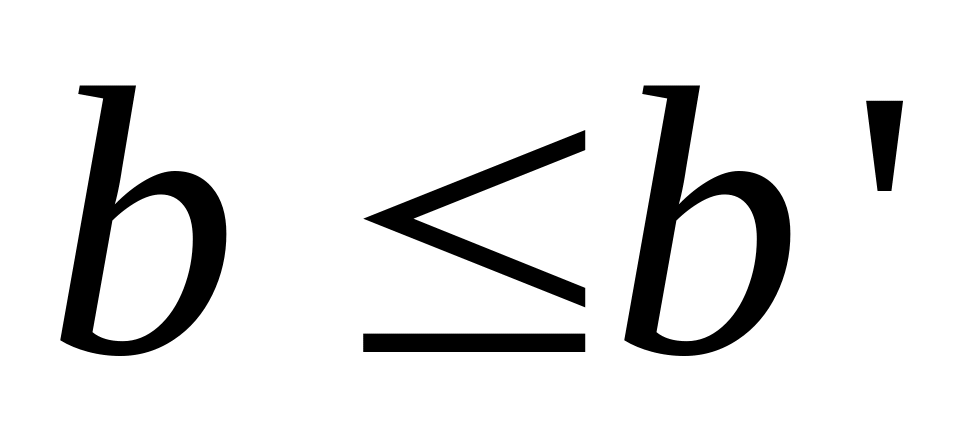3. Монотонность: если и , то I (a,b) I (a’,b’)

4. Ассоциативность: I (I (a,b),c)= I (a, I (b,c))

5. I – непрерывная функция

6. Идемпотентность: I (a, a)= a

В качестве примеров операции нечеткого пересечения можно использовать(я бы не стал писать это):

1) Стандартное нечеткое пересечение, т.е.

2) Так же можно рассмотреть нечеткое пересечение Ягера:

,

Очевидно что при w=1 операция пересечения будет представлять собой:

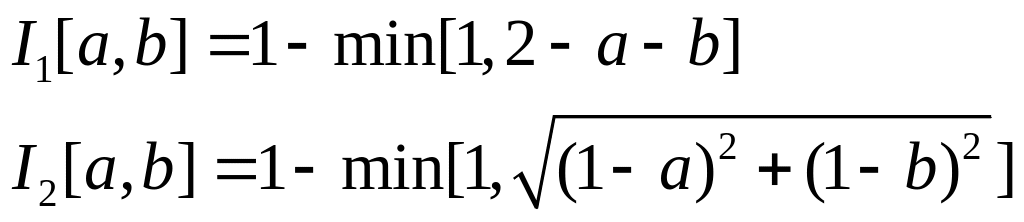
И при – – стандартная операция пересечения.

{Нечеткое пересечение удовлетворяет аксиомам 1-5, но не удовл. 6}

3) Алгебраическое (вероятностное) произведение:

Здесь выполняются свойства коммутативности, ассоциативности, тождественности и законы де Моргана.

4) Граничное произведение:

Данная операция идентична операции нечеткого пересечения Ягера при w=1.

Для этой операции выполняются свойства коммутативности, ассоциативности, тождественности, законы де Моргана и не выполняются свойства идемпотентности и дистрибудивности.

5) Драстическое(сильное) произведение

6) Произведение Хамахера.

7) Лямбда-сумма.