14. Понятие нечеткой переменной, понятие лингвистической переменной, логико-лингвистическая шкала.

Нечеткая переменная характеризуется тройкой < ,Х,A>, где

– наименование переменной,

Х – универсальное множество,

A – это нечеткое множество, заданное на универсальном множестве Х с использованием функции принадлежности .

Понятие лингвистической переменной.

Значениями лингвистической переменной являются нечеткие переменные.

Лингвистическая переменная характеризуется пятью параметрами:

Здесь B – наименование лингвистической переменной,

T – множество значений лингвистической переменной, представляющие собой наименования нечетких переменных каждая из которых задана на универсальном множестве Х,

G – синтаксическая процедура, позволяющая оперировать элементами Т, и в частности генерировать новые значения, для данного множества.

М – семантическая процедура, позволяющая превратить каждое новое значение нечеткой переменной, которая сгенерирована синтаксической процедурой G. Лингвистические переменные могут быть составными.

Пример:

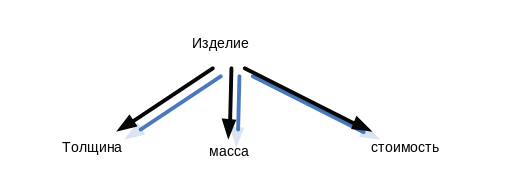
Пусть у нас задана лингвистическая переменная B – толщина изделия(наименование), и задана терм-множеством

Т={«малая», «средняя»,«большая»}

Х=[10,80]

Логико-лингвистическая шкала.

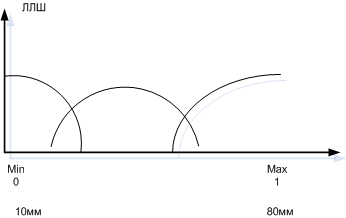
Хорошо бы что бы пересечение проходило выше уровня 0.5, либо меньше 0.5.

Построение ЛЛШ это первый (подготовительный) этап, перед работой с нечеткими переменными.

15. Области применения нечетких моделей. Классификация нечетких моделей.

Области применения нечеткого моделирования.

1. Недостаточные или неопределенные знания об объекте системы.

Иногда получение информации о системе сложный или дорогостоящий процесс. Выделить систему из среды не всегда удается.

2. Адекватная обработка неопределенной информации.

Существуют разного рода типы неопределенностей:

1. Стохастическая неопределенность (присуща для случайных объектов)

2. Нестохастическая неопределенность. Накладывается ряд различных фактов – нечеткие модели.

1. «Прозрачное моделирование» и идентификация.

Классификация нечетких моделей.

В зависимости от назначения, положения теории нечеткой логики и нечетких множеств могут быть использованы:

1. Непосредственно при описании системы.

   1. Нечеткие продукционные модели.

   2. Нечеткие функциональные модели.

   3. Нечеткие реляционные модели

2. При задании нечетких параметров системы. 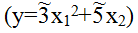-нечеткие числа.

3. При задании входов и выходов и состояний системы на основе нечетких множеств.

4. Нечеткие модели с использованием нескольких ранее описанных.

16. Определение нечеткой продукционной модели. Компоненты нечетких продукционных моделей.

Нечеткие продукционные модели (НПМ) являются наиболее используемыми при описании плохо структурированных процессов и систем.

НПМ – согласованное множество отдельных нечетких продукционных правил вида: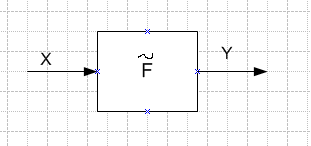

Если x есть А, то y есть В

предназначенных для определения степени истинности заключения правил на основе предпосылок с известной степенью истинности.

Если x есть А – предпосылка (антецедент)

y есть В – заключение (консеквент)

A и В – некоторые нечеткие множества; х, у – переменные.

Для того, чтобы построить НМ, необходимо задать следующее ее компоненты:

1. Способ нечеткого вывода

2. База нечетких продукционных правил

3. Процедура введения нечеткости (фазификации - fuzzification)

4. Процедура агрегирования степени истинности предпосылок по каждому из нечетких продукционных правил (aggregation)

5. Процедура активизации заключений каждого из нечетких правил (activation)

6. Процедура аккумулирования активизированных заключений всех правил для каждой выходной переменной (accumulation)

7. Приведение к четкости выходной переменной (defuzzification)

8. Процедура параметрической оптимизации конечной базы нечетких продукционных правил

Прямой способ нечеткого вывода: правило «нечеткий модус поненс», этапы способа

Этап 1. Задается нечеткая импликация – это нечеткое причинно-следственное отношение между предпосылкой А и заключением В.

R: A->B

Если х есть А, то у есть В.

x – нечеткая входная переменная

(Х – область определения предпосылок нечеткого правила)

y – выходная нечеткая переменная ( )

А – нечеткое множество, определенное на Х с функцией принадлежности

B – нечеткое множество, определенное на У с функцией принадлежности .

Этап 2. Задание нечеткого условия или факта.

«x’ есть А’»

х’ – фактическое значение переменной х,

А’ – нечеткое множество, отражающее значение х’, определенное на множестве Х с функцией принадлежности .

Этап 3. Формирование вывода.

«y’ есть B’», где

y’ – полученное значение переменной,

B’ – нечеткое множество, отражающее значение y’, определенное на множестве Y с функцией принадлежности .

Нечеткое условие из этапа 2 содержит нечеткое множество A’, которое является «близким» в определенном смысле к нечеткому множеству А, в результате формируется вывод в виде функции принадлежности нечеткого множества B’, характеризующее степень его близости к нечеткому множеству B.

Процесс получения результата прямого нечеткого вывода B’ с использованием нечеткой импликации A->B и нечеткого условия «x’ есть А’» можно представить в виде:

Нечеткая импликация A->B соответствует нечеткому отношению R, которое может рассматривать как нечеткое подмножестводекартова произведения полного множества предпосылок х и заключений y. Функция принадлежности отношения R: .

В результате функцию пренадлежности нечеткого множества B’ можно представить в следующем виде: