Лабораторная работа № 4 Измерение активной мощности и энергии в трехфазной трехпроводной сети

Цель работы:

1. Ознакомление с методами и приборами для измерения активной мощности и энергии.

2. Определение коэффициента мощности в трехфазных трехпроводных сетях низкого напряжения.

Основные теоретические положения

1. Измерение активной мощности.

Для измерения активной мощности трехфазной системы применяют различные схемы включения ваттметров.

При симметричной нагрузке активную мощность цепи можно измерить одним ваттметром, включенным в одну из фаз приемника (W₆ , рис.8):

Р = 3Р_ф = 3U_ф I_ф cos _ф = U_лI_л cos _ф .

При несимметричной нагрузке, соединенной звездой, в трехфазной четырехпроводной цепи мощность можно измерить тремя ваттметрами, включенными в каждую из фаз:

Р = Р_А + Р_В + Р_С .

Измерение активной мощности в трехфазной трехпроводной сети, независимо от способа соединения нагрузки и симметрии системы, может быть осуществлено с помощью двух однофазных ваттметров, включенных по схеме двух приборов. Одна из возможных схем включения показана на рис.1.

Активная мощность трехфазной цепи при данном включении равна алгебраической сумме показаний двух ваттметров:

Так как = 0 ,

то ; ;

Р = Re( + + ) = Re[( ) +( ) ] =

= Re{ + } = U_ABI_Acos( ) + U_CBI_C cos( ).

36

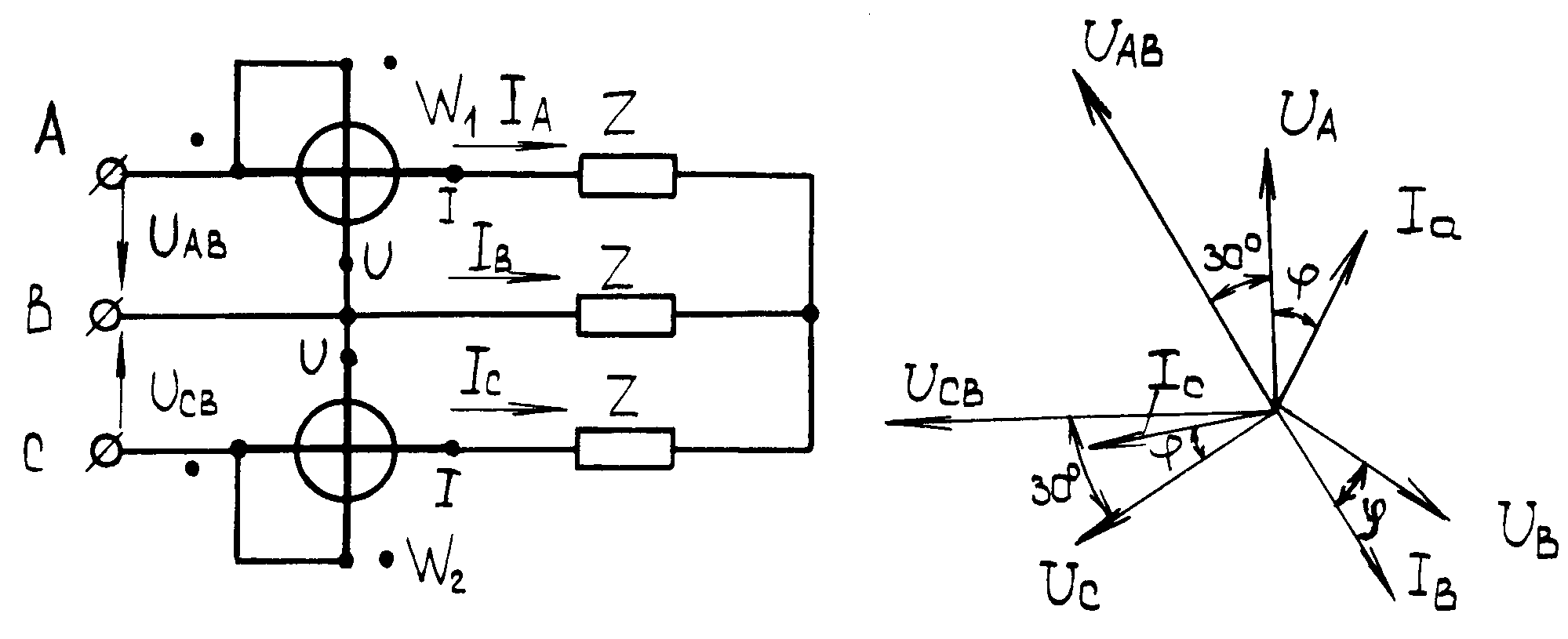
Рис.1 Рис.2

Векторная диаграмма для данной схемы в случае симметричной нагрузки приведена на рис.2.

При симметричном приемнике

Р = U_лI_л[cos (30+ ) + cos (30- )] . (2)

Из уравнения (2) видно, что при  = 0 (активная нагрузка) оба ваттметра будут иметь одинаковые показания, при  = 60 показание первого ваттметра становится равным нулю, а при   60 показание этого ваттметра становится отрицательным. В последнем случае для нахождения полной активной мощности необходимо взять не сумму, а разность показаний обоих ваттметров.

Кроме однофазных ваттметров при определении активной мощности в трехфазной трехпроводной сети промышленного назначения применяются ферродинамические двухэлементные киловаттметры (рис.3)

Конструктивно (рис.4) каждый из элементов состоит из неподвижной обмотки (НО), включенной последовательно в один из проводов токовой цепи (И₁ , И₂), и подвижной рамки (ПР), включаемой на соответствующее напряжение.

Каждый элемент механизма имеет собственный магнитопровод с равномерным магнитным полем в воздушном зазоре. Подвижные рамки закреплены на одной оси и находятся в одной плоскости.

Оба элемента включаются в трехфазную трехпроводную сеть по схеме двух приборов для измерения активной мощности.

37

На подвижную часть киловаттметра действует алгебраическая сумма вращающих моментов обоих элементов и показания прибора пропорциональны полной мощности в соответствии с формулой (1).

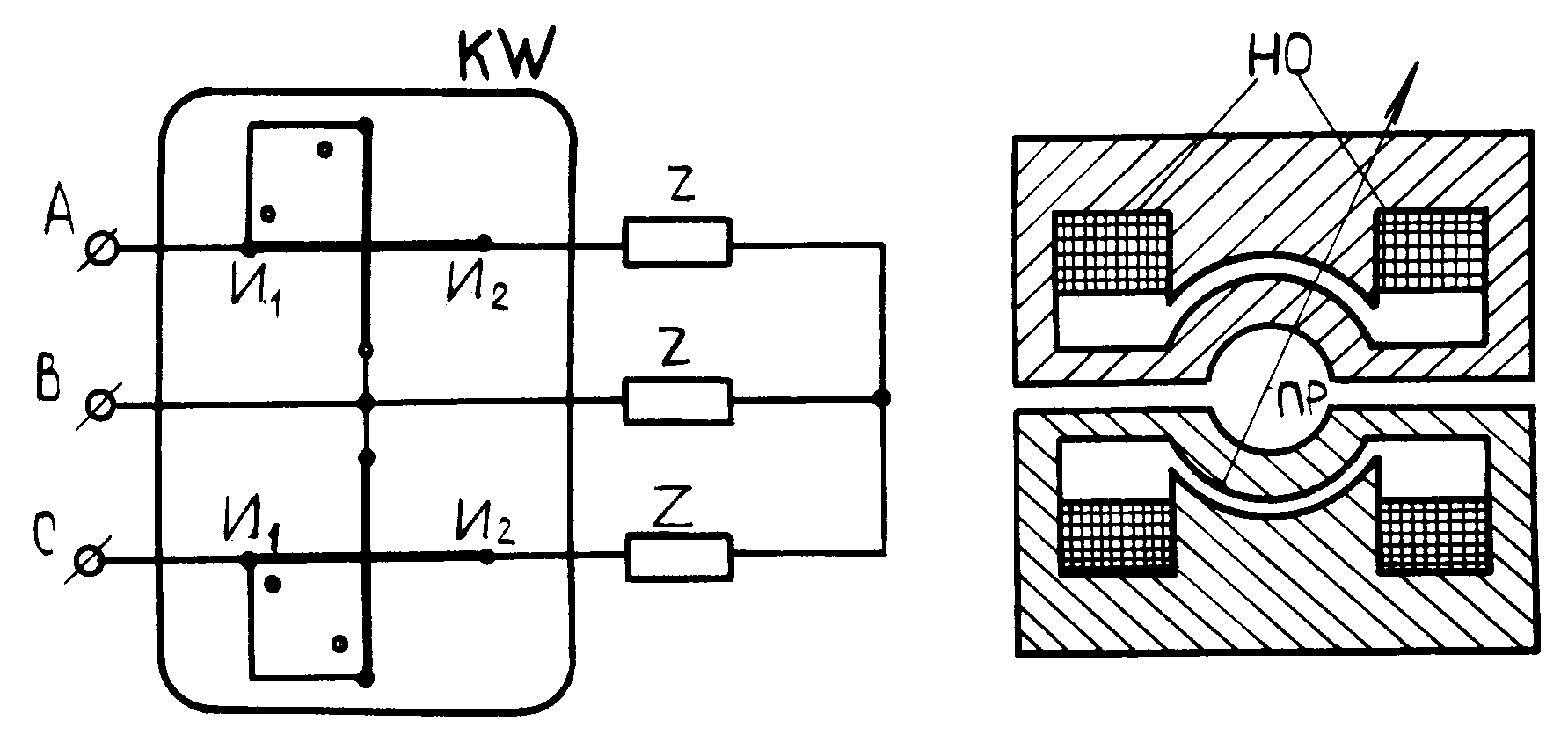
Рис.3 Рис.4

2. Измерение энергии.

Измерение энергии в трехфазной сети осуществляется с помощью индукционных приборов (счетчиков). Устройство индукционного счетчика показано на рис. 5.

Подвижной частью счетчика служит алюминиевый диск 1, укрепленный на оси 2 и расположенный в воздушном зазоре между двумя электромагнитами. На стержне электромагнита напряжения расположена катушка с большим числом витков тонкого провода, ток которой I_U создает магнитный поток Ф, состоящий из двух потоков Ф_U и Ф_L. Рабочий поток Ф_U пересекает диск и замыкается через противополюс 3. Шунтирующие потоки Ф_L не пересекают диска, замыкаясь по боковым стержням электромагнита. Токовый электромагнит выполнен с большим воздушным участком в магнитной цепи, а по его катушке с малым числом толстого провода проходит ток потребителя I , создающий магнитный поток Ф_I. Рабочий поток Ф_I дважды пересекает диск.

Таким образом, диск пересекают три не совпадающие в пространстве и сдвинутые по фазе потока. Взаимодействие этих потоков с токами, индуктированными ими в диске, приводит к возникновению вращающего момента:

M = K₁Ф_UФ_I sin  , (4)

где  - угол сдвига фаз между рабочими потоками Ф_U и Ф_I .

38

Так как магнитный поток Ф_U пропорционален напряжению, а Ф_I - току, то для того, чтобы счетчик реагировал на энергию, необходимо выполнить условие

sin  = cos  , (5)

где  - угол сдвига фаз между напряжением U и током I.

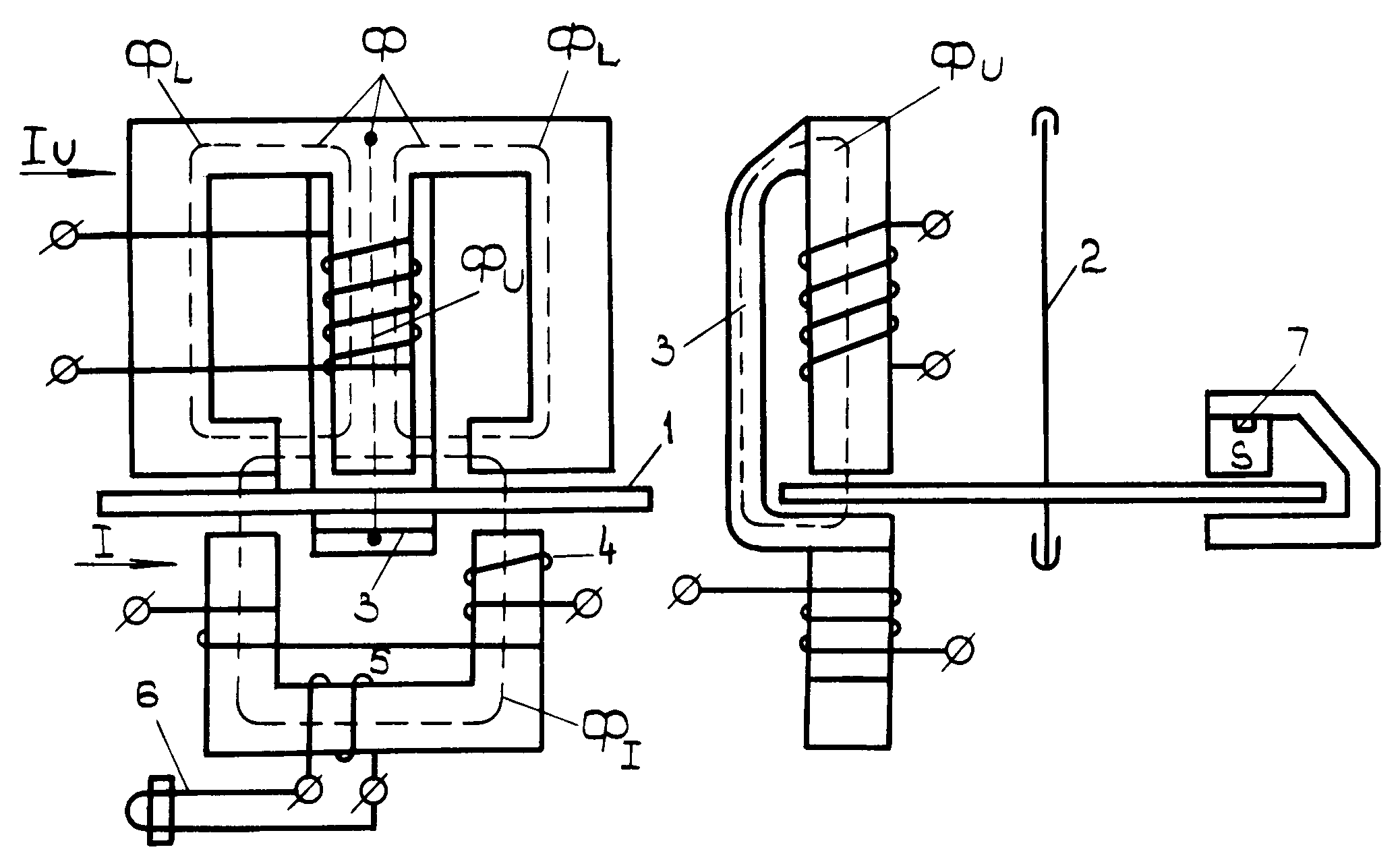
Рис.5

В этом случае

M = K₂UI cos  = K₂P , (6)

то есть вращающий момент пропорционален активной мощности нагрузки. Противодействующий элемент создается тормозным магнитом и пропорционален скорости вращения диска:

М_т = K₃ . (7)

В установившемся режиме М = М_т диск вращается с постоянной скоростью. Приравняв выражения (6) и (7) и решая полученное уравнение, найдем K₂ = K₃ ,

39

где = W - энергия, прошедшая через счетчик за время t ;

= 2N ,

где N – число оборотов диска за время t ;

откуда

W = = C_нN , (8)

где C_н - постоянная счетчика, то есть энергия, регистрируемая счетчиком за один оборот.

Для учета числа оборотов диска служит счетный механизм. Передаточное число счетного механизма определяет соотношение между единицей энергии, регистрируемой счетчиком, и числом оборотов диска. Передаточное число счетчика указывается на его щитке:

1кВт/ч = N₀ оборотов диска.

Тогда постоянная счетчика С_н будет равна:

С_н = . (9)

Чтобы выяснить, каким образом обеспечивается выполнение условия (5), построим векторную диаграмму счетчика (рис.6).

Из векторной диаграммы видно, что угол  между потоками Ф_U и Ф_I равен:  =  - _I - . Для выполнения условия (5) необходимо, чтобы  - _I = 90 или  = 90 + _I . Тогда

M = К₂UIcos  = K₂P .

Выполнение условия   90 обеспечивается наличием большого нерабочего потока Ф_L (Ф_L Ф_U). Обеспечение равенства  - _I = 90 осуществляется изменением угла потерь _I с помощью короткозамкнутых витков 4 и обмотки 5 с регулируемым сопротивлением 6.

Для создания тормозного момента и обеспечения равномерной скорости вращения диска при каждой нагрузке служит постоянный магнит 7. Схема включения индукционного счетчика показана на рис.7.

40

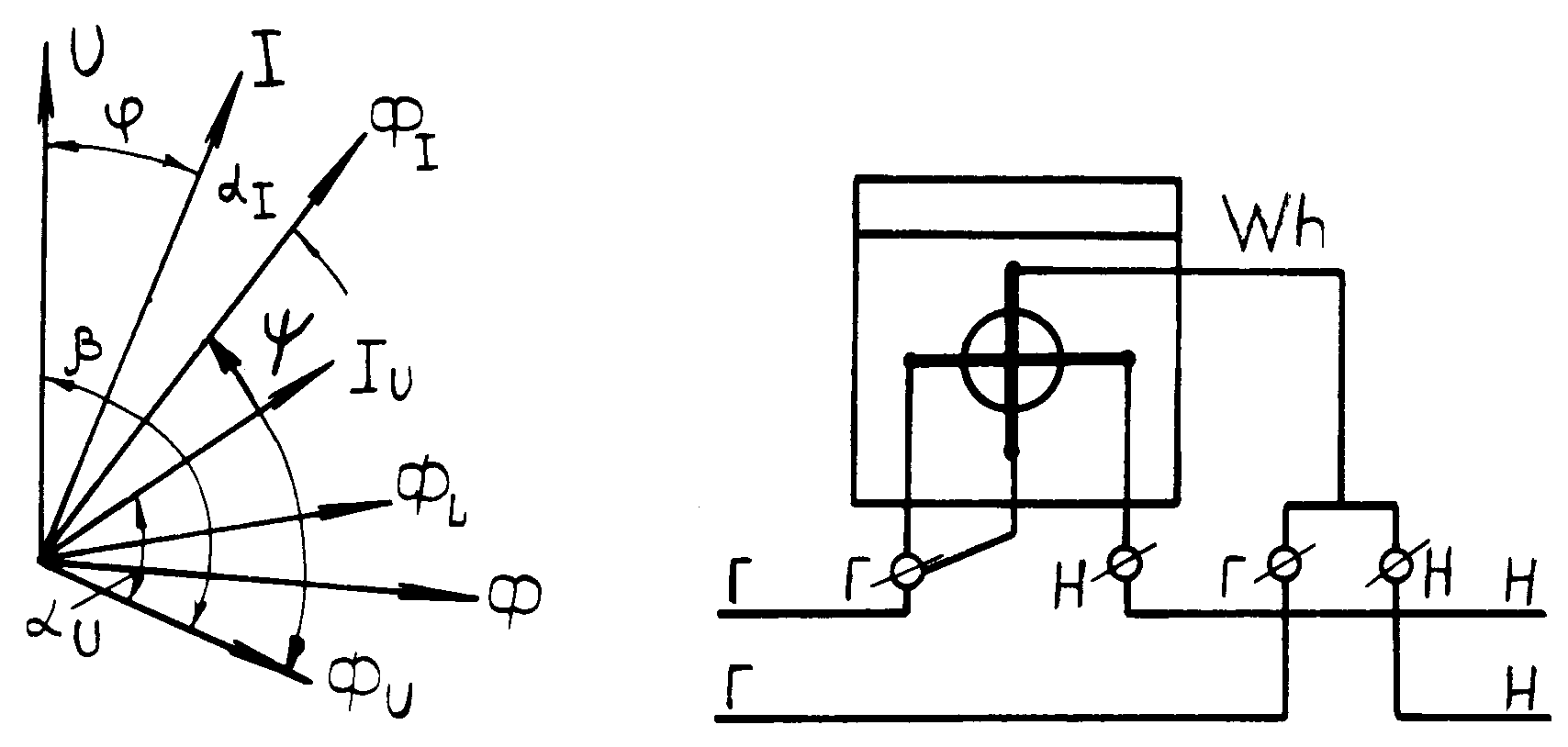
Рис.6 Рис.7

3. Измерение коэффициента мощности

Измерение cos  производится косвенным методом. При симметричной нагрузке напряжения и токи в фазах равны, поэтому необходимо измерить напряжение U_ф на нагрузке Z_н и проходящий по ней ток I_ф в какой-либо фазе. Методом одного ваттметра следует измерить активную мощность в этой фазе и по формуле cos  = найти коэффициент мощности.

Порядок выполнения работы

1. Ознакомиться с лабораторным стендом. Записать паспортные данные всех приборов.

2. Собрать схему, показанную на рис.8.

Рис.8

41

3. В качестве потребителя Z_н подключить:

а) активную нагрузку (рис.9);

б) активно-индуктивную нагрузку с последовательным включением потребителей (рис.10);

в) активно-индуктивную нагрузку с параллельным включением потребителей (рис.11).

4. Для каждого вида нагрузки определить мощность всей трехфазной цепи и в фазе В – активную и полную. Определить активную энергию за время, составляющее не менее 60 с. Для этого нужно определить число оборотов диска каждого счетчика за 60 с, вычислить номинальную постоянную счетчика по формуле (9), затем определить потребляемую энергию за секунду по формуле (8). Показания приборов занести в таблицу.

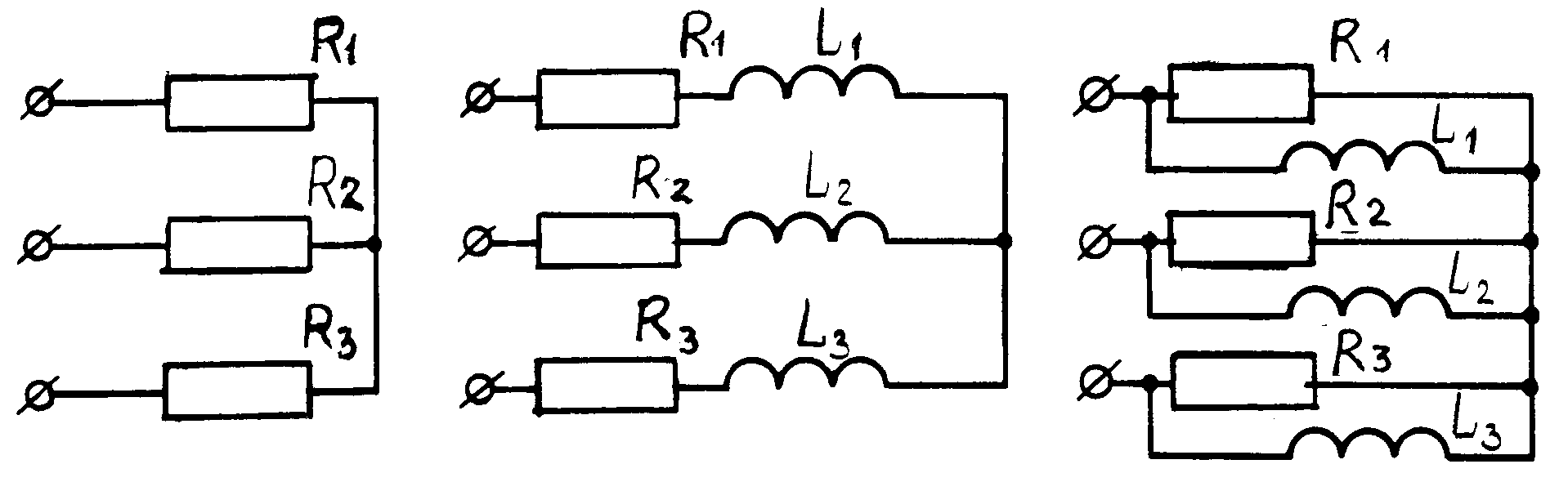
Рис.9 Рис.10 Рис.11

Ваттметры W₁ и W₂ соединены по схеме двух приборов, и сумма их показаний дает мощность трехфазной цепи, равную:

P = P₁ + P₂ .

Счетчики включены также по схеме двух приборов, и сумма их показаний дает энергию, потребляемую трехфазной нагрузкой:

W = W₄ + W₅ .

Таблица

Измерено

Вычислено

P1, Вт

P2, Вт

P3, Вт

W4, Вт·с

W5, Вт·с

P6, Вт

Iф, А

Uф В

P, Вт

W, Вт·с

cos



R

R-L послед.

R-L паралл.

42

Угол сдвига фаз между током и напряжением на нагрузке равен:

 = arccos = arccos .

В данной работе активная мощность трехфазной симметричной нагрузки измеряется различными способами. При этом

P = P₁ + P₂ = P₃ = P₄ + P₅ = 3P₆ .

Вопросы для самоконтроля

1. Доказать, что полная активная мощность трехфазной цепи равна алгебраической сумме показаний обоих ваттметров.

2. Как изменяются показания ваттметра в зависимости от характера нагрузки? Показать на векторной диаграмме.

3. В каких случаях мощность трехфазной цепи может быть измерена одним ваттметром? Привести схемы подключения ваттметра при соединении нагрузки звездой и треугольником в трехпроводной трехфазной цепи.

4. Какие приборы применяются для измерения активной мощности в трехфазных цепях? Рассказать их устройство и принцип действия.

5. Какие приборы применяются для измерения активной энергии в трехфазных цепях? Привести схемы включения приборов.

6. Рассказать устройство и принцип действия однофазного индукционного счетчика.

7. Чему равен вращающий и тормозной моменты индукционного механизма?

8. Что такое передаточное число и постоянная счетчика?

9. Что нужно выполнить для того, чтобы вращающий момент счетчика был пропорционален активной мощности? Каким образом обеспечивается выполнение этого условия? Пояснить на векторной диаграмме.

10. Как определяется угол  между током и напряжением на нагрузке?

Список литературы

1. Электротехника / Под ред. В. Г. Герасимова. – М.: Высшая школа, 1986. – С. 272-286, 304-310.

2. Иванов А. Электротехника: Лабораторные работы. – Киев: Вища школа, 1976. – С. 130-136.

43

Лабораторная работа № 5

Исследование резонансных явлений в разветвленной

электрической цепи синусоидального тока

Цель работы:

1. Исследовать электрическое состояние линейной разветвленной цепи синусоидального тока при различных параметрах цепи.

2. Экспериментально проверить условие, при котором наблюдается резонанс токов. Определить добротность цепи.

3. Вычислить коэффициент мощности. При различных параметрах цепи определить активную, полную и реактивную мощности.

4. Построить по опытным данным векторные диаграммы напряжения и токов при различных режимах цепи: до резонанса, при резонансе и после резонанса.

Основные теоретические положения

Если к зажимам электрической цепи (рис.1), состоящей из параллельно соединенных катушки индуктивности (с активным сопротивлением R_к и индуктивностью L) и батареи конденсаторов (емкостью С), приложено напряжение, меняющееся во времени по синусоидальному закону u (t) = U_m sin t , то токи в параллельных ветвях и неразветвленной части цепи также будут синусоидальными:

i_к (t) = sin (t - _к) = I_mк sin (t - _к) ;

i_с (t) = sin (t + _c) = I_mc sin (t + _c) ;

i (t) = i _к(t) + i _с(t) ,

где X_с = - сопротивление батареи конденсаторов;

X_к = L_к - индуктивное сопротивление катушки;

Z_к = - полное сопротивление катушки индуктивности;

; ;  = 2f ;

f – частота синусоидального тока.

44

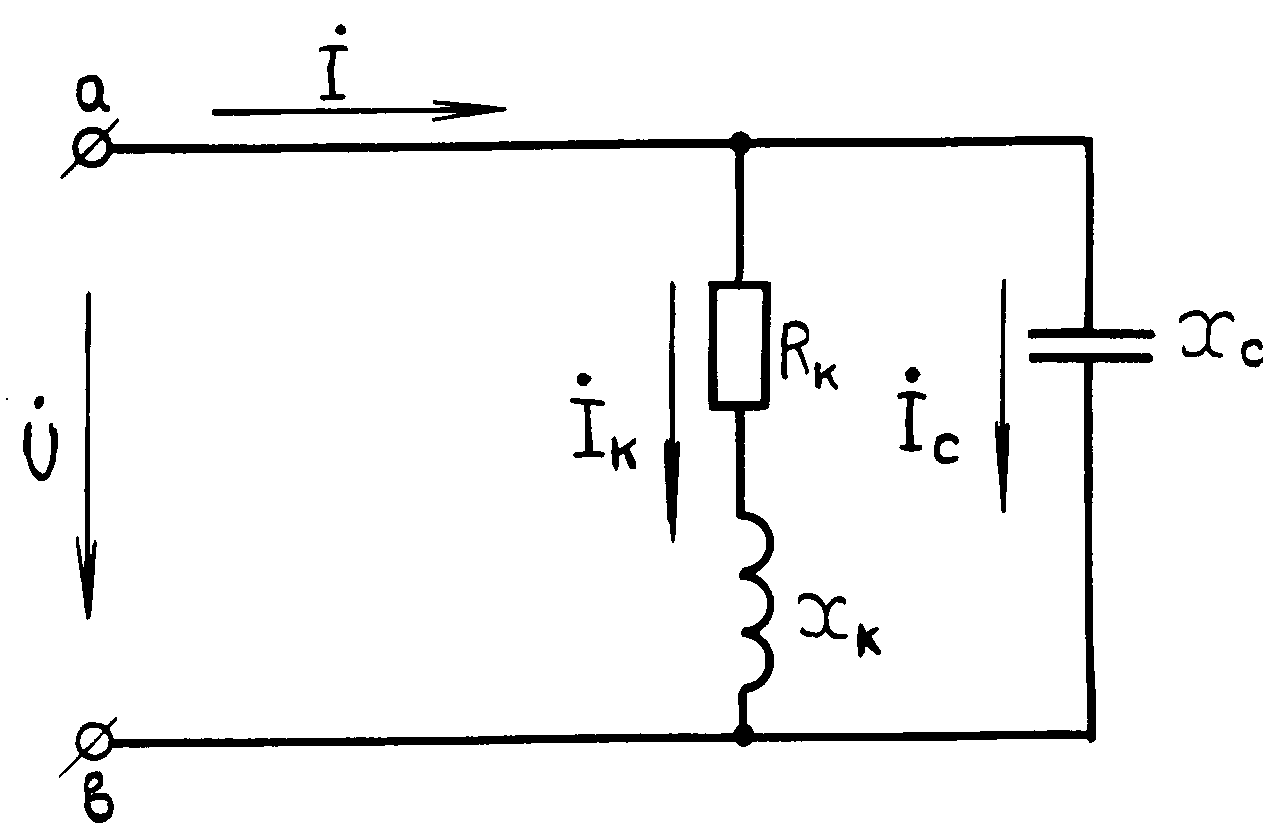
Рис. 1

По закону Ома в комплексной форме ток в катушке равен:

= = = =

= (g_к – j b_к) = Y_к = ,

где Y_к = g_к – j b_к - комплекс полной проводимости катушки;

- активная проводимость катушки;

- индуктивная проводимость катушки;

g_к - активная составляющая тока катушки, совпадающая по фазе с напряжением ;

– j b_к - реактивная составляющая тока катушки, отстающая по фазе от напряжения на  /2.

Ток в ветви с конденсатором равен: = = jС = jb_c .

Ток в неразветвленной части цепи определяется формулой

=

или = [g_к – j(b_к – b_c)] = Y ,

где Y = g_к – j (b_к – b_c) = ye^-j = y cos  + jy sin  - комплекс полной проводимости всей цепи (рис.1);

45

 = arctg - угол между напряжением U, приложенным ко всей цепи, и током в неразветвленной части цепи I;

y = - модуль полной проводимости цепи;

Векторная диаграмма токов (рис.2) строится на основании уравнения, составленного по первому закону Кирхгофа. Начальную фазу напряжения принимают равной нулю, то есть = U, вектор напряжения совмещается с осью +I на комплексной плоскости.

На рис.2 приведена векторная диаграмма для случая, когда b_c  b_к (после резонанса) и напряжение отстает по фазе от тока на угол    /2. Ток в неразветвленной части цепи носит активно-емкостной характер ( I_c  I_кр).

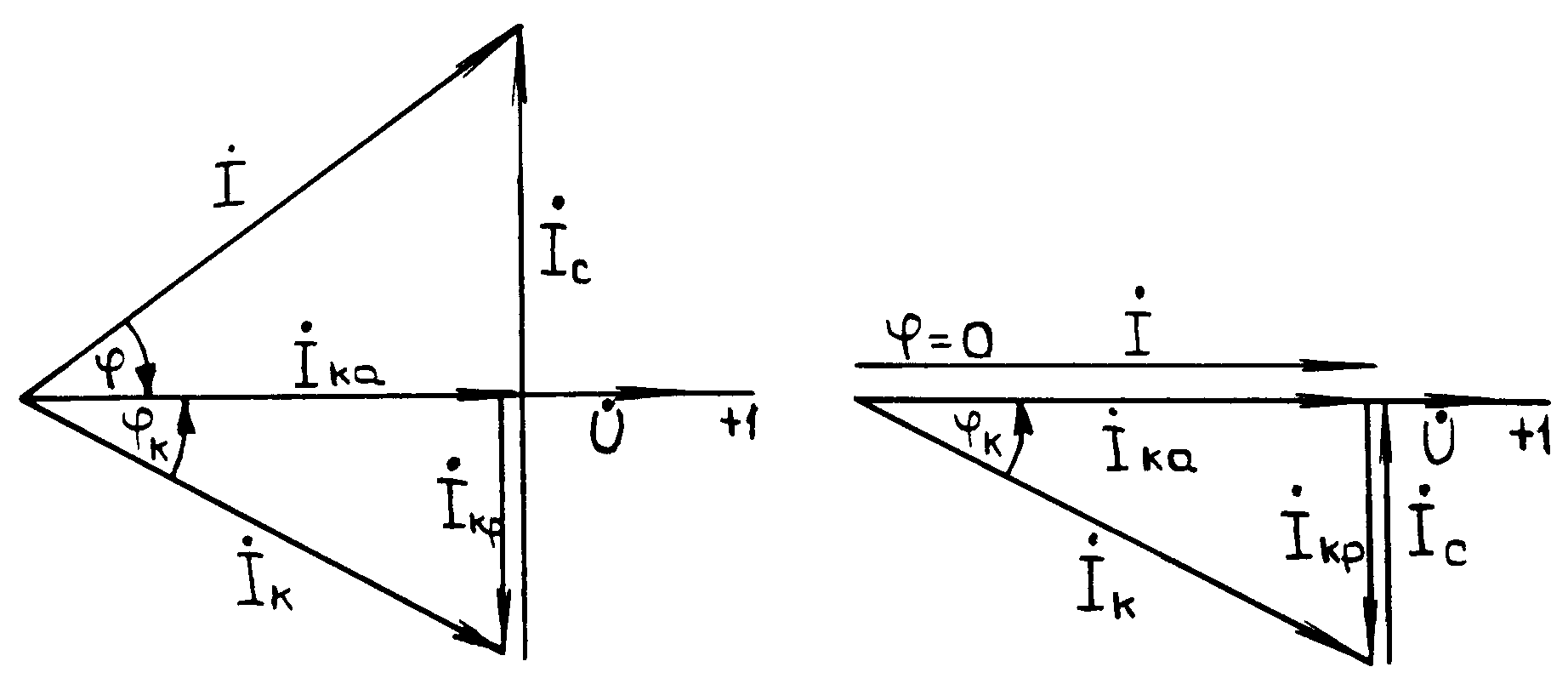
Рис.2 Рис.3

Резонансом тока называют явление в параллельной цепи с емкостными и индуктивными приемниками, когда общий ток в неразветвленной части цепи и напряжение на входе цепи совпадают по фазе. Резонанс токов характеризуется равенством реактивных токов в индуктивном и емкостном приемниках. Ток в неразветвленной части цепи минимальный, совпадает по фазе с напряжением и определяется активными составляющими токов емкостного и индуктивного приемников. Для цепи, представленной на рис.1, резонансное состояние характеризуется соотношениями:

, ,  = 0 .

Векторная диаграмма для резонансного режима представлена на рис.3.

46

Ток в неразветвленной части цепи определяется выражением

I = y U = U .

Поскольку при резонансе ток в неразветвленной части цепи чисто активный, то условием резонанса является равенство реактивных проводимостей приемников:

b_к = b_с или + ₀² L_к² = ₀C .

Это условие называется условием резонанса токов. Резонансное состояние можно получить, изменяя параметры цепи С, L_к , R_к или частоту напряжения сети .

Резонансная частота f₀ = ₀ / 2 определяется из условия резонанса

f₀ = .

Видно, что резонанс возможен лишь при условии R_к . При резонансе ток в цепи I минимален : I = gU.

Реактивные токи в приемниках могут оказаться больше активного тока в неразветвленной части цепи. Превышение реактивных токов приемников при резонансе по сравнению с активным током в неразветвленной части цепи характеризуют добротностью цепи q.

q = .

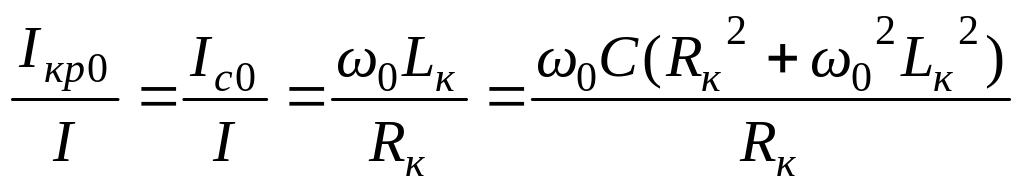Мгновенная мощность в цепи есть произведение мгновенных значений тока и напряжения р(t) = u(t) i(t) .

Активная мощность – среднее за период значение мгновенной мощности, то есть активная мощность характеризует среднюю мощность преобразования энергии в цепи в другие виды энергии:

P = UI cos  .

При параллельном соединении

P = UI_a = U²g ,

где U и I – соответственно действующие значения напряжения и тока в цепи;

47

 - угол сдвига по фазе между током и напряжением в цепи, зависит от характера нагрузки; g - активная проводимость цепи.

Полная мощность цепи – мощность, подводимая к зажимам цепи и характеризующая амплитуду колебаний мощности в цепи. Определяют полную мощность произведением действующих значений тока и напряжения

S = UI .

Реактивная мощность цепи – мощность, периодически запасаемая в реактивных элементах и отдаваемая ими обратно генератору, равная:

Q = UI sin  .

Комплексная форма полной мощности

= Scos  + jS sin  = P + jQ

дает возможность построить векторную диаграмму мощностей – треугольник мощностей (рис.4). Из векторной диаграммы мощностей находим полную мощность: S =

При резонансе реактивная мощность цепи Q = 0. Реактивные мощности на участках цепи с L_к и C характеризуют взаимное преобразование энергии электрического и магнитного полей индуктивности и емкости. Активная мощность P = S.

Р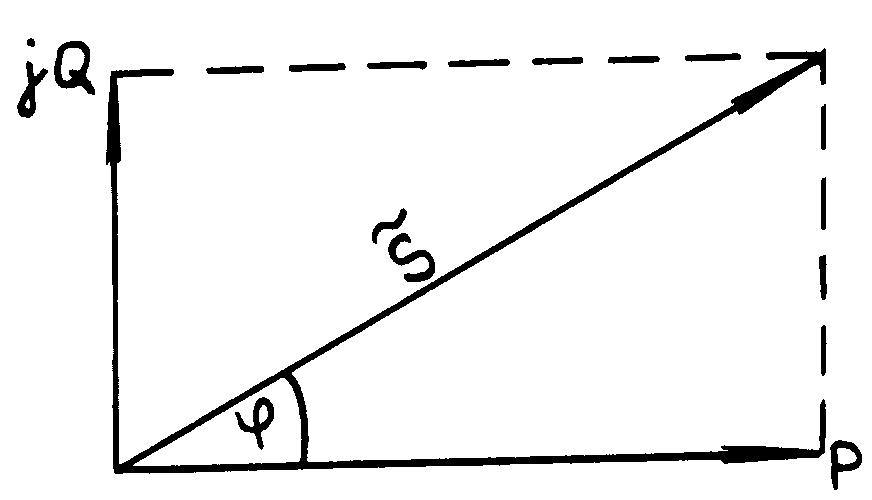 езонанс токов используют в установках для повышения коэффициента мощности, подключая параллельно приемнику с сосредоточенными параметрами R, L конденсаторную батарею емкостью С:

C = I_c / 2fU = I_к sin _к / 2fU ,

Рис.4

которая обеспечивает полную компенсацию сдвига фаз между напряжением U и током I, при этом коэффициент мощности cos  = 1 и источник электрической энергии полностью разгружается от реактивного тока (S = P). Обычно коэффициент мощности установок доводят до 0,9…0,95. Еще большее повышение cos  требует больших затрат на установку батарей конденсаторов, которые экономически не оправдываются. В этом случае емкость батареи конденсаторов определяется формулой

C = (P / 2fU ²)(tg _н - tg ) ,

где P - активная мощность приемника;

_н - угол сдвига по фазе приемника;

 - требуемый угол сдвига по фазе.

48

Повышение коэффициента мощности установок снижает ток в линии электропередач, потери в линии P_л = I²R_л .

Описание установки

Экспериментальное исследование линейной разветвленной электрической цепи синусоидального тока выполняют на установке, схема которой приведена на рис.5. Цепь состоит из параллельно соединенных индуктивной катушки и конденсаторной батареи переменной емкости. Питание установки осуществляется от сети переменного тока 0 - А через двухполюсный выключатель В и регулирующий автотрансформатор ЛАТР, которым поддерживают на зажимах приемников заданную величину напряжения U, измеряемую вольтметром V. Ваттметр W измеряет активную мощность в цепи, а амперметры А, А₁, А₂ – токи I, I₁ , I₂ соответственно в неразветвленной части цепи и в отдельных ветвях.

Рис.5

Порядок выполнения работы

1. Ознакомиться с приборами и оборудованием экспериментальной установки и записать технические характеристики в отчет.

2. Собрать схему, показанную на рис.5.

3. Поставить ручки регулирующего автотрансформатора ЛАТР в нулевое положение, выключить все конденсаторы в батарее и после проверки схемы руководителем замкнуть двухполюсный выключатель В.

4. Установить поворотом ручки регулирующего автотрансформатора заданную преподавателем величину напряжения U (80…100 В) на входе электрической цепи и на протяжении всего опыта поддерживать ее неизменной.

49

5. Изменяя емкость батареи конденсаторов, добиться резонанса в цепи: ток в неразветвленной части цепи достигнет минимального значения, активная мощность P = UI. Зафиксировать резонансную емкость.

6. Произвести опыты, изменяя емкость от 0 до C_p (3…5 опытов) и в таких же пределах выше C_p. Вблизи резонансной емкости измерения делать чаще. Данные измерений занести в табл. 1.

7. Результаты вычислений занести в табл. 1, 2. Учитывая, что параметры катушки индуктивности не изменялись, их достаточно вычислить один раз, например при резонансной емкости. При резонансе определить добротность цепи q.

8. По данным табл. 1 построить кривые I_c(C), I_к(C), I(C), cos  =f (C),  = f (C).

9. По опытным данным в масштабе построить три векторные диаграммы: до резонанса, в момент резонанса, после резонанса.

Указание: При построении векторной диаграммы нужно вспомнить, что I_к=I_L , только тогда, когда R_к  0.

В нашем опыте R_к  0, поэтому , где I_ка и I_кр – активная и реактивная составляющие тока катушки; I_ка = g_кU; I_кр = b_кU или (см. рис.2): I_ка =I_к cos _к ; I_кр = I_к sin _к = ; cos _к = .

Так как активная мощность выделяется только на катушке, то показание ваттметра P и есть мощность катушки P_к.

Отсюда P = P_к = UI cos  = UI_к cos _к = UI_ка = g_кU² = R_кI _к ² .

Построение векторной диаграммы токов и напряжений можно проводить так (рис.2):

1. Совместить вектор с действительной осью;

2. Под углом _к отложить вектор = I_к e^{-jк ;}

3. От вектора провести вектор , опережающий напряжение на угол /2;

4. Замыкающий вектор = + .

При изменении емкости параметры катушки не изменяются, поэтому не изменяется ни величина, ни направление вектора , изменяется лишь по величине вектор .

Для исследуемой катушки известно: U, I_к , P_к= P.

50

По этим данным рассчитываются параметры катушки:

Z_к = U/ I_к , R_к = P/ I _к² , X_к = , L_к = X_к/ 2f , f = 50 Гц.

Для конденсатора известно U, I_c . Отсюда X_c = U/ I_c , b_c = I_c / U.

Таблица 1

№ Данные наблюдений

Результаты вычислений

С, мкФ

U, В

I, А

Iс , А

Iк , А

P, Вт

S, ВА

Q , ВАр

cos

y, См1

qк , Ом1

bк , Ом1

bc , Ом1

xc , Ом

q

19

100

Таблица 2

C = Cp мкФ	Результаты вычислений
	Zк	Rк	Xк	cos к	Lк	gк

Вопросы для самоконтроля

1. Как определить полное сопротивление ветви электрической цепи синусоидального тока?

2. Какие величины определяют знак реактивного сопротивления ветви той же электрической цепи?

3. Как рассчитать ток в неразветвленной части электрической цепи синусоидального тока?

4. В какой электрической цепи и при каких условиях может возникнуть резонанс токов?

5. Чему равен коэффициент мощности цепи при резонансе токов?

6. Могут ли действующие токи в ветвях электрической цепи превышать действующий ток в неразветвленной части этой же цепи?

7. Какими величинами нужно располагать для расчета емкости конденсаторной батареи, обеспечивающей повышение коэффициента мощности установки до данного значения? До какого значения целесообразно повышать коэффициент мощности установок?

8. Чему равна реактивная мощность в цепи при резонансе токов?

Список литературы

1. Электротехника / Под ред. В. Г. Герасимова. – М.: Высшая школа, 1985. – С. 73-78, 81-88.

2. Касаткин А. С., Немцов М. В. Электротехника. – М.: Энергоатомиздат, 1983. – С. 63-98.

3. Иванов А. А. Электротехника: Лабораторные работы.- Киев: Вища школа, 1976. – С. 60-67.

51

Лабораторная работа № 6

Исследование резонансных явлений в неразветвленной

электрической цепи синусоидального тока

Цель работы:

1. Исследовать электрическое состояние линейной неразветвленной цепи синусоидального тока при различных приемниках.

2. Экспериментально проверить условие, при котором наблюдается резонанс напряжений. Определить добротность цепи.

3. По опытным данным построить векторные диаграммы напряжений и тока. Рассчитать параметры отдельных элементов электрической цепи.

Основные теоретические положения

При расчете неразветвленной электрической цепи синусоидального тока с последовательно соединенными приемниками, например катушкой индуктивности и конденсатором, характеризуемых параметрами R_к , L и С (рис.1), исходят из уравнения второго закона Кирхгофа для мгновенных значений напряжений: u = u_Rк+u_L+u_C .

Рис.1

Если к цепи приложено напряжение

u = U_m sin (t + _u) = U_msin t ,

то мгновенный ток становится равным

i = I_m sin (t + _i) = I sin (t + _i) ,

где I_m и I = - соответственно амплитудное и действующее значения тока.

Расчет в цепях переменного тока производят символическим методом по действующим значениям тока и напряжения.

52

В комплексной форме

;

(R_к + jX_L) - jX_C = [R_к+ j(X_L - X_C)] = (R_к + jX) =

= Z = Ze ^j ,

где X_L = L = 2fL- индуктивное сопротивление катушки;

X_C = 1/C = 1/ 2fC - емкостное сопротивление;

X = X_L - X_C - реактивное сопротивление цепи;

Z_к = R_к + jX_L = Z_кe ^jк - комплексное сопротивление катушки индуктивности;

Z = R + jX = Ze ^j - комплексное сопротивление цепи;

Z = - модуль комплексного сопротивления, представляющий полное сопротивление неразветвленной цепи;

 = _u - _i = arctg (X/ R_к) - угол сдвига фаз между напряжением и током, определяемый из треугольника сопротивлений цепи.

Из предыдущего уравнения комплекс тока равен:

= .

Модуль комплексного тока I определяет действующее значение тока в цепи: I = .

В зависимости от соотношения X_L и X_C полное сопротивление цепи Z может носить активно-индуктивный (X_L  X_C), активно-емкостный (X_L X_C) или чисто активный (X_L = X_C) характер. Векторные диаграммы напряжений при различных нагрузках приведены на рис.2.

Понятия мгновенной, активной, реактивной, полной мощностей, соотношений между ними описаны в лабораторной работе № 5.

В неразветвленной цепи (рис.1) активная мощность P = UI cos  = U_RкI = =R_кI² = P_к выделяется на активном сопротивлении катушки. При взаимной компенсации напряжений U_L и U_C (рис.2,б) имеет место резонанс напряжений.

Условием резонанса напряжений является равенство реактивных сопротивлений : 2f₀L = .

53

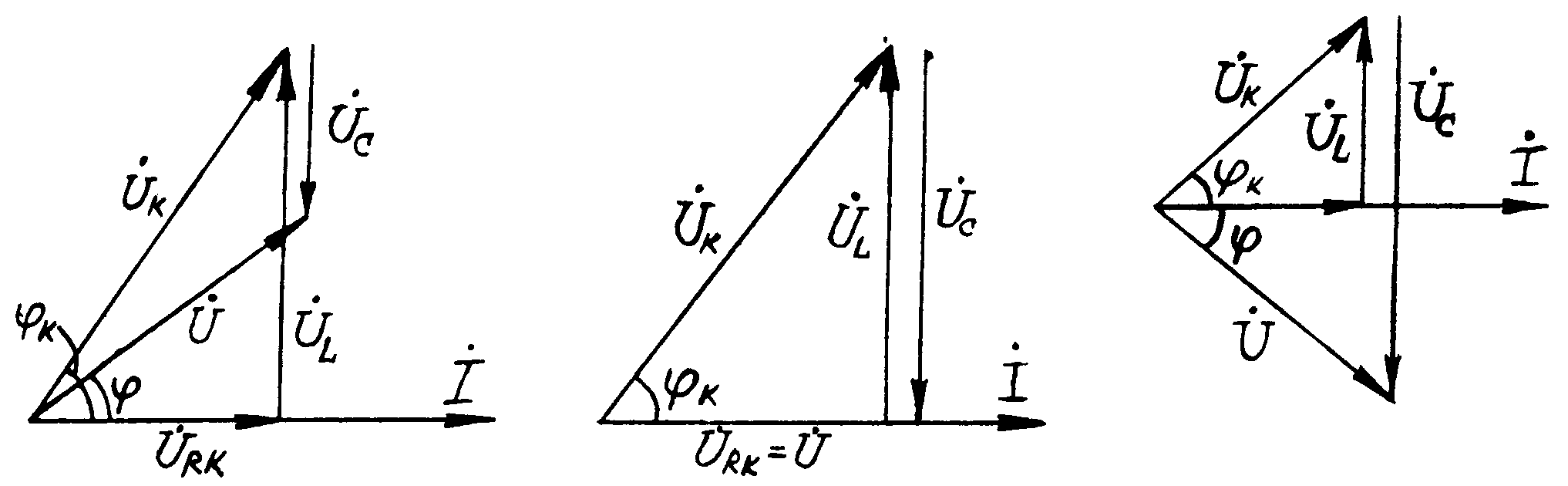
X_L  X_C ;   0 X_L = X_C ;  = 0 X_L X_C ;   0

а б в

Рис.2

Из условия резонанса напряжений определяется резонансная частота:

f₀ = .

При резонансе напряжений полное сопротивление цепи Z = R_к , действующее значение тока (I₀ = U/ R_к ) достигает наибольшего значения, сдвиг по фазе между током и напряжением отсутствует:  = 0 , цепь носит чисто активный характер, из сети потребляется только активная мощность P = UI₀ , она максимальна.

Если R X_L0 и R X_С0 , то при резонансе действующие напряжения на реактивных элементах, равные:

U_L0 = X_L0I₀ = (X_L0 / R_к)U ; U_C0 = X_C0I₀ = (X_С0/ R_к)U,

превышают приложенное напряжение U. Это превышение напряжений (U_L0 = =U_C0 ), по сравнению с U, характеризует добротность цепи q:

q = U_L0/ U = U_С0/ U = X_L0 / R_к = X_С0/ R_к .

Реактивное сопротивление при резонансной частоте называют волновым или характеристическим сопротивлением цепи:

Z_в = 2f₀L = 1/ 2f₀C = .

Добиться резонанса напряжений в цепи, как следует из условия резонанса, можно изменением параметров цепи L, C, частоты f.

Описание установки

Экспериментальное исследование линейной неразветвленной электрической цепи выполняют на установке, электрическая схема которой приведена на рис.3.

54

Питание цепи осуществляется через понижающий трансформатор. Клем- мы трансформатора через пакетный переключатель подсоединяются к фазе напряжения трехфазной сети.

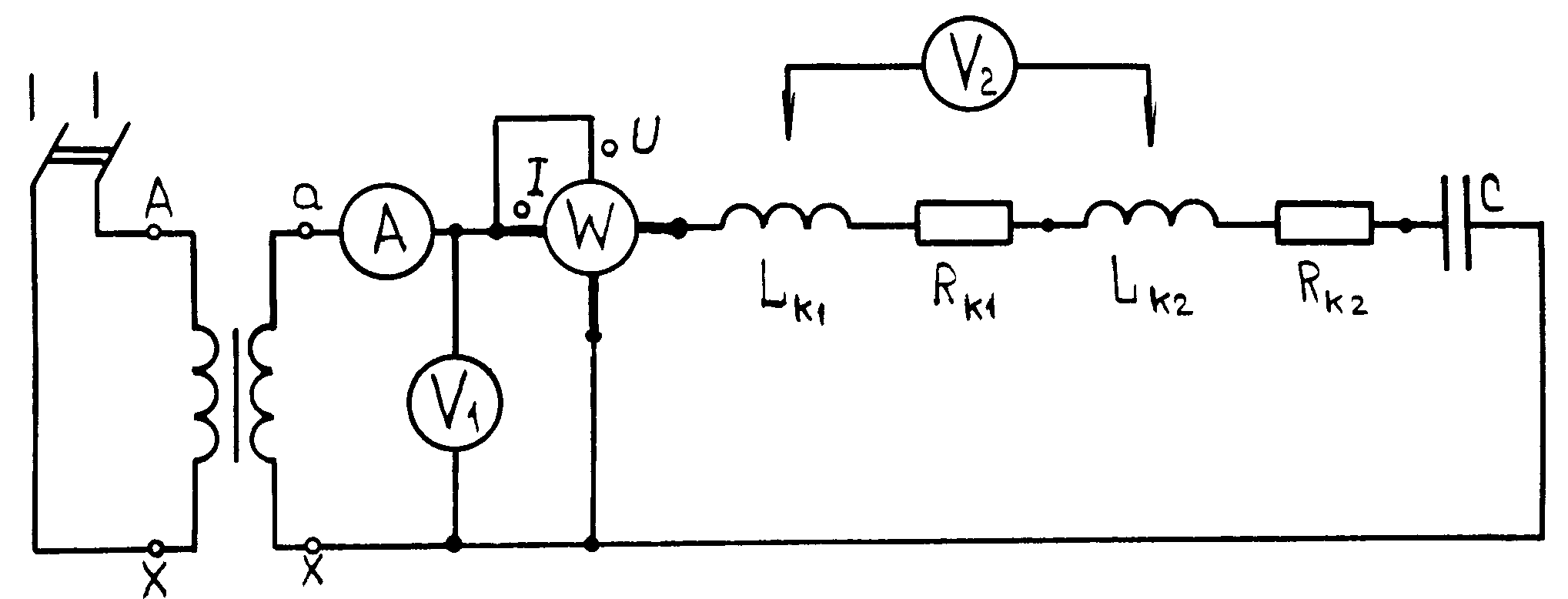
Рис.3

Горизонтальное положение рукоятки пакетного переключателя соответствует выключенному состоянию. Напряжение вторичной обмотки трансформатора подается на исследуемую цепь (клеммы аx). Установка состоит из пакетного переключателя, понижающего лабораторного автотрансформатора, двух индуктивных катушек, добавочного резистора R, батареи конденсаторов. За исключением вольтметра V₁, в установке применены приборы настольного исполнения. Вольтметр V₁ предназначен для измерения напряжения на входных клеммах исследуемой цепи. Многопредельный вольтметр V₂ служит для измерения напряжения на катушке индуктивности и конденсатора. Ваттметр и амперметр предназначены для измерения активной мощности и тока.

Порядок выполнения работы

1. Ознакомиться с приборами и оборудованием экспериментальной установки и записать технические характеристики в отчет.

2. Собрать цепь из двух последовательно соединенных катушек индуктивности и батареи конденсаторов. Изменяя емкость батареи конденсаторов, добиться резонанса напряжений, при котором ток достигает максимального значения и активная мощность P = S = UI. Зафиксировать резонансную мощность.

3. Произвести опыты, изменяя емкость от 0 до С_р (3…4 опыта) и в таких же пределах выше С_р (3…4 опыта). Вблизи резонансной емкости измерения делать чаще. Данные измерений занести в табл. 1.

4. Произвести необходимые вычисления. Учитывая, что параметры катушек не изменялись, достаточно их рассчитать один раз.

55

При резонансе определить добротность цепи и данные занести в табл.1 . Таблица 1

№ Данные наблюдений

Результаты вычислений

С, мкФ

U, В

I, А А

Р, Вт

Uк , B

Uс , B

S, ВА

Q , ВАр

cos

Z, Oм

Rк , Ом

Xк , Ом

Xc , Ом

X , Ом

q

19

5. Уменьшить индуктивность цепи. Для этого отключить вторую катушку с R_кz ,L_кz , замкнув ее перемычкой накоротко. Изменяя емкость батареи конденсаторов, снова найти С_р , при которой в цепи возникает резонанс напряжений. Произвести измерения аналогично п.3, данные занести в табл. 2.

Таблица 2

№	Данные наблюдений						Вычислено
	С, мкФ	U, В	I, А	Р, Вт	Uк , В	Uc , В	Z	Rк1	Xк1	q
1:9

6. По данным табл. 2 рассчитать параметры катушки X_к1 , R _к1, добротность цепи q. Так как параметры катушки не изменяются, достаточно рассчитать их один раз, например при резонансе напряжений. Записать формулу для определения резонансной емкости C_рез. Объяснить изменение C_рез в п.3 и п.5.

7. По данным табл. 1 и 2 для исследуемой цепи построить на одном графике для каждой зависимости U_к , U_c , I от емкости С батареи конденсаторов. По расчетным данным табл. 1 построить зависимости S , cos  на одном графике от величины емкости батареи конденсаторов. Сделать выводы о влиянии частоты питающей сети и емкости на определяемые параметры. Сравнить теоретические кривые и полученные на основании экспериментальных данных.

8. Построить в масштабе по опытным данным табл. 1 векторные диаграммы напряжений и тока для трех состояний цепи: до резонанса, при резонансе и после резонанса.

Указание. При построении векторной диаграммы напряжений (см. рис.2) вектор тока совмещают с действительным направлением оси +I комплексной плоскости. Напряжение на катушке опережает ток на угол _к , определяемый параметрами катушки индуктивности:

Z_к = ; R_к = ; X_к = ; _к = arccos .

56

Для построения вектора необходимо определить угол _к или составляющие напряжения катушки: активную U_Rк = R_к I, совпадающую с током, и индуктивную U_Lк = X_Lк I , опережающую ток на угол  /2 . Сдвиг по фазе между током и напряжением на конденсаторе _c = -  /2. Обратить внимание, что при резонансе  , так как лишь индуктивная составляющая напряжения катушки равна напряжению на конденсаторе: U_L = U_c.

Вопросы для самоконтроля

1. От каких величин зависит значение угла сдвига фаз между напряжением и током?

2. Что называется индуктивным и емкостным сопротивлениями, от чего они зависят?

3. Каким способом можно измерить величины индуктивности и емкости реактивных приемников?

4. От каких величин зависит полное сопротивление электрической цепи?

5. Как рассчитать действующее значение тока в неразветвленной части цепи с приемниками, характеризуемыми сосредоточенными параметрами R, L и С?

6. Каково условие резонанса напряжений?

7. Как определяется резонансная частота, резонансная емкость?

8. Дать понятие добротности контура.

9. Как рассчитывают активную, реактивную и полную мощность в линейной электрической цепи синусоидального тока?

10. Для последовательной цепи, состоящей из R, L и С при постоянном значении действующего напряжения на зажимах цепи вывести и проанализировать зависимости I , U_к , U_с , S от емкости С и частоты генератора f.

11. Как по известным параметрам R, L, C определить напряжения на отдельных элементах и участках цепи и построить векторные диаграммы напряжений?

Список литературы

1. Электротехника / Под ред. В. Г. Герасимова. – М.: Высшая школа, 1985. –

С. 68-73, 81-86.

2. Касаткин А. С., Немцов М. В. Электротехника. – М.: Энергоатомиздат, 1983. –

С. 57-84, 94-97.

3. Иванов А.А. Электротехника: Лабораторные работы. – Киев: Вища школа, 1976. – С. 60-67.

3. Бессонов Л. А. Теоретические основы электротехники. – М.: Высшая школа,

1984. – С. 76-93, 95-96.

57

Лабораторная работа № 7

Исследование однофазного трансформатора

Цель работы:

1. Изучить устройство, принцип работы трансформатора.

2. Определить коэффициент трансформации и напряжение короткого замыкания трансформатора.

3. Построить внешние характеристики трансформатора при различных нагрузках (активной, активно-индуктивной, емкостной).

4. Определить параметры схемы замещения трансформатора.

Основные теоретические положения

Трансформатором называют статическое электромагнитное устройство, предназначенное для преобразования посредством магнитного потока электрической энергии переменного тока одного напряжения в электрическую энергию переменного тока другого напряжения при неизменной частоте.

Электромагнитная схема трансформатора (а) и условные графические обозначения трансформатора (б, в) изображены на рис.1. На замкнутом магнитопроводе, набранном из листов электротехнической стали, расположены две обмотки. Первичная обмотка с числом витков W₁ подключается к источнику электрической энергии с напряжением U₁. Вторичная обмотка с числом витков W₂ подключается к нагрузке.

Под действием подведенного переменного напряжения U₁ в первичной обмотке возникает ток i₁ и появляется изменяющийся магнитный поток Ф. Этот поток индуцирует ЭДС e₁ и e₂ в обмотках трансформатора:

e₁ = - W₁ ; e₂= - W₂ .

ЭДС e₁ уравновешивает основную часть напряжения источника U₁ , ЭДС e₂ создает напряжение U₂ на выходных зажимах трансформатора.

При замыкании вторичной цепи ток вторичной обмотки i₂ создает собственный магнитный поток. Намагничивающие силы токов первичной и вторичной обмоток определяют результирующий рабочий магнитный поток, сцепленный с витками первичной и вторичной обмоток.

Небольшая часть магнитного потока сцеплена только с витками первичной обмотки. Эту часть потока называют потоком рассеяния первичной обмотки и обозначают Ф_1. Аналогично образуется магнитный поток рассеяния вторичной обмотки Ф_2.

58

к приемнику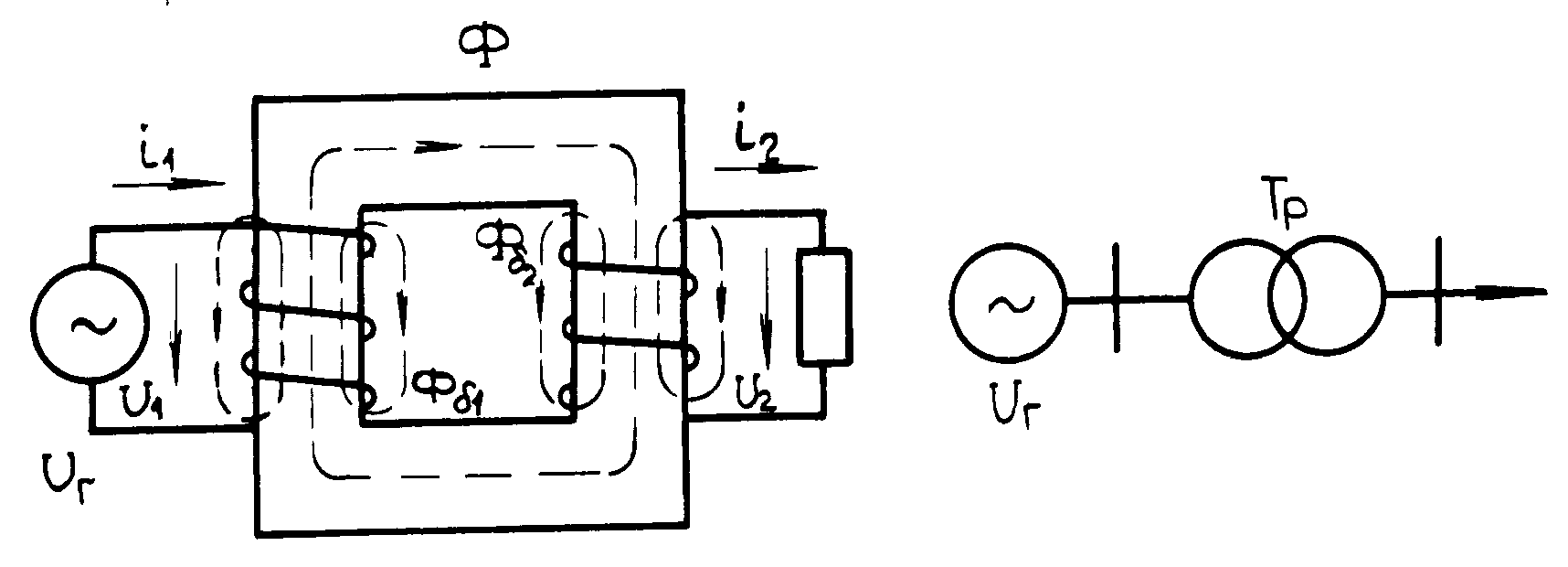

а б

в

Рис.1

Рис.2

Магнитные потоки рассеяния наводят в соответствующих обмотках переменные ЭДС е_1 и е_2 . ЭДС рассеяния можно заменить падением напряжения на индуктивном сопротивлении рассеяния:

.

При изучении эксплуатационных свойств трансформатора следует учитывать активные сопротивления обмоток трансформатора R₁ и R₂. Тогда уравне-

59

ния электрического состояния обмоток трансформатора примут вид

- ЭДС, возбуждаемые рабочим потоком Ф;

- напряжение на вторичной обмотке трансформатора.

Так как величина мала, составляет не более единиц процентов от , то

U₁ Е₁ = W₁Ф = 4,44 f W₁Ф_m , (1)

где f – частота напряжения сети;

Ф_m - амплитудное значение магнитного потока в трансформаторе.

Из выражения (1) видим, что при постоянной величине U₁ магнитный поток Ф почти не изменяется, а значит незначительно меняется суммарная магнитодвижущая сила первичной и вторичной обмоток:

W₁ + W₂ = W₁ ,

или, обозначив , получим уравнение токов трансформатора:

= + ,

где - ток первичной обмотки в режиме холостого хода.

Для построения схемы замещения реальный трансформатор заменяют приведенным. У приведенного трансформатора число витков первичной обмотки равно числу витков вторичной: W₁ = W₂. При замене реального трансформатора приведенным параметры первичной обмотки остаются неизменными, а параметры вторичной - приводятся к первичной. Параметры вторичной цепи приведенного трансформатора обозначаются так же, как и у реального, лишь снабжаются штрихом. Итак, уравнения приведенного трансформатора примут вид

= + .

Данным уравнениям соответствует Т-образная схема замещения трансформатора (рис.2).

60

Так как I_1x составляет единицы процентов от I_1ном , то Т-образную схему можно заменить на Г-образную (рис.3) или упрощенную (рис.4), где

R_к = R₁ + R₂ ; X_к = X_1 + X_2 ; R_x = R₀ + R₁ ; X_x = X₀ + X_1 .

Рис.3 Рис.4

Параметры схем замещения определяются по данным опыта холостого хода (U_1н , I_1x , P_x) и опыта короткого замыкания (U_к , I_1н , P_к):

Z_x = ; R_x = ; Z_к = ; R_к = ;

X_x = ; X_к = .

Для определения параметров Т-образной схемы замещения упрощенно принимают: R₁ R₂ = ; X_1 = X_2 = .

Коэффициентом трансформации называется соотношение ЭДС e₁ и e₂

= К .

Для трансформатора, работающего в режиме холостого хода, с достаточной для практики точностью можно считать, что

К  . (2)

Процентное изменение вторичного напряжения U₂  при переменной нагрузке определяется так: U₂  = , (3)

где U_2x и U₂ - соответственно вторичные напряжения при холостом ходе и заданной нагрузке.

61

У трансформаторов средней и большой мощности U_2x и U₂ мало отличаются друг от друга, использование формулы (3) приводит к значительным погрешностям, поэтому процентное изменение вторичного напряжения рассчитывается по формуле

U₂  =  (U_каcos ₂ + U_кр sin ₂) , (4)

где  = - коэффициент нагрузки; I₂ и I_{2 ном} - соответственно фактический и номинальный ток во вторичной обмотке;

U_ка и U_кр - соответственно активная и реактивная составляющие напряжения короткого замыкания.

U_к  = ,

где U_к - напряжение в опыте короткого замыкания при номинальном токе в первичной обмотке.

U_ка = U_к  cos _к = U_к  ; U_кр = .

Характеристики трансформаторов изображены на рис.5 и 6.

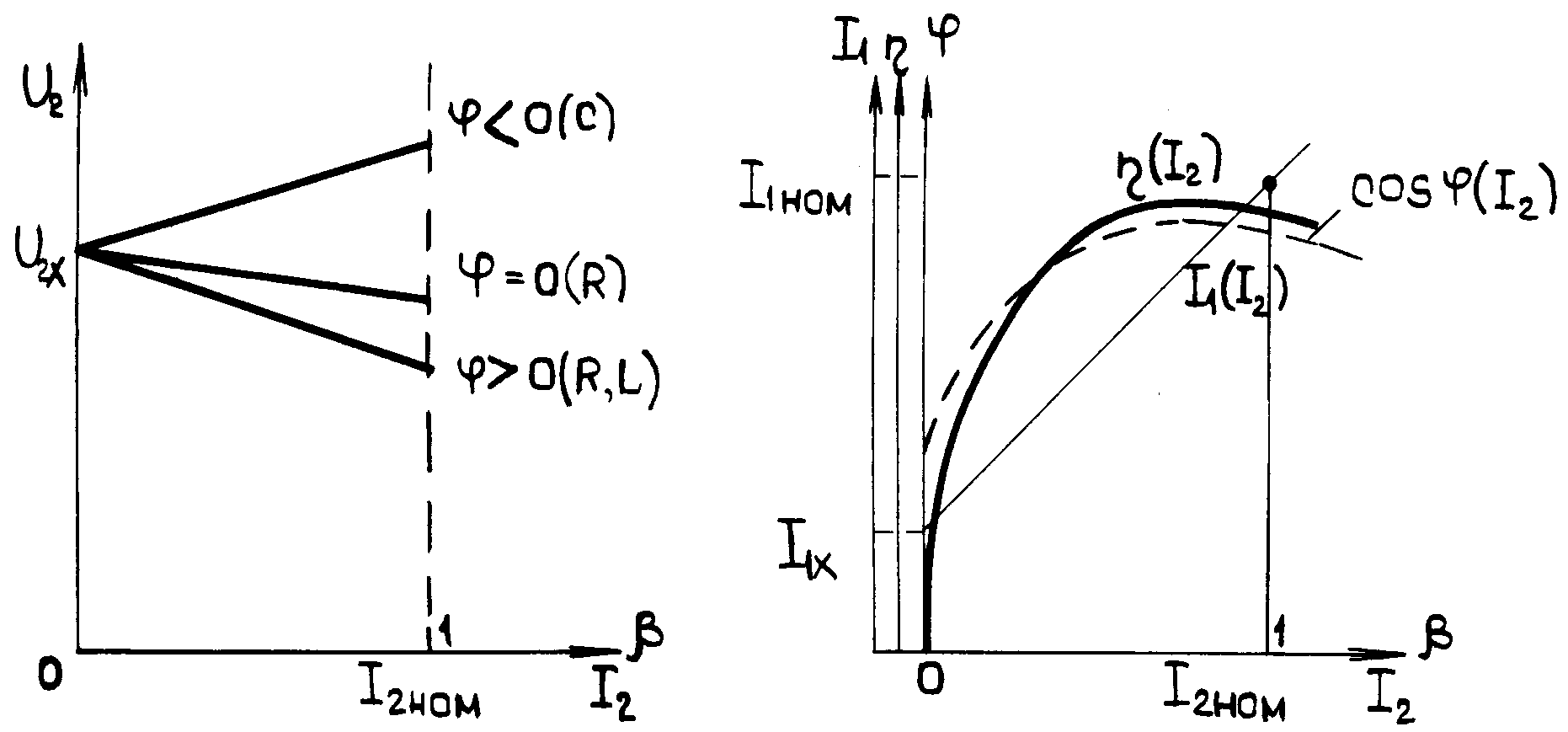
Рис.5 Рис.6

Внешние характеристики (рис.5) можно объяснить с применением формулы (4).

Увеличение напряжения при емкостной нагрузке кроме формулы (4) можно объяснить с помощью упрощенной схемы замещения трансформатора (рис.7). В последовательном контуре при увеличении емкости напряжение на конденсаторе изменяется по кривой (рис.8).

62

Рис.7 Рис.8

Напряжение на конденсаторе равно напряжению U₂. Из рис.8 видно, что с увеличением емкости, а значит, с увеличением тока I₂ = U₂ / X_c = U₂C напряжение на зажимах трансформатора увеличивается.

Коэффициент мощности cos ₁ трансформатора определяют по формуле

cos ₁ = .

Коэффициент полезного действия трансформатора может быть определен экспериментальным путем:

 = , где P₂ = U₂I₂ cos ₂ .

Прямой метод определения КПД допустим для трансформаторов малой мощности. КПД трансформаторов средней и большой мощности определяют косвенным путем, используя данные опытов холостого хода и короткого замыкания по формуле

 = , (5)

где  = ; S_ном - номинальная мощность трансформатора;

cos ₂ - коэффициент мощности приемников;

P_x и P_к - активные мощности соответственно при опыте холостого хода и короткого замыкания.

63

Описание лабораторной установки

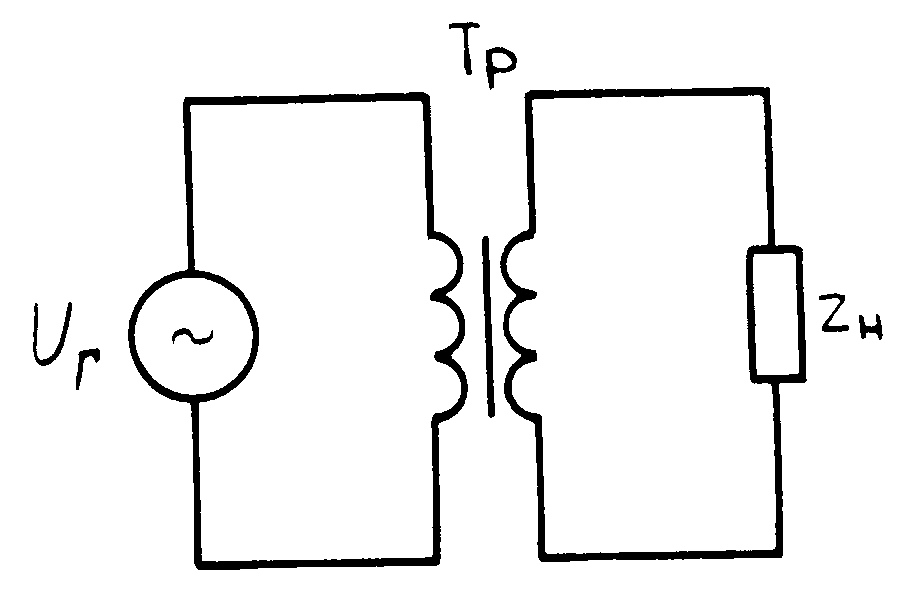
Экспериментальное исследование однофазного трансформатора выполняется на установке (рис.9), где со стороны первичной обмотки АX трансформатора ТР предусмотрены приборы для измерения подводимого напряжения U₁, тока I₁ и активной мощности P₁. Со стороны вторичной обмотки ах соответствующими приборами измеряют вторичное напряжение U₂ и ток нагрузки I₂, создаваемый при активной нагрузке – резисторами R₁, R₂, R₃; при активно-индуктивной – дросселями с параметрами R_к , L; при емкостной нагрузке – конденсаторами С₁, С₂, С₃. Для проведения опыта короткого замыкания предусмотрены клеммы К₁, К₂.

Параметры трансформатора: U_1н = 220 В ; U_2н = 100 В; S_1н = S_2н = 100 ВА. Активное сопротивление дросселя: R_к = 10 Ом.

Питание установки осуществляется от сети переменного напряжения через двухполюсный выключатель В и регулирующий автотрансформатор ЛАТР.

Порядок выполнения работы

1. Ознакомиться с приборами, аппаратами и оборудованием экспериментальной установки и записать их технические характеристики.

2. Исследовать трансформатор в режиме холостого хода и нагруженном режиме.

Для этого необходимо следующее:

- выключатель “B” должен находиться в положении “Выкл.”;

- поворотом влево ручки регулируемого автотрансформатора ЛАТР “Рег. U₁” установить в нулевое положение;

- клеммы К₁ и К₂ – разомкнуты;

- все тумблеры вторичной обмотки трансформатора В_1…В₉ – в положении “Выкл.”.

После проверки правильности подготовки к проведению опыта включить выключатель В, ручкой регулирующего автотрансформатора “Рег. U₁” установить номинальное напряжение первичной обмотки трансформатора и записать показания всех приборов в табл. 1 для режима холостого хода.

Нагрузить трансформатор, включая тумблеры В₁ , В₂ , В₃. После каждого включения занести показания приборов в табл. 1 для активной нагрузки; выключить тумблеры В₁, В₂ , В₃.

64

Рис.9

Нагрузить трансформатор на активно-индуктивную нагрузку, включая тумблеры В₄ , В₅ , В₆ , и после каждого включения записать показания приборов в табл. 1 для активно-индуктивной нагрузки; отключить активно-индуктивную нагрузку, установив тумблеры В₄ , В₅, В₆ в положение “Выкл.”.

Аналогичные измерения произвести при емкостной нагрузке, данные занести в табл. 1.

Таблица 1

№

Измерено

Вычислено

Режим

U1 , B

I1 , A

P1 , Вт

U2 , B

I2 , A

cos1

cos2

P2 , Вт





U,

1.

Холостой ход

2. 3.4.

Активная нагрузка

5.6. 7.

Активно-ин- дуктивная нагрузка

8. 9. 10

Емкостная нагрузка

65

Разомкнуть все тумблеры вторичной цепи трансформатора.

Поворотом влево установить ручку регулирующего автотрансформатора в нулевое положение.

Выключить однополюсный выключатель В.

3. Опыт короткого замыкания.

Перед опытом необходимо проверить, чтобы ручка регулирующего автотрансформатора находилась в нулевом положении.

Замкнуть накоротко вторичную обмотку трансформатора (клеммы К₁ и К₂ замкнуть проводником).

Включить однополюсный выключатель В. Плавно увеличивая напряжение первичной обмотки трансформатора, установить номинальный ток первичной обмотки , показания приборов занести в табл. 2. Поворотом влево установить ручку регулирующего автотрансформатора в нулевое положение; установить выключатель В в положение “Выкл.”, убрать закоротку между клеммами К₁ и К₂.

Данные эксперимента показать преподавателю.

4. Определить коэффициент трансформации К.

5. По данным таблицы рассчитать cos ₁ , cos ₂ , P₂ ,  , U , .

6. Построить в общей системе координат характеристики трансформатора при активной нагрузке в функции вторичного тока:

I₁= f (I₂) , cos ₁= f (I₂) ,  (I₂) при U₁ = U_1н= const.

Характерный вид зависимостей приведен на рис.6.

7. В одной системе координат построить внешние характеристики трансформатора U₂= f (I₂) или U₂= f () при различных нагрузках (рис.5).

8. Рассчитать параметры Г-образной схемы замещения трансформатора и заполнить табл. 3.

Таблица 2

Напряжение Uк , В	Ток А I , А	Активная мощность P, Вт

Таблица 3

Rx , Ом	Xx , Ом	Rк , Ом	Xк , Ом

66

9. Начертить Т-образную схему замещения трансформатора. Пояснить, почему экспериментально нельзя определить все параметры Т-образной схемы замещения трансформатора.

10. Сделать вывод по результатам выполненной работы.

Контрольные вопросы

1. Как устроен трансформатор?

2. От чего зависят ЭДС обмоток трансформатора и каково их назначение?

3. В каких случаях трансформатор называют повышающим и в каком - понижающим?

4. Что называют коэффициентом трансформации?

5. Какие вы знаете номинальные параметры трансформатора и что они определяют?

6. Как определить номинальные токи обмоток трансформатора, если известна номинальная мощность трансформатора?

7. Что называют внешней характеристикой трансформатора и как ее получить?

8. Как найти процентное изменение вторичного напряжения трансформатора для заданной нагрузки?

9. Какие потери энергии имеются в трансформаторе, от чего они зависят и как определяются?

10. Для чего магнитопровод трансформатора набирается из листов электротехнической стали и какой толщины эти листы?

11. Какие вы знаете схемы замещения трансформатора и как определяются их параметры?

12. Как проводится опыт холостого хода? Какие параметры этого опыта указываются в паспорте трансформатора?

13. Как проводится опыт короткого замыкания трансформатора? Какие параметры этого опыта указываются в паспорте трансформатора?

14. Где на практике учитывается величина напряжения короткого замыкания?

15. Чем конструктивно отличаются автотрансформаторы от трансформаторов обычной конструкции?

Список литературы

1. Электротехника / Под ред. В. Г. Герасимова. – М.: Высшая школа, 1985. – С. 237-260.

2. Касаткин А. С., Немцов М. В. Электротехника. – М.: Энергоатомиздат, 1983. – С. 166-198.

67

Корректор М.И. Прокушкина

Изд-во ИжГТУ, Лицензия РФ ЛР № 020885 от 24.05.99.

Подписано в печать 21.05.2001. Бумага офсетная. Формат 60х84/16

Печать офсетная. Усл. Печ. Л. 3,64. Уч.-изд. Л. 4,07. Тираж 50 экз. Заказ № 30

Тип. Издательства ИжГТУ. Лицензия РФ Пд № 00525 от 28.04.2000.