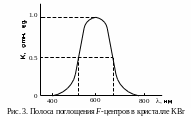
Положение, интенсивность и полуширина f-полосы

В спектре оптического поглощения F-центры регистрируются по соответствующей полосе поглощения (рис. 3). Полоса поглощения F-центров (F-полоса) характеризуется интенсивностью (коэффициент поглощения, см^–1), положением в спектре (частота в эВ или длина волны λ_max в нм) и полушириной (Н, в эВ).

Исходя из классической теории дисперсии и поглощения, Смакула [1] получил следующую формулу для описания полосы поглощения осциллятора:

,

где К – коэффициент поглощения; – концентрация затухающих осцилляторов (в данном случае F-центров); с – скорость света в вакууме; ε₀ – диэлектрическая постоянная вакуума; е и m – заряд и масса электрона; n – показатель преломления кристалла; Н – полуширина полосы поглощения; – логарифмический декремент затухания осциллятора; v₀ и v – собственная и текущая частота электромагнитных колебаний. Соотношение позволяет судить о форме спектральной полосы поглощения и позволяет оптическим путем определять число поглощающих осцилляторов в единице объема , поэтому оно лежит в основе количественного абсорбционного спектрального анализа.

Как правило, в поглощении участвуют не все осцилляторы. Доля участвующих в поглощении осцилляторов учитывается числом, называемым «силой осциллятора»: . После введения f в соотношение получаем формулу, обычно используемую для определения концентрации поглощающих центров:

.

Если коэффициент поглощения в максимуме полосы поглощения (К) измеряется в см^–1, Н – в эВ, то формула принимает вид:

.

Для ряда ионных кристаллов сила осциллятора f для F-полосы и показатель преломления приведены в таблице 3.

Таблица 3

	LiF	NaF	NaCl	KCl	KBr	KI
n	1,42	1,34	1,56	1,49	1,66	1,65
f	0,55	0,57	0,58	0,57	0,51	0,55

Порядок выполнения работы

1. Получить исследуемые кристаллы у преподавателя или лаборанта.

2. Измерить толщину кристаллической пластинки.

3. Подготовить спектрофотометр СФ-26 к работе согласно описанию.

4. Установить образец в кристаллодержатель и провести измерения спектра поглощения K = K(λ) в диапазоне 200–1100 нм с интервалом 10 нм.

При расчетах функции K = K(λ) необходимо использовать закон Буггера-Ламберта:

J = J₀ exp(– kx),

где J₀ и J – интенсивности падающего и прошедшего через образец монохроматических световых потоков; х – толщина поглощающего слоя. Величина

T = J / J₀ · 100%

называется пропусканием, величина

OD = ln (J₀ / J)

называется оптической плотностью.

5. После облучения образца на гамма-установке «Исследователь» в течение 30 мин снова провести измерение спектра поглощения в диапазоне 200–1100 нм с интервалом 5 нм и занести данные измерений в таблицу 4.

Таблица 4

Экспериментальные данные

λ, нм	200	205	210	215	220	и т.д.
ν, эВ	6,1725	6,022	5,878	5,742	5,611
К, см-1

6. На основе данных таблицы 4 построить спектры поглощения K = K(λ) и K = K(v).

7. Положение полос поглощения электронных центров окраски в ЩГК описывается модифицированным соотношением Моллво-Айви:

v₀₁ · d · x^m = C₀₁ (эВ·А²),

где d – расстояние между ближайшими ионами кристалла; х – электроотрицательность по Полингу; m – параметр; С₀₁ – постоянная, следующая из модели бесконечно глубокой ямы, локализовавшей электрон, равная 27,33 эВ·А². Используя формулу и данные таблицы 5, идентифицировать в измеренном спектре F-полосу.

Таблица 5

Кристалл	LiF	NaF	NaCl	KCl	KBr	KI
d, A	2,014	2,31	2,82	3,15	3,30	3,53
x	4	4	3	3	2,8	2,5
m	0,25	0,25	0,25	0,25	0,25	0,25

8. Определить интенсивность (К^макс) и полуширину (Н, эВ) F-полосы.

9. По формуле рассчитать концентрацию F-центров.

10. Рассчитать поглощенную дозу гамма-излучения по формуле

D = J · t,

где J = 110 рад/с (1 рад = 100 эрг/г).

11. Пользуясь полученным значением концентрации F-центров и формулой , определить энергию (эВ), затрачиваемую на накопление одного F-центра.

Вопросы и задания

1. Какие дефекты называются радиационными?

2. Дать определение электронных и дырочных центров окраски.

3. В чем заключается различие между H – и V_{k –} центрами?

4. Как определяется концентрация радиационных дефектов по спектрам поглощения?

Литература

1. Поль Р.В. Оптика и атомная физика. – М.: Наука, 1966. – Гл. 12, 13, 18.

2. Киттель Ч. Введение в физику твердого тела. – М.: Наука, 1978. – Гл. 19.

3. Пикаев А.К. Современная радиационная химия. Твердое тело и полимеры. Прикладные аспекты. – М.: Наука, 1987. – 448 с.

Лабораторная работа № 3

Тарировка пьезоэлектрического детектора

Цель работы: ознакомиться с методом тарировки пьезоэлектрических датчиков и провести тарировку пьезодетектора на основе пьезокерамики ЦТС-19.

Принадлежности: металлический столик с укрепленными на нем держателем пьезоэлемента, стойкой, рычагом передачи давления на пьезоэлемент, маятником, угломерным инструментом; кабель, осциллограф С8-12, С8-13.

Введение

Появление поляризации в диэлектрике под действием механических напряжений называется прямым пьезоэффектом. Кроме прямого пьезоэффекта существует и обратный. Он заключается в том, что при наложении внешнего электрического поля кристалл несколько сжимается или расширяется. Пьезоэффект наблюдается во всех нецентросимметричных кристаллах. Под действием механических напряжений происходит смещение заряженных частиц и таким образом возникает дипольный момент. Смещение частиц в кристаллах с центром симметрии не приводит к появлению поляризованного состояния, так как в этом случае в силу наличия центра симметрии происходит электрическая компенсация моментов, образованных за счет смещения положительно и отрицательно заряженных частиц.

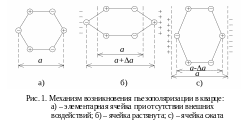
Рассмотрим механизм возникновения пьезополяризации на примере кварца. На рис. 1 изображена гексагональная элементарная ячейка SiO₂, в которой имеет место чередование положительных и отрицательных ионов. В отсутствии внешних напряжений дипольный момент ячейки равен нулю. Пусть под действием механического напряжения элементарная ячейка растягивается (рис. 1, б). Такая деформация приводит к появлению дипольного момента P = qΔa, где q – заряд ионов, a – величина растяжения ячейки, при сжатии ячейки знак дипольного момента меняется: P = – qΔa. Если одноосное напряжение, например напряжение растяжения, приложено к кристаллу кварца вдоль одной из осей второго порядка, то величина дипольного момента определяется соотношением

P = dσ,

где d – так называемый пьезоэлектрический модуль.

В общем случае напряженное состояние характеризуется тензором второго ранга с девятью компонентами. Экспериментально установлено, что, когда произвольное напряжение действует на нецентросимметричный кристалл, каждая компонента поляризации P_i линейно связана со всеми компонентами тензора напряжений σ_ij:

.

Аналогичные уравнения можно написать для P₂ и P₃. Таким образом, в общем виде

P_i = d_ijk σ_jk ,

где d_ijk – тензор пьезоэлектрических модулей (тензор третьего ранга).

Кроме кварца пьезоэлектрическими свойствами обладают такие широко используемые в технике кристаллы, как КДР – дигидрофосфат калия (KH₂PO₄), АДР – дигидрофосфат аммония (NH₄H₂PO₄), а также различные виды пьезокерамики. Пьезоэлектрики находят применение в качестве мощных излучателей и чувствительных приемников ультразвука, стабилизаторов частоты, электрических фильтров высоких и низких частот, трансформаторов напряжений и тока.

Протарировать пьезоэлекрический датчик – значит поставить показания пьезодетектора в соответствие с давлением в абсолютных единицах. Необходимость измерения давления в широком диапазоне частот возникла в связи с возрастанием роли акустических методов исследования твердых тел и все возрастающим применением акустических методов в технике. В области высоких частот величина механических смещений столь мала, что их непосредственное измерение затруднено. Поэтому обычно используются различные косвенные методы измерения давления.

В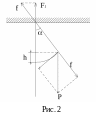 данной работе тарировка осуществляется методом нормированного давления с помощью математического маятника. Движение математического маятника описывается гармонической функцией, позволяющей рассчитать величину силы, действующей на точку подвеса нити маятника. Величина силы, действующей на точку подвеса, когда маятник находится в крайнем положении и в нижней точке траектории движения, рассчитывается следующим образом (рис. 2):

F₁ = f cos α = P cosα · cosα = mg cos²α , P = mg. (4)

Потенциальная энергия рассчитывается по формуле

W = mgh = mg (L – L cosα ). (5)

С огласно рис. 3.

, (6)

где mg – вес маятника, – центробежная сила.

Из закона сохранения энергии можно записать следующее выражение:

V² = 2gh . (7)

Величина изменения давления, действующего на пьезоэлемент, определяется как

ΔF = F₂ – F₁. (8)

Для численного определения пьезомодуля необходимо учесть величину электрической емкости пьезоэлемента и токосъемного кабеля.

Расчет пьезомодуля ведется по формуле:

, (9)

где С – значение электрической емкости кабеля и пьезоэлемента; U – величина электрического напряжения на электродах пьезоэлемента; ΔF – величина силы, действующей на пьезоэлемент; d – пьезомодуль пьезоэлемента.