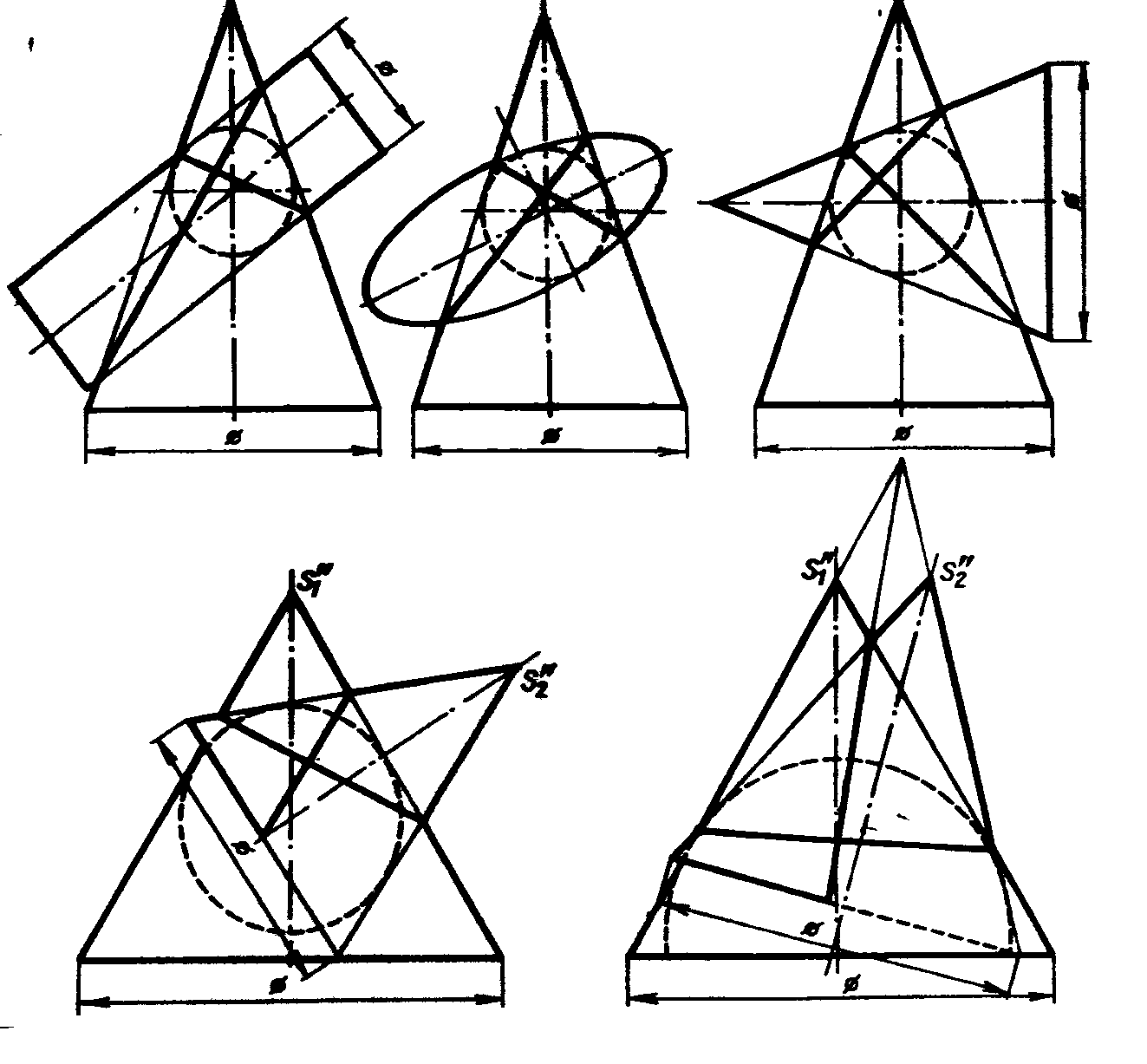4. Построение линии пересечения поверхностей способом вспомогательных концентрических сфер.
Этот способ применяется для построения линии пересечения двух поверхностей при условиях:
Пересекаются поверхности вращения произвольного вида;
Оси симметрии поверхностей пересекаются;
оси поверхностей параллельны одной из плоскостей проекций (это условие легко создать, используя методы преобразования плоскостей проекций).
Основой способа концентрических сфер является свойство сферы, имеющей центр на оси поверхности вращения, пересекать ее по окружности. Пусть даны два усеченных конуса с пересекающимися осями в точке О, имеющих общую плоскость симметрии относительно фронтальной плоскости проекций (Рис.10).Построим сферу произвольного радиуса из центра О, которая отобразится окружностью. Эта сфера соосна как с одной, так и с другой поверхностью, а поэтому пересечет каждую по окружности. На чертеже эти окружности отобразятся отрезками прямых. В их взаимном пересечении получим точки, которые принадлежат обеим поверхностям и, значит, искомой линии пересечения. Изменяя радиус сферы. Можно получить какое угодно число точек линии пересечения. Причем в начале решения надо выбрать радиусы наибольшей и наименьшей сфер, пересекающих обе поверхности так, чтобы получались общие точки. Для этого нужно отметить точки пересечения очерковых образующих поверхностей.
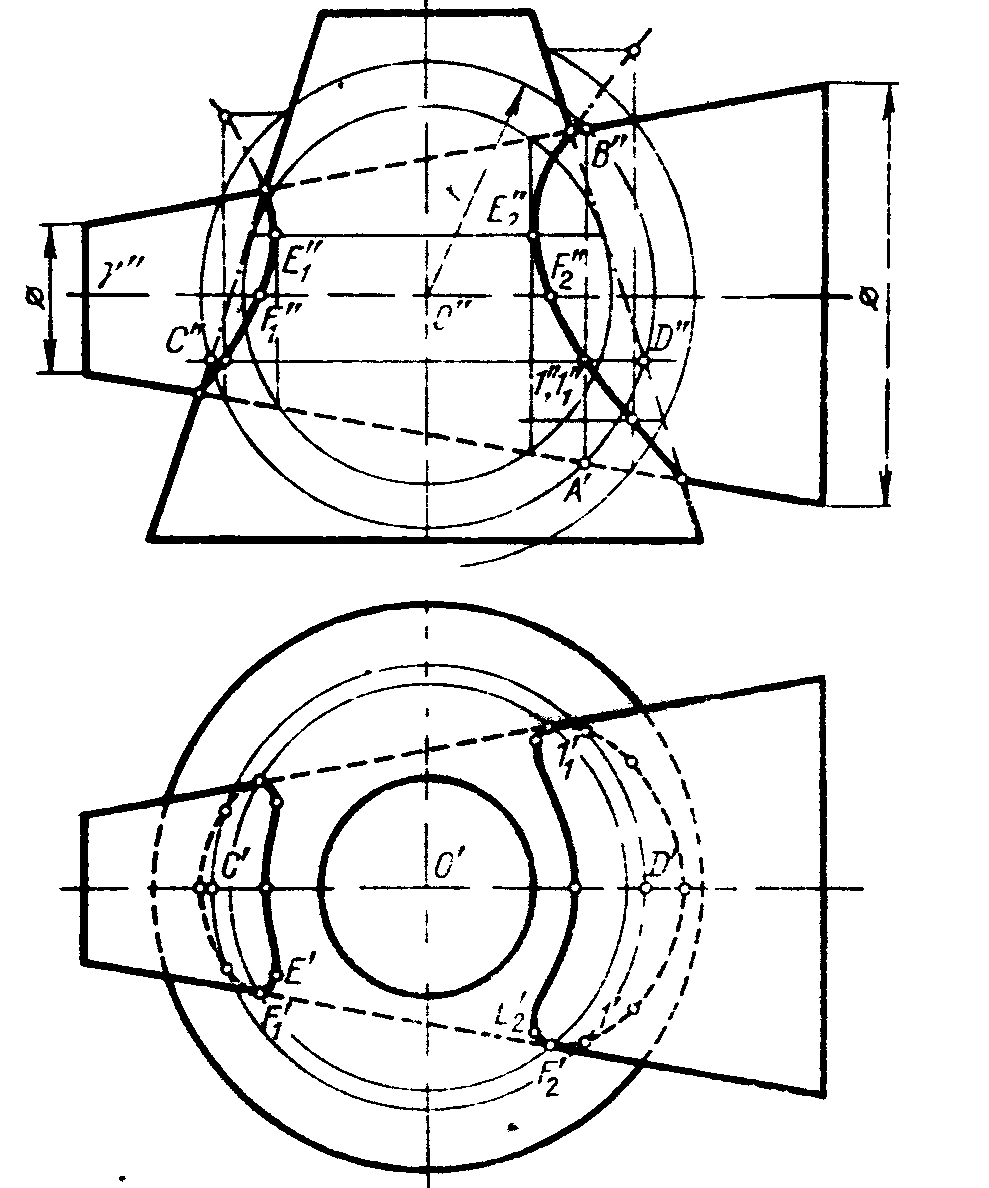
Рис. 10
Линия пересечения, распавшаяся на две части пространственной кривой, из-за наличия у пересекающихся конусов общей плоскости симметрии проецируется на эту плоскость в виде кривой второго порядка, в данном примере – гиперболы.
Ниже приведены примеры частных случаев пересечения поверхностей, основанных на применении теоремы Г. Монжа, имеющей большое практическое применение:
Если две поверхности второго порядка описаны около третьей или вписаны в нее, то они пересекаются по двум плоским кривым. Эти кривые проходят через прямую, соединяющую точки пересечения линий касания.
