3. Давление в водонасыщенных грунтах

Давление, передающееся от сооружения на грунт, распределяется между скелетом грунта и поровой водой. Рассмотрим механическую модель грунтовой массы.

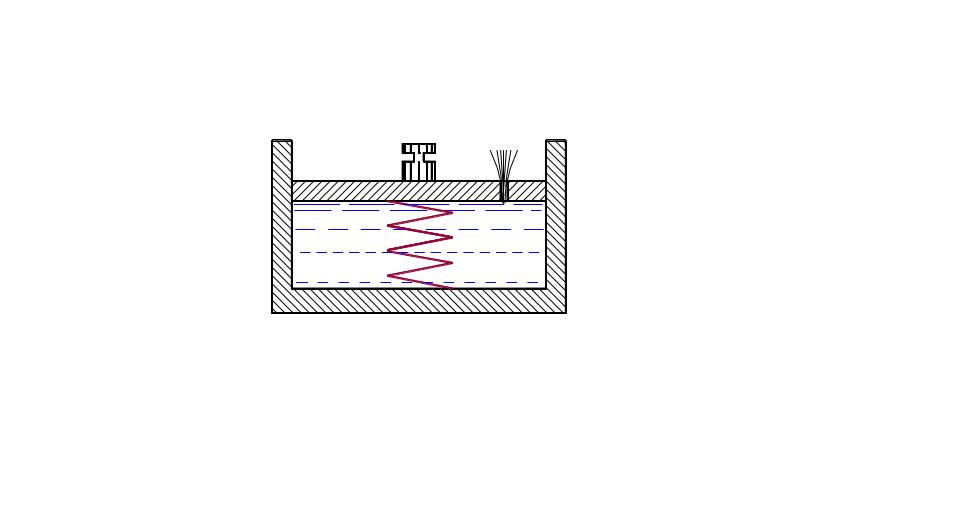
Рис. 2.12. Модель деформации во времени грунта, насыщенного водой

Так как вода несжимаема, в первый момент времени после загружения усилие в пружине будет равно нулю, и вся нагрузка будет восприниматься водой.

По мере выдавливания воды из стакана через отверстие в поршне все большая часть нагрузки будет передаваться на пружину и, следовательно, давление в воде будет уменьшаться, а давление в скелете грунта (отношение усилия в пружине к площади поршня) будет возрастать. При этом в любой момент времени будет сохраняться равенство:

. (2.0)

После выдавливания определенного количества воды из-под поршня давление будет полностью передано на пружину, т.е. при давления в воде и скелете грунта будут соответственно равны и .

Давление в скелете грунта называется эффективным, а давление в поровой воде - нейтральным. Эффективное давление характеризует напряженное состояние скелета грунта, под действием его грунт уплотняется и упрочняется. Нейтральное же давление не уплотняет грунт, а лишь создает напор в воде, вызывающий фильтрация - оно нейтрально по отношению к скелету грунта.

Из формулы ( 2 .0) эффективное давление в любой момент времени равно:

. (2.0)

4. Сопротивление грунтов сдвигу

Грунты в основании сооружений испытывают воздействие не только нормальных, но и касательных напряжений. Когда касательные напряжения по какой-либо поверхности грунта достигают предельного сопротивления, происходит сдвиг одной части массива грунта по другой.

1. Сопротивление сдвигу сыпучих грунтов

Как показывают опыты, сопротивление сдвигу несвязных грунтов происходит за счет сил трения, развивающихся по поверхностям минеральных частиц.

Предельное сопротивление грунтов сдвигу определяют на односрезных приборах.

Цилиндрический образец грунта помещают в срезыватель так, чтобы одна половина оставалась неподвижной, а вторая могла бы перемещаться горизонтально под действием приложенной силы .

Рис. 2.13. Испытание грунта в односрезном приборе

а) схема прибора; б) график сопротивления сдвига сыпучего грунта; в) график сдвигу связного грунта; - угол внутреннего сопротивления трения грунта; - удельное сцепление грунта; - давление связности

К образцу прикладывают переменную сжимающую нагрузку , увеличивая ее ступенями. При каждом значении определяют горизонтальную силу , соответствующую предельному сопротивлению грунта сдвигу и строят график (рис. 2 .13-а). Впервые такие опыты проводил Ш. Кулон в 1773 г. и им было сформулировано предложение, названное позже законом Кулона:

предельное сопротивление сыпучих грунтов сдвигу есть сопротивление трению, прямо пропорциональное нормальному давлению.

Он следует из экспериментальной кривой на рис. 2 .13– б:

, (2.0)

где - коэффициент внутреннего трения; - угол внутреннего трения.

Угол внутреннего трения получил название по аналогии с углом трения для твердых тел:

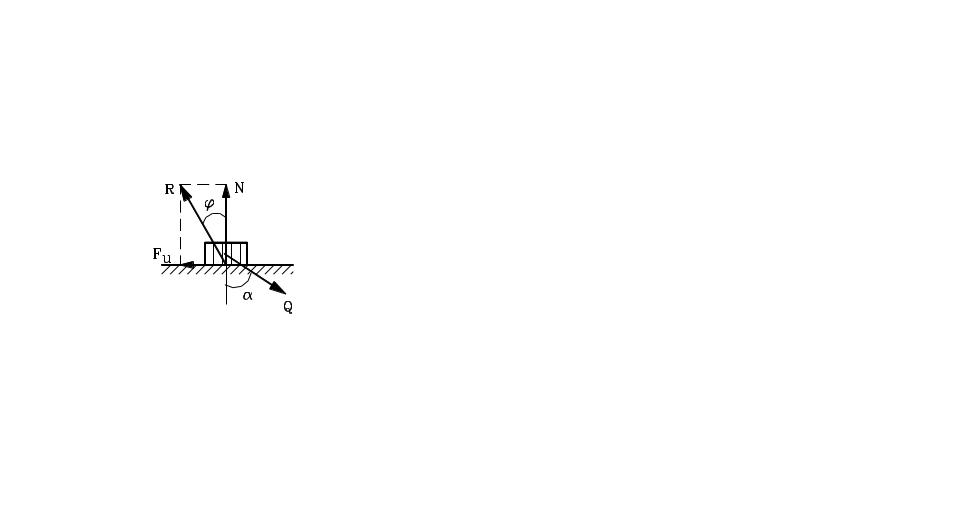
Рис. 2.14. Угол трения у шероховатых тел

- предельная величина силы трения; - внешняя сила; - угол трения.

При изменении силы трения от нуля до максимального значения угол, который составляет реакция с нормалью к опорной поверхности, будет расти от нуля до предельного значения . Наибольший угол, который полная реакция шероховатой связи образует с нормалью к поверхности, называется углом трения . Величина угла трения зависит от шероховатости поверхностей соприкасающихся тел. Для того чтобы тело на шероховатой поверхности могло находиться в равновесии под действием внешней силы , ее линия действия не должна отклонятся от нормали к опорной поверхности более чем на угол ( ).

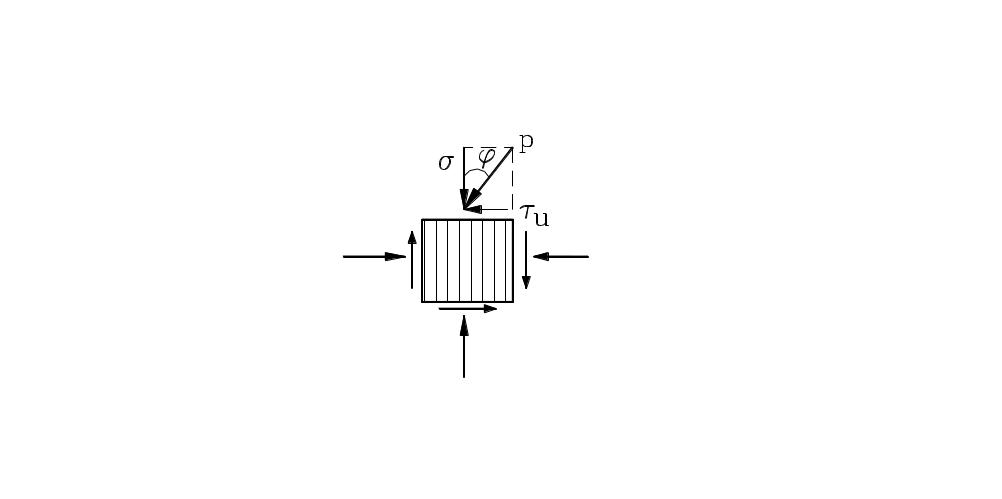
Рис. 2.15. Угол внутреннего трения в грунте

Аналогично, для того, чтобы сдвинулась верхняя часть грунта относительно нижней (рис. 2 .13-a), необходимо, чтобы равнодействующая нормальных и касательных напряжений, действующих по плоскости сдвига (полное напряжение ), составляла с нормалью к этой плоскости угол (Рис. 2 .15). Угол внутреннего трения можно выразить через напряжения и :

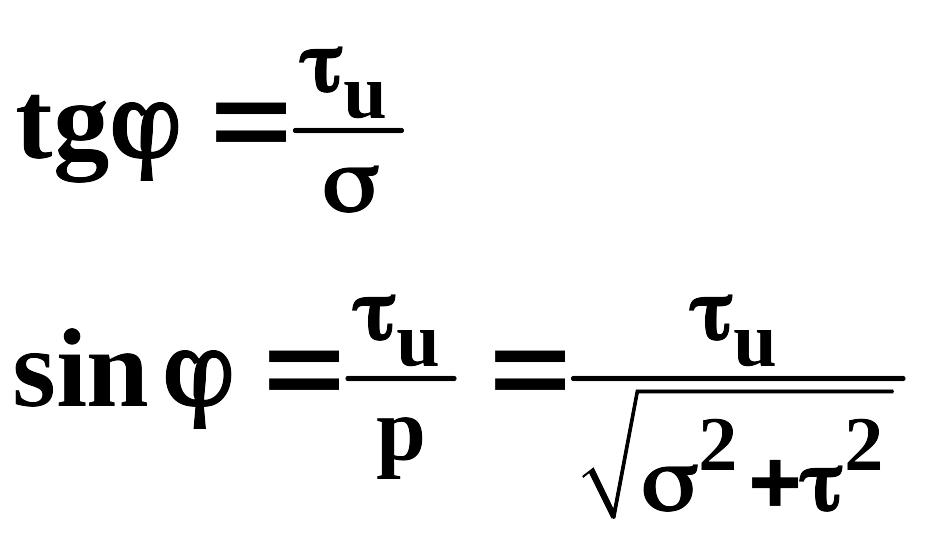. (2.0)