Теоретичні відомості
1 Оцінка випадкових похибок прямих вимірювань
Випадкові похибки проявляються при багаторазових вимірюваннях однієї фізичної величини в однакових умовах одним оператором і за допомогою одного і того самого засобу вимірювання. Такі вимірювання прийнято називати рівноточними.
При статистичній обробці результатів багаторазових вимірювань необхідно виконати таку послідовність дій:
1.Провести
багаторазові вимірювання і отримати
масив
вимірювальної інформації.
2.Поправити результати вимірювань, вилучивши відомі систематичні похибки шляхом внесення поправок у результати вимірювань.
3.Знайти математичне очікування поправлених результатів спостережень і прийняти його за дійсне значення.
Для нормального закону розподілу, а якщо поступитися ефективністю оцінки, то й для всіх симетричних розподілів, за оцінку математичного очікування ряду рівноточних спостережень приймають середнє арифметичне
.
(8)
4.Визначити випадкове відхилення.
Різниця
(9)
є випадковим відхиленням (випадковою абсолютною похибкою) при i-му спостереженні. Вона може бути позитивною і негативною.
Середнє арифметичне незалежно від закону розподілу має такі властивості
і
,
(10)
які
використовуються для перевірки
правильності обчислення
.
5.Обчислити експериментальне середнє квадратичне відхилення (СКВ) результатів вимірювання за формулою Бесселя
,
(11)
де
-
результат i-го вимірювання;
-
середнє арифметичне n результатів.
Підкреслимо,
що для серії
вимірювань однієї й тієї ж величини
параметр
характеризує розсіювання результатів
багаторазових
вимірювань однієї і тієї ж величини.
Оскільки ми обчислюємо середнє
арифметичне, необхідне для одержання
оцінки
,
то природно взяти його за результат
вимірювання. В даному випадку середнє
арифметичне залежить від числа вимірювань
і є випадковою величиною, яка має деякі
дисперсії відносно істинного значення.
6.Визначити середнє квадратичне відхилення середнього арифметичного за формулою
.
(12)
Отже,
якщо в якості результату багаторазових
вимірювань взяти середнє арифметичне
,
то випадкова похибка (
)
зменшується в
раз порівняно з випадком (рис.2),
коли за результат багаторазових
вимірювань приймалось
будь-яке
одне з
n спостережень.
Тому багаторазові вимірювання з наступним усередненням результатів і прийняттям цього середнього за результат вимірювання є досить ефективним методом зменшення випадкової похибки.
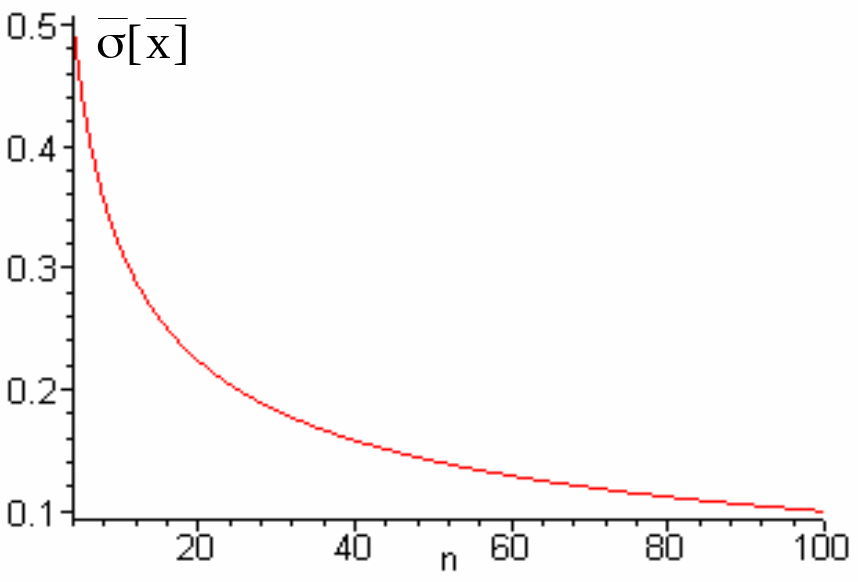
Рисунок 2
7.Визначити довірчі границі похибки вимірювання, що являють собою верхню й нижню межі, які накривають із заданою ймовірністю похибку вимірювання.
Якщо
число вимірювань
,
то довірчий інтервал випадкової похибки
при заданих імовірності Р і середньому
квадратичному відхиленні
визначається
за формулою Стьюдента
,
де
-
коефіцієнт розподілу Стьюдента, який
залежить від заданої ймовірності Р і
числа вимірювань n.
Розглянемо тепер, яку саме довірчу ймовірність необхідно задавати. Як правило, приймають Р = 0.95. Якщо вимірювання повторити неможливо, то Р=0.99, а в особливо відповідальних випадках, коли вимірювання, що виконуються, пов’язані із створенням нових еталонів або їхні результати можуть суттєво вплинути на здоров’я людини, Р = 0.997.
8.Представити результат вимірювання
.
Приклад. Обробка результатів прямих вимірювань.
Проведено ряд вимірювань за допомогою вольтметра магнітоелектричної системи. При цьому одержано такі результати: 122; 118; 120; 121; 119; 120 [В]. Визначити середнє значення виміряної напруги, його СКВ. Представити результат, вказавши границі довірчого інтервалу, в який потрапляє похибка вимірювання із заданою ймовірністю Р=0.95 (коефіцієнт Стьюдента дорівнює 2.571).
1.Знайдемо математичне очікування для ряду вимірювань
.
2.Визначимо випадкові відхилення
3.Перевіримо, чи сума випадкових відхилень дорівнює нулю
.
4.Знайдемо оцінку експериментального середнього квадратичного відхилення
.
5.Визначимо середнє квадратичне відхилення середнього арифметичного
.
6.Знайдемо довірчі границі похибки вимірювання
.
7.Представимо
результат у відповідності до стандартної
форми
.
2 Оцінка випадкових похибок опосередкованих вимірювань
Оцінку випадкових похибок опосередкованих вимірювань необхідно здійснювати за такою методикою:
Визначити для результатів прямих вимірювань і ;
Визначити значення невідомої величини
;Визначити «вагу» кожної часткової похибки опосередкованих вимірювань
;
(1.25)
Обчислити часткові випадкові похибки опосередкованих вимірювань
;
(1.26)
Знайти оцінку СКВ результату опосередкованих вимірювань
;
(1.27)
Знайти (табл.4) коефіцієнт Стьюдента за заданою довірчою ймовірністю Р і кількістю вимірювань n.
Знайти граничні значення випадкової складової похибки, яку приймають за похибку опосередкованого вимірювання
;
8. Записати результат опосередкованого вимірювання:
.
Для визначення похибки результату опосередкованого вимірювання необхідно застосувати такі правила:
1.Якщо результат вимірювання є сумою або різницею двох і більше виміряних величин:
,
і похибки
незалежні і випадкові, то абсолютна
похибка результату може бути визначена
за формулою
.
Коли
похибки аргументів корельовані, значення
може
перевищувати отримане за попередньою
формулою, але завжди буде задовольняти
умову
.
Таблиця 4 - Значення коефіцієнта Стьюдента
-
n-1
P=0.95
Р=0.99
n-1
Р=0.95
Р=0.99
3
3.182
5.841
16
2.120
2.921
4
2.776
4.604
18
2.101
2.878
5
2.571
4.032
20
2.086
2.845
6
2.447
3.707
22
2.074
2.819
7
2.367
3.500
24
2.064
2.797
8
2.306
3.355
26
2.056
2.779
9
2.262
3.250
28
2.048
2.763
10
2.228
3.169
30
2.043
2.750
12
2.179
3.055
14
2.145
2.977
1.960
2.576
2.Якщо кінцевий результат вимірювання є добутком або часткою двох і більше виміряних значень:
,
і похибки
незалежні і випадкові, то відносна
похибка результату опосередкованого
вимірювання визначається
.
3.Якщо результат опосередкованого вимірювання є функцією однієї величини:
,
то похибка результату визначається
.
4.В загальному випадку похибка функції декількох величин
,
похибки яких незалежні і випадкові, знаходиться
,
але сумарна похибка ніколи не перевищить значення
.
Приклад. Обробка результатів опосередкованих вимірювань.
Визначити
результат та СКВ випадкової складової
похибки опосередкованого вимірювання
потужності
за даними прямих вимірювань напруги та
опору з незалежними випадковими
похибками, що розподілені за нормальним
законом:
.
Записати результат згідно зі стандартною формою, вказавши довірчий інтервал, в який потрапить похибка результату опосередкованого вимірювання із встановленою ймовірністю Р=0.99.
Знайти значення математичного очікування потужності
Визначити СКВ результату опосередкованого вимірювання потужності
.
За
значеннями нормованої функції Лапласа
(табл.5) знайти значення z, та визначити
СКВ результатів прямих вимірювань
напруги
і опору
.
Для
Для
Значення СКВ опосередкованого вимірювання потужності складає
.
Визначити границі довірчого інтервалу для заданої ймовірності Р=0.99. Для значення нормованої функції
,
з табл.2
значення
.
Тоді границі довірчого інтервалу становлять
.
Таблиця 5 - Значення нормованої функції Лапласа
-
Z
Ф(z)
Z
Ф(z)
z
Ф(z)
z
Ф(z)
0.0
0.00000
1.0
0.34134
2.0
0.47725
3.0
0.49865
0.1
0.03983
1.1
0.36433
2.1
0.48214
3.1
0.49903
0.2
0.07926
1.2
0.38493
2.2
0.48610
3.2
0.49931
0.3
0.11791
1.3
0.40320
2.3
0.48928
3.3
0.49952
0.4
0.15542
1.4
0.41924
2.4
0.49180
3.4
0.49966
0.5
0.19146
1.5
0.43319
2.5
0.49379
3.5
0.49977
0.6
0.22257
1.6
0.44520
2.6
0.49534
3.6
0.49984
0.7
0.25804
1.7
0.45543
2.7
0.49653
3.7
0.49989
0.8
0.28814
1.8
0.46407
2.8
0.49744
3.8
0.49993
0.9
0.31594
1.9
0.47128
2.9
0.49813
3.9
0.49995
Результат опосередкованого вимірювання потужності
.