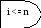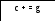Программирование на C / C++ / Лабораторные работы
.doc
Отчет о выполнении лабораторных работ по дисциплине
«Алгоритмические языки в вычислительной технике»
Алгоритм №1: Калькулятор
Цель: Произвести программное сложение двух произвольных чисел
Состав интерфейса: Два поля ввода, одна кнопка, одна надпись
В поля ввода пользователь вводит два произвольных целых числа.
Сложение происходит при нажатий на кнопку. При этом срабатывает функция TForm1::Button1Click
Ниже приводится ее листинг:
int a = StrToInt(Edit1->Text); //1
int b = StrToInt(Edit2->Text); //2
// a и b - слогаемые
int c = a + b; // 3 Переменная с – результат сложения переменных a и b
4 Label1->Caption = IntToStr(c); //4 Вывод результата в надпись
В строках 1 и 2 происходит объявление целочисленных переменных и присвоение им чисел-слогаемых с помощью функции StrToInt(), которая возвращает число, взятое из строковой переменной.
В строке 3 объявляется переменная с и она принимает результат функции a + b, то есть сумму слогаемых
В строке 4 происходит обратное преобразование числа с в строковую форму и вывод его в надпись.
Вывод: Данный программный код способен получать вводимые пользователем числа и представлять их сумму как результат своей работы.
Алгоритм №2: Применение формулы Тейлора для вычисления алгебраических функций
Цель: Вычислить арифметическими методами приближенное значении алгебраической функции Экспонента
Состав интерфейса: Одно поле ввода, одна надпись, одна кнопка
Процессор ЭВМ не способен вычислять алгебраические функции, такие как экспонента, синус, косинус, но есть методы, позволяющие вычислить их путем вычисления множества арифметических операций.
Одним из таких методов является метод Тейлора-Маклорена. Он заключается в представлений функций в виде суммы членов
![]()
Таким методом несложно произвести программное вычисление.
В поле ввода пользователь вводит аргумент, затем он нажимает на кнопку, код которой представлен в листинге
float x = StrToFloat(Edit1->Text); /* Присвоение переменной аргумента в виде числа с плавающей точкой */
float a = 0; // Эта переменная получит конечный результат
float r = 1; // Эта переменная будет содержать последующий член многочлена
for(int i = 1; i<10; i++){ // Организация цикла из десяти шагов
a = a + r; // Прибавление нового члена
r = r * x / i; // Вычисление последующего члена
}
Label1->Caption = FloatToStr(a); // Вывод результата
При этом в процессе работы нет необходимости возводить какое-либо число в степень или вычислять его факториал. На каждом витке цикла переменная r сохраняет в себе значение предыдущего члена, и будучи умноженной на соотношение x / i получает новый член
Вывод: Данный алгоритм способен арифметическими методами вычислять экспоненту произвольного числа
Алгоритм №3: Программная обработка ошибок
Цель: Научиться отлавливать и обрабатывать ошибки во время выполнения программного кода
Состав интерфейса: Два поля ввода, одна кнопка, одна надпись
Рассмотрим пример программного вычисления силы тока по закону Ома
Формула I = U / R записывается в виде программного кода. В два поля ввода пользователь вписывает известные напряжение и сопротивление. Затем следует нажатие на кнопку, которое и приводит в действие механизм вычисления.
Теперь представим, что в поле для ввода значения сопротивления введен ноль. Программа, тем не менее, выполнит код, но на этапе деления произойдет ошибка, которая, будучи необработанной, приведет к завершению работы программы. Для нас целесообразно предотвратить завершение работы и сообщить пользователю о сбое.
Листинг кода кнопки:
float u =StrToFloat(Edit1->Text); // (1) Получение значения напряжения
float r = StrToFloat(Edit2->Text); // (2) Получение значение сопротивления
if(r<0){ //(3)
ShowMessage("Сопротивление должно быть больше нуля!”); //(4)
return; //(5)
} //(6)
try{ //(7)
float i= u/r; //(8)
Edit3->Text = FloatToStr(i); //(9)
} //(10)
catch(EZeroDivide &e){ //(11)
ShowMessage("Сопротивление должно быть больше нуля!"); //(12)
} //(13)
В строках 7 – 13 работает система отлова ошибок try – catch. По умолчанию работает код внутри оператора try. Если в этом коде возникает ошибка, то срабатывает код оператора catch. При этом тип переменной EZeroDivide как раз таки и свидетельствует о том, что произошло деление на ноль.
В строке 12 пользователь получает сообщение о том, что произошло деление на ноль. Программа продолжает свою работу.
В строках 3 – 6 происходит проверка значения сопротивления на неотрицательность
Сопротивление в проводнике при любых условиях не может быть отрицательным. Но компьютер об этом не знает. Поэтому с помощью оператора if() производится проверка, и если сопротивление отрицательно, то пользователю выводится уведомление и дальнейший программный код не выполняется.
Вывод: Данной программный код защищен от возможных ошибок выполнения программы.
Алгоритм №4: Применение оператора break
Цель: Разработать алгоритм, способный прерывать работу цикла с помощью оператора break
Состав интерфейса: Два поля ввода, кнопка
Предположим нам нужно произвести сложение одного и того же числа n раз, причем условие таково, что количество сложении должно быть более двух (n > 2)
В первое поле ввода пользователь вводит само число, а во второе количество сложений.
Затем он нажимает кнопку и происходит сложение.
Листинг события нажатия первой кнопки:
float g = StrToFloat(Edit1->Text); //(1)
int n = StrToInt(Edit2->Text); //(2)
float c=0; //(3)
for(int i=1;i<=n;i++){ //(4)
if(n<=2){ //(5)
ShowMessage("Количество сложений должно быть больше 2!"); //(6)
break; //(7)
} //(8)
c+=g; //(9)
} //(10)
ShowMessage(FloatToStr(c)) //(11)
Данная подпрограмма получает слогаемое в переменную g и количество сложений в переменную n. Переменная c получит конечный результат на выходе из цикла.
В строках (5)-(8) происходит проверка количества сложений, и если оно не больше 2, то происходит остановка цикла оператором break. В противном случае по команде строки (11) пользователь узнает результат сложения из сообщения.
Вывод: Данный программный код содержит цикл, способный прекращать работу с помощью оператора break
Алгоритм №5: Применение оператора continue
Состав интерфейса: Два поля ввода, один список, одна кнопка
Цель: Разработать цикл, способный пропускать шаг при определенных условиях
Рассмотрим пример, когда имеются два числа, и стоит задача получить все чётные числа, заключенные в промежутке исходных двух.
В два текстовых поля пользователь вводит меньшее и большее числа.
По нажатию на кнопку срабатывает следующая подпрограмма:
int a=StrToInt(Edit1->Text); //(1)
int b=StrToInt(Edit2->Text); //(2)
float x; //(3)
int y; //(4)
for(int i=a;i<=b;i++){ //(5)
x = i / 2; //(6)
y = (int) x; //(7)
y = y * 2; //(8)
if(y != i){ continue; } //(9)
ListBox1->Items->Add(IntToStr(i)); //(10)
} //(11)
Переменные а и b получают исходные целые числа. Организуется цикл от a до b.
Внутри цикла происходит проверка четности числа. Число делится на два, затем если у него остается дробная часть, то она отбрасывается путем преобразования числа из типа данных float в int. Полученное число вновь умножается на два. Если полученный результат соответствует проверяемому числу, то он вносится в список командой строки (10). Иначе в строке (9) происходит переход к следующему шагу цикла командой continue
Вывод: Данный алгоритм способен пропускать шаг цикла при определенных условиях.
Блок-схема алгоритма №1 Блок-схема алгоритма №2
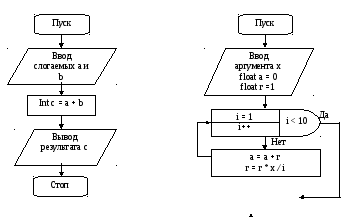



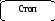
Блок-схема алгоритма №3

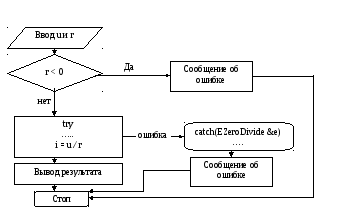

Блок-схема алгоритма №4 Блок-схема алгоритма №5

Нет
Нет
Да
Нет
i = 1
i++
Да
Нет
Да
Да