Лекция 7.

Магнитное поле проводника с током и магнитное поле постоянных магнитов. Сила Лоренца и определение магнитной индукции. Закон преобразования магнитного поля, магнитное поле движущегося точечного заряда, закон Био-Савара-Лапласа. Сила, действующая на проводник с током, закон Ампера, сила взаимодействия между проводниками с током, единицы измерения заряда, тока, индукции.

Опыт показывает, что на покоящийся заряд вблизи нейтрального проводника с током в сила не действует. Но если заряд движется относительно проводника, то в общем случае на него действует сила. То есть проводник с током оказывает силовой действие на движущийся заряд. Этот опытный факт служит для введения особого физического объекта, магнитного поля, порождаемого движущимися зарядами (током). В свою очередь магнитное поле проявляется силовым действием на движущиеся заряды. Источником магнитного поля могут быть и особые вещества – постоянные магниты. Именно они были первыми источниками магнитного поля. Но, как мы узнаем впоследствии, магнитное поле может создаваться только движущимися электрическими зарядами; никаких магнитных зарядов не существует. В постоянных магнитах существуют замкнутые токи, которые и порождают магнитное поле.

Совокупность экспериментальных данных по ислледованию силового действия магнитного поля сводится к следующим фактам.

1. Существует выделенное направление, при движении вдоль которого сила равна нулю.

2. Сила пропорциональна заряду частицы и пропорциональна перпендикулярной составляющей скорости к выделенному направлению.

3. При равных зарядах и скоростях сила зависит от силы тока, конфигурации проводиков, положения частицы относительно проводников.

Все эти факты можно объединить следующей формулой

(1)

Здесь - величина заряда, см/сек числовой коэффициент (вводится из соображений удобства), - скорость заряда, - некоторый вектор, величина и направление которого зависит от проводника и тока. При движении вдоль этого вектора сила равна нулю, а при движении перпендикулярно сила максимальна. Сила, описываемая выражением (1), называется силой Лоренца. Этот вектор и называется индукцией магнитного поля. Для его измерения необходимо: (1) определить направление, при движении вдоль которого сила обращается в нуль, (2) запустить частицу со скоростью в перпендикулярном направлении.Тогда индукция магнитного поля определяется формулой

(2)

Индукция для магнитного поля играет такую же роль как напряженность для электрического поля.

Итак, основанием для введения понятия магнитного поля является сила Лоренца. Иногда, силой Лоренца называют следующее выражение

(3)

Источником магнитного поля могут быть только движущиеся электрические заряды. Опыт показывает, что движущийся точечный электрический заряд порождает в окружающем пространстве магнитное поле с индукцией, даваемой выражением

(4)

Здесь радиус-вектор от заряда в точку наблюдения, напряженность электрического поля точечного заряда (знак штрих означает, что это поле в системе отсчета, связанной с зарядом. Источником этой формулы можно считать опыт. Но ее можно вывести и теоретически, если использовать закон Кулона, инвариантность (независимость от движения) заряда и преобразования Лоренца, с которыми мы познакомимся в последующем курсе классической электродинамики.

На основе формул (3,4) можно исследовать вопрос преобразовании магнитного поля при переходе от одной инерциальной системы к другой. Действительно, если источником магнитного поля служат движущиеся заряды, то в одной системе отсчета магнитное поле будет, а в другой, в которой заряды покоятся, магнитное поле должно быть равно нулю. Пусть система движется относительно системы со скоростью . Тогда для скоростей имеем

Силы должны быть равны (ускорения равны и массы равны):

Если в движущейся системе магнитного поля нет ( ), тогда

(5)

С другой стороны для магнитного поля из (4) имеем (для малых скоростей ):

(6)

Если мы имеем не один движущийся заряд, а множество движущихся зарядов, которые создают плотность тока , то прямым суммированием в формуле (4) получаем выражения

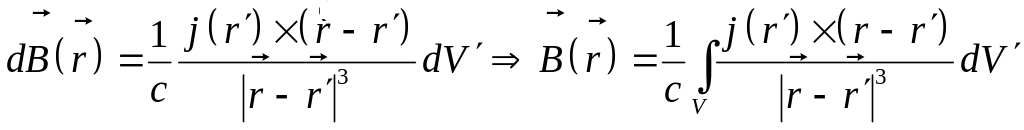(7)

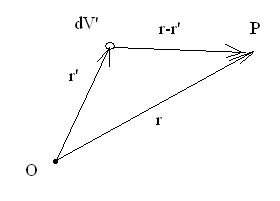
Здесь - радиус-векторы точки наблюдения и малого объема с током. Формула (7) носит название закона Био-Савара-Лапласа. Она позволяет рассчитать индукцию произвольного распределения токов. В тех случаях, когда ток не распределен по объему, а локализован в проводах,можно использовать следующую замену

где - элемент длины вдоль линии тока. С этой заменой закон Био-Савара-Лапласа принимает следующую форму

(8)

Аналогичную формулу можно написать и для поверхностно распределенных токов

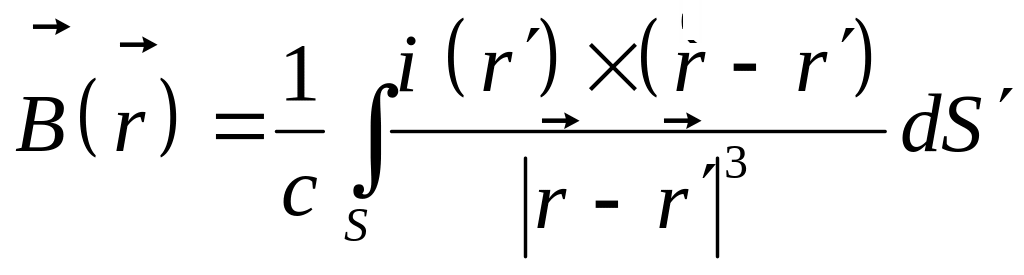(9)

Выражение для силы Лоренца позволяет рассчитать силу на элемент провода с током. Рассмотрим часть провода с объемом и просуммируем выражение (1) по всем движущимся зарядам в этом объеме. В результате получим для силы на этот элемент провода с током выражение

(10)

Здесь , - длина выбранной части проводника, -единичный вектор вдоль проводника в направлении тока, - величина тока в проводнике. Чтобы подсчитать полную силу надо взять интеграл по всему проводнику

(11)

Формулы (10,11) выражают закон Ампера, который дает силу действующую напроводник с током. Если объединить закон БСЛ и закон Ампера, то получим закон, описывающий взаимодействие двух проводников с током

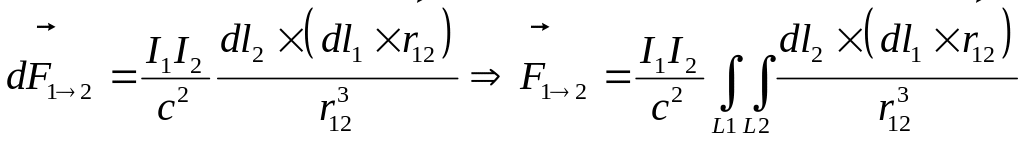(12)

Здесь радиус-вектор от элемента к элементу . Отметим, что в общем случае сила со стороны проводника 2 на проводник 1 отличается от силы сос тороны проводника 1 на проводник 2:

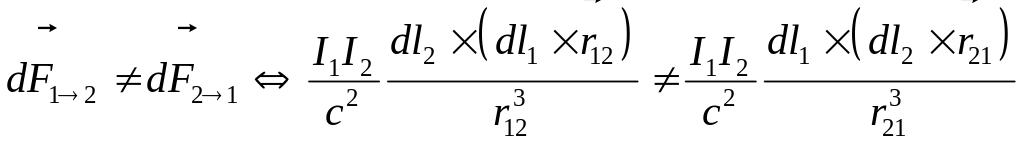(13)

Теперь мы подробно остановимся на выборе единиц измерения заряда, тока и индукции. Ранее, при рассмотрении закона Кулона, мы выбрали за единицу измерения заряда . Напомним, что такой заряд взаимодействует с равным ему зарядом, находящимся на расстоянии с силой в :

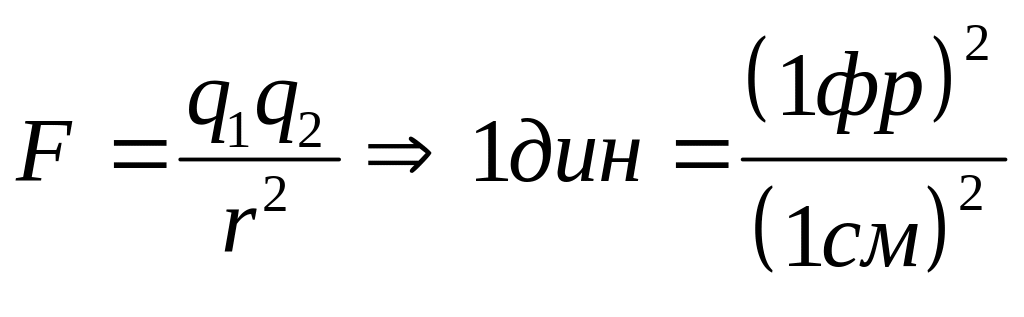(14)

То есть закон Кулона был выбран определяющим для введения единиц заряда. По этой причине все формулы электростатики выглядят максимально просто в этой системе единиц (система ). Аналогичный подход может быть использован при изучении магнетизма. Рассмотрим два параллельных, единичных элемента с токами разделенных расстоянием . Из формулы (13) имеем

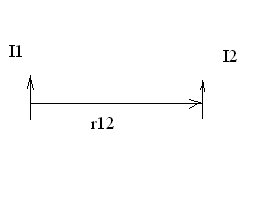
(15)

Естественно выбрать за единицу тока, , такой ток, который взаимодействует с равным током, находящимся на расстоянии , с силой в . Из формулы (15) следует, что

Соответственно, для единиц заряда получаем соотношение

В системе единиц СИ единицей заряда является величина , а единицей тока (ампер). Теперь мы можем определить единицу измерения индукции магнитного поля. Если измерять заряд в системе , то формула для силы Лоренца примет вид

(16)

Приняв это выражение за определяющее, мы выбираем за единицу измерения индукции магнитного поля : в поле с такой индукцией на заряд в , движущийся со скоростью в направлении, перпендикулярном к направлению индукции, действует сила равная . Заметим, что в системе единиц формулы для силы Лоренца, законов Био-Савара-Лапласа, Ампера пишутся без множителя . Иногда мы будем использовать эту систему, но чаще мы будем использовать для заряда, тока единицы , а индукцию измерять в гауссах (соответственно, в указанных выше формулах следует сохранить множитель ). Итак, еще раз:

Сначала определяют 1 СГСМ ед.тока как такой ток, при котором два параллельных проводника с током на расстоянии 1см взаимодействуют с силой в 1дину. Эта единица равна . Затем определяют .

Индукцию магнитного поля измеряют в Гс (гауссах). По определению, магнитное поля с индукцией в действует на заряд величиной , движущийся со скоростью в перпендикулярном к индукции направлении, с силой в .

Лекция 8.

Векторный потенциал, его выражение через плотность тока, теорема Гаусса для индукции магнитного поля. Теорема о циркуляции для индукции магнитного поля. Потенциальные и соленоидальные поля. Элементарный виток с током (магнитный диполь), энергия магнитного диполя во внешнем поля и сила, действующая на магнитный диполь в магнитном поле. Поле магнитного диполя.

Расчеты индукции магнитного поля могут быть значительно упрощены путем введения вспомогательного вектора, который называется векторным потенциалом

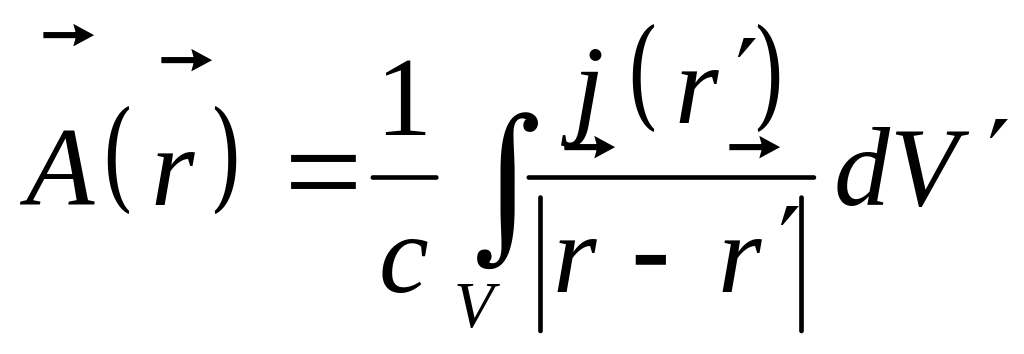(1)

Чтобы оценить полезность введения векторного потенциала, возьмем ротор от выражения (1). Заметим, что дифференцирование при взятии роторы идет по нештрихованным координатам, а интегрирование по штрихованным. Поэтому операцию ротор можно внесте под знак интеграла:

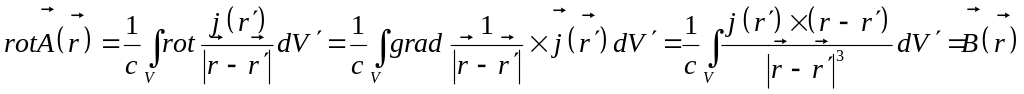
При этом мы использовали формулы векторного анализа

(2)

Итак, индукция магнитного поля выражается через вспомогательный вектор формулой

(3)

Иногда оказывается более удобным вместо прямого использования закона Био-Савара-Лапласа сначала вычислить векторный потенциал, а затем взять от него ротор и получить индукцию магнитного поля.

Полезность векторного потенциала этим не исчерпывается. Он оказывается очень полезным для получения общих теорем относительно свойств индукции магнитного поля. Действительно, взяв дивергенцию от соотношения (3), мы немедленно получаем утверждение (так как дивергенция ротора равна нулю)

(4)

Это утверждение носит название дифференциальной формы теоремы Гаусса для индукции магнитного поля. Получим интегральную форму этого утверждения. Для этого проинтегрируем уравнение (4) по произвольному объему и воспользуемся теоремой Остроградского-Гаусса, которая связывает и нтеграл по объему с интегралом по поверхности этого объема:

(5)

то есть поток индукции по любой замкнутой поверхности равен нулю. Сравним теорему Гаусса для индукции магнитного поля с соответствующей теоремой для напряженности электрического поля

(6)

Это сравнения можно интерпретировать как отсутствие в природе магнитных (смотри замечание в начале лекции 7). Структуру магнитного поля (также и электрического поля )удобно изображать с помощью магнитных силовых линий: кривые, касательные к оторым в каждой точке пространства совпадают снаправлением вектора (обсудить как выбрать одно из двух возможных направлений силовой линии). На языке силовых линий утверждение теоремы Гаусса для магнитного поля сводится к утверждению, что магнитные силовые линии не имеют начала и конца, а являются замкнутыми.

Получим теперь теорему о циркуляции индукции магнитного поля по замкнутому контуру. Для этого вычислим ротор индукции магнитного поля:

(7)

Здесь использована известная формула векторного анализа , и лапласиан равен . Позже мы покажем, что всегда можно положить . Тогда формуы (7,1) дают

(8)

То есть мы получили утверждение

(9)

Это утверждение называется дифференциальной формой теоремы о циркуляции для индукции магнитного поля. При этом иы использовали два математических результата

(10)

Первое утверждение может быть проверено непосредственным вычислением (с учетом свойств - функции). Кроме того, его справедливость можно увидеть из анализа решения для потенциала точечного заряда

(11)

Второе утверждение в (10) является фактически определение обобщенной - функции. Можно получить и интегральную форму теоремы о циркуляции. Для этого рассмотрим произвольный (достаточно гладкий контур) и поверхность, которая опирается на этот контур

Вычислим поток через поверхность и воспользуемся теоремой Стокса (поток от ротора вектора преобразуется в циркуляцию вектора):

(12)

Покажите, что правая часть в (12) не зависит от выбора поверхности (при фиксированном контуре).

Доказанные теоремы позволяют дастаточно просто решать задачи с простой геометрией токов. Рассмотрим, например, вычисление индукции для бесконечного прямого провода с током

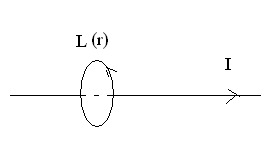
Индукия направлена по касательной к выбранному круговому контуру радиуса и в силу симметрии одинакова для любой точки контура. Отсюда циркуляция равна

(13)

Аналогично рассматриваются другие простые задачи (например, индукция магнитного поля бесконечного соленоида).

Сравним теперь теоремы Гаусса и о циркуляции для электрического и магнитного полей:

(14)

(15)

Векторное поле со свойствами (14) (ротор равен нулю) называется потенциальным или безвихревым. Для такого поля циркуляция по любому замкнутому контуру равна нулю, то есть силовые линии не образуют вихрей. Векторное поле со свойствами (15) состоит только из вихрей: оно называется вихревым или соленоидальным.

Рассмотрим некоторую ограниченную область, в которой текут замкнутые токи и вычислим векторный потенциал на больших (много больших, чем размер области) расстояниях. То есть нам надо приближенно вычислить

(16)

Подобную задачу мы решали для электрического потенциала при рассмотрении дипольного приближения. Также как и там используем разложение

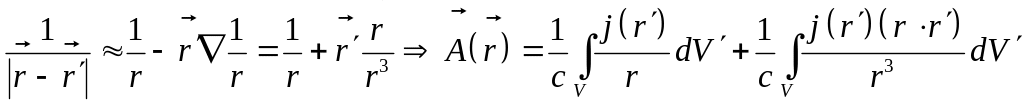(17)

Первый интеграл в (17) равен нулю (разбиваем область на трубки с током, которые замкнуты):

Преобразуем второй интеграл следующим образом

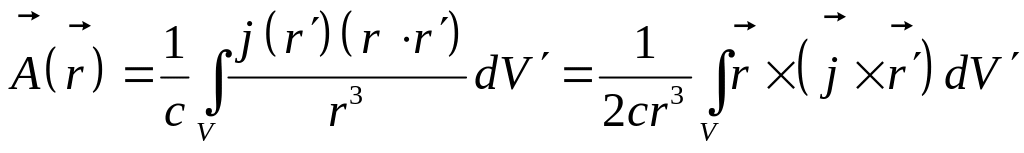(18)

Довольно трудное, но короткое доказательство приведено в приложении к этой лекции.

Определим магнитный момент области с токами как

(19)

Тогда векторный потенциал на больших расстояних с учетом (18) равен

(20)

Можно вычислить и индукцию

(21)

В чем-то формулы (20,21) напоминают формулы для потенциала и напряженности электрического поля элементарного диполя. Формулу (19) для маленького витка с током можно записать так

(22)

Где площадь витка с током, - ток, - единичный вектор, определяемый по правилу правого винта. Вычислим потенциальную энергию витка с током в постоянном магнитном поле. Рассмотрим процесс образования (растягивания витка от нулевой площади). При перемещении контура с током совершается работа

Это работа силы Ампера, а работа против силы Ампера как раз и равна потенциальной энергии

(23)

Это выражение совпадает с энергией электрического диполя в однородном электрическом поле. Отсюда следует, что и вращающий момент для магнитного диполя должен даваться формулой, аналогичной формуле для электрического диполя

(24)

Приложение.

Симметричная часть дает нуль после перехода к поверхностному интегралу.

Антисимметричная часть дает компоненту двойного векторного произведения

Лекция 9.

Электрические и магнитные поля в веществе. Намагниченность и напряженность магнитного поля, смысл вектора напряженности магнитного поля. Магнитная восприимчивость и магнитная проницаемость вещества. Механизмы намагничивания: диа, пара и ферромагнетики. Единицы измерения напряженности. Теорема о циркуляции для напряженности магнитного поля. Граничные условия на границе раздела двух магнетиков.

Мы уже использовали понятие электрического поля в веществе при изучении диэлектриков и проводников. Так в соотношениях

фигурирует напряженность электрического поля в веществе. На самом деле мы недостаточно подробно обсудили это понятие и закрыли глаза на очень важную проблему. Делов том, что любое вещество состоит из атомов (положительно заряженные ядра и отрицательно заряженные электроны), ионов различных знаков, которые создают быстро меняющиеся с расстоянием электрическое поле в веществе. Быстро – означает, что даже на расстояниях порядка размера атома или межатомных расстояниях электрическое поле меняется очень сильно (на величину сравнимую со своим значением). Назовем истинное электрическое поле, создаваемое всеми зарядами, микроскопическим полем. Его пространственную зависимость схематично можно изобразить так (рисунок 1а):

Рис.1.

На плавное изменение в пространстве наложена быстрая и значитеьная рябь. Зависимость микроскопического поля от расстояния очень сложная, она содержит два масштаба: длину l - расстояние быстрых изменений (порядка ширину зубцов), длину L – расстояние медленных изменений (длин, на которой меняется кривая b). Если функцию, изображенную на рисунке 1а усреднить по отрезкам , то из кривой a, получится кривая b. Порцедура усреднения заключается в следующем

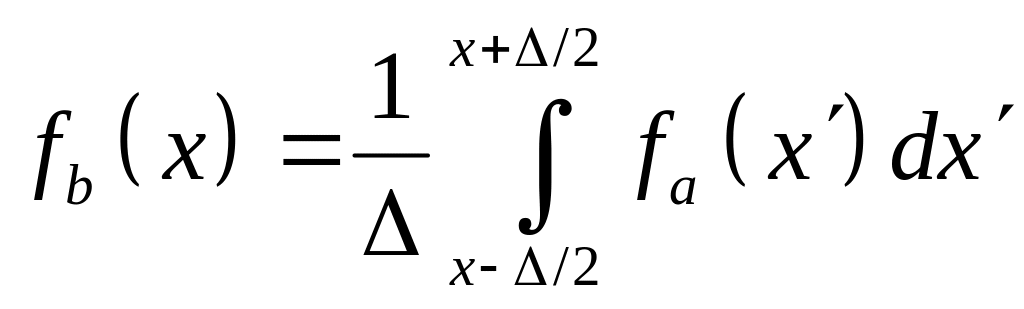
При рассмотрении электрического поля в веществе производят аналогичное (только трехмерное) усреднение:

(1)

Интнегрирование здесь идет по физически бесконечно малому объему около точки . Физически бесконечно малый объем много больше области микроизменений (масштаба ), но много меньше области макроизменений (масштаба ). Именно это усредненное поле и рассмаривается как электрическое поле в веществе. Уравнения для усредненного поля в электростатике получаются усреднением уравнений для микроскопического поля следующим образом:

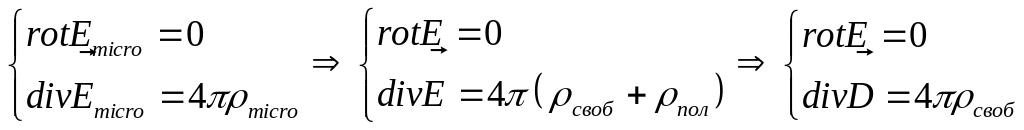(2)

Где величины без индексы являются усредненными. Мы получили обычные уравнения с заменой истинных величин усредненными.

Магнитное поле создается только токами, которые можно разделить на два вида: макроскопические токи и микроскопические (или молекулярные токи: движение электронов в атомах, спин электронов). Истинная или микроскопическая индукция создается всеми токами и очень быстро меняется в пространстве. Проведем процедур усреднения, аналогичную (2):

(3)

Используем теперь понятие магнитного момента, введенное на прошлой лекции. Дело в том, что молекулярные токи представляют собой замкутые токи микроскопического размера. Естественно рассматривать их как совокупность элементарных магнитных диполей. Введем плотность магнитного момента или намагниченность (магнитный момент единицы объема):

(4)

Последнее выражение есть магнитный момент молекулярных токов в объеме . Их вклад в векторный потенциал равен (формула (20) предыдущей лекции):

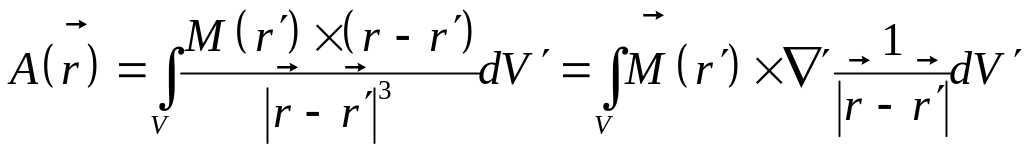(5)

Далее используем формулу

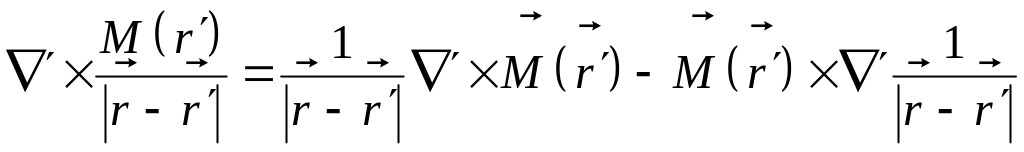
Подставив ее в (5), получим

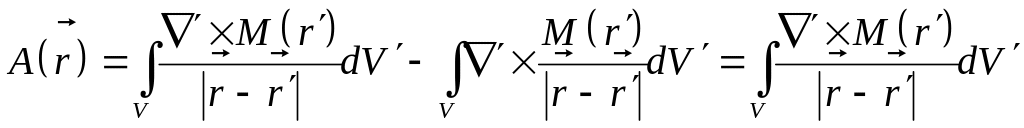(6)

Так как интеграл 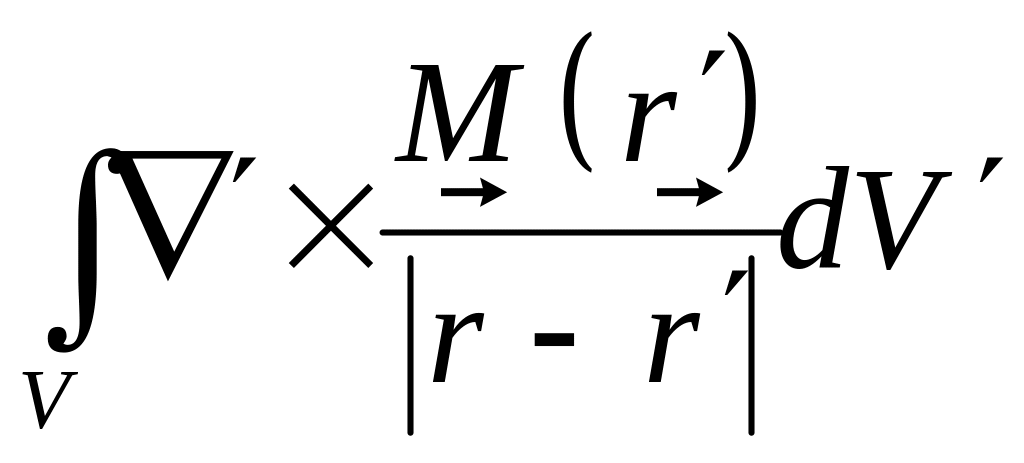равен нулю (одна из теорем векторного анализа аналогичная теорема ОГ). С другой строны для вклада молекулярных токов можно было сразу написать выраже ние

(7)

Сравнение (6,7) дает

(8)

Подставим это в систему уравнений (3)

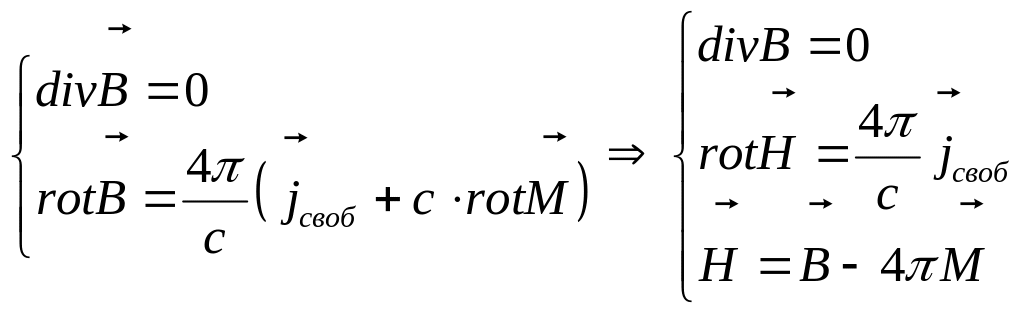(9)

Величина называется напряженностью магнитного поля. Она определяется только свободными (макроскопическими) токами. По смыслу она аналогична индукции электрического поля (которая определяется свободными зарядами). С другой стороны силовая характеристика магнитного поля (индукция) аналогична напряженности электрического поля. Такие названия сложились исторически и часто служат источником распространенной ошибки. Очевидно, что и индукция, и напряженнсть магнитного поля имеют одинаковую размерность. Поэтому они должны измеряться в одинаковых единицах (гауссах). Однако, также по историческим причинам, напряженность измеряют в гауссах, но приэтом называют гаусс эрстедом (последнее также часто служит источником ошибок).

Уравнение

(10)

называется дифференциальной формой теоремы Гаусса для напряженности магнитного поля. Ей можно, стандартным образом, придать интегральную форму

(11)

Смысл введения вспомогательного понятия напряженности состоит в том, что она определяется только свободными токами и не зависит молекулярных токов, которые часто неизвестны.

Для малых полей и достаточно симметричных тела намагниченность связана с напряженностью магнитного поля линейным соотношением

(12)

Величина называется магнитной восприимчивостью. С учетом уравнения (9) получаем

(13)

Величина называется магнитной проницаемостью.

С точки зрения магнитных свойств можно выделить три больших класса веществ: диамагнетики ( чуть меньше 1), парамагнетики ( чуть больше 1), ферромагнетики ( ). Как уже отмечалось, магнитные свойства вещества обусловлены внутренними микроскопическими токами (движением электронов по замкнутым орбитам или спином электронов). В диамагнетиках все внутренние токи скомпенсированы и в отсутствие внешнего поля создавемый ими магнитный момент равен нулю. Приложение внешнего поля вызывает такое изменение движения электронов, что возникающие токи создают магнитный момент ослабляющий внешнее приложенное поле. Диамагнетиками, например, являются простые металлы с заполненными электронными оболочками (медь). В парамагнетиках молекулы (атомы, электроны) изначально имеют магнитные моменты, которые без внешнего поля ориентироованы хаотично. Поэтому полный магнитный момент равен нулю. В приложенном магнитном поле магнитным моментам энергетически более выгодно быть ориентированным по полю. Это приводит к возникновению отличного от нуля полного момента (намагниченности). Можно сказать, то в диамагнетиках , а в парамагнетиках , но в обоих случаях . В ферромагнетиках между магнитными моментами молекул существует взаимодействие, которое делает энергетически более выгодным параллельную взаимную ориентацию. В результате, исходно в ферромагнетике существует спонтанный и очень большой магнитный момент. Внешнее поле просто ориентирует спонтанный момент параллельно самому себе, и возникает результирующее поле много большее, чем приложенное. В ферромагнетиках существуют эффекты памяти (зависимости от предистории). Так намагниченность как функция приложенного поля имеет следующий вид (петля гистерезиса, схематично):

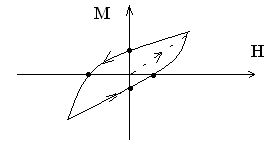
Рис.2.

Рассмотрим теперь вопрос теореме Гаусса для напряженности магнитного поля. Можем ли мы утверждат, что

В силу равенств вопрос сводится к следующему: можно ли создать такую намагниченность, чтобы ? Нетрудно придумать такую конфигурацию микротоков. Возьмем правильный тетраэдр, на каждую грань поместим круговой ток так, чтобы магнитный момент был направлен внутрь тетраэдра. Тогда имеем

Области с таким свойством можно считать областями с эффективным магнитным зарядом (хотя истинного магнитного заряда нет). Интересно, что объекты такого типа действительно существуют в природе.

Наконец, рассмотрим вопрос о граничных условиях на границе двух магнетиков.

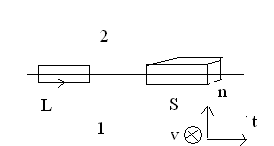
Рис.3.

Выбирая поверхность как показано на рисунке и используя теорему Гаусса для индукции, получаем условие

(14)

Для тангенциальных составляющих соотношение получается при выборе контура и использовании теоремы о циркуляции для напряженности магнитного поля

(15)

где единичные вектора - образуют правую тройку и изображены на рисунке.

Лекция 10.

Закон электромагнитной индукции и уравнение для вихревого электрического поля. Взаимная энергия контуров с током, энергия магнитного поля. Ток смещения. Дифференциальные и интегральные формы уравнений Максвелла. Закон сохранения заряда.

В 1831 году Фарадей сделал одно из самых фундаментальных открытий в электродинамике: он открыл явлений электромагнитной индукции. Суть явления состоит в следующем. Возьмем катушку, концы которой соединим с гальванометром. При приближении к катушке магнита в цепи возникает индукционный ток и стрелка гальванометра отклоняется. При удалении магнита стрелка отклоняется в противоположную сторону. Аналогично, направление тока меняется, если магнит повернуть на . Если двигать катушку, оставляя магнит неподвижным, то стрелка гальванометра также отклоняется. Все это означает, что в контуре с гальванометром появляется ЭДС.

Понять происхождение ЭДС позволяет следующий простой (и схематичный) эксперимент. Рассмотрим конфигурацию проводников изображенных на рисунке 1(пунктирными стрелками показано положительное направление обхода контура):

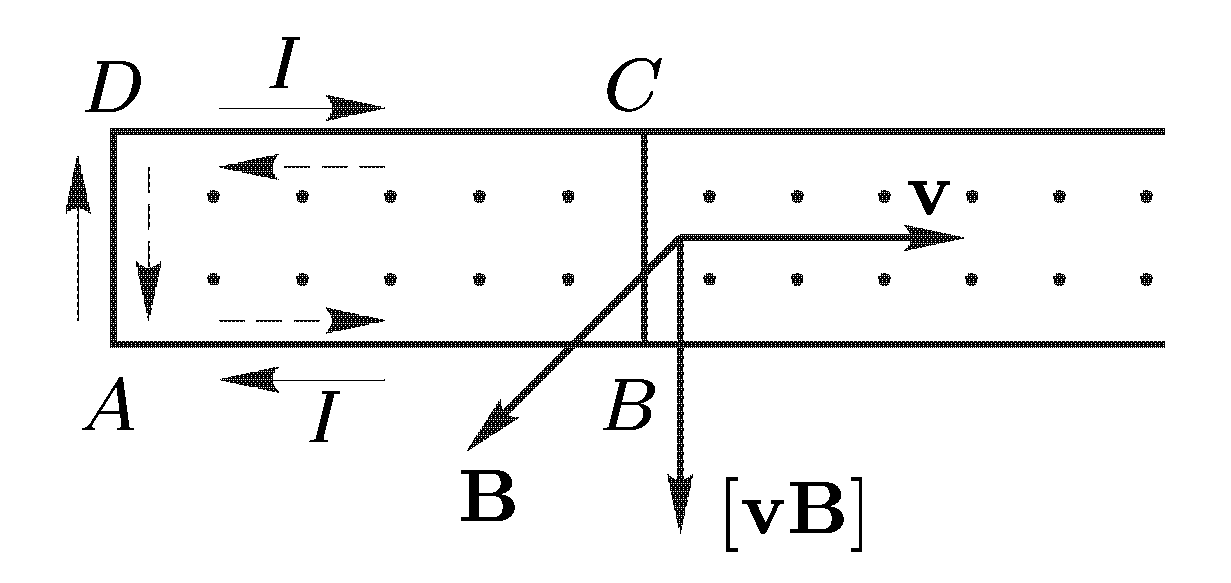
Рис.1.

При движении подвижного проводника так, как показано на рисунке направление тока и силы на положительные заряды будет вниз. Вычислим циркуляцию этой силы по замкнутому контуру (это и будет ЭДС):

(1)

где - магнитный поток через контур. То есть роль сторонней силы играет сила Лоренца. Формула (1) имеет место для произвольного контура и произвольного движения контура. А что будет, если контур неподвижен, а движется магнит, то есть изменяется магнитное поле? Тогда можно перейти в систему отсчета связанную с магнитом, в которой контур будет двигатьсяи в нем возникнет индукционный ток. Само явление индукционного тока от инерциальной системы не зависит. Следовательно, индукционный ток возникнет и в исходной системе, в которой контур неподвижен. К этому же выводу можно прийти из формулы преобразования полей. В системе отсчета магнита на заряды в контуре действует сила Лоренца, а в системе контура электрическая сила, причем силы должны быть равны:

(2)

Здесь есть скорости магнита в системе контура и скорость контура в системе магнита. Формула (2) показывает, что в системе контура возникает электрическое поле, циркуляция которого и будет равна ЭДС. Детальный анализ показывает, что и в этом случае ЭДС определяется формулой (1). Итак, мы приходим к выводу: при изменении магнитного потока через контур в внем возникает ЭДС, определяемая формулой

(3)

Это и есть закон электромагнитной индукции (закон электромагнитной индукции Фарадея). Знак минус в формуле перед производной означает, что возникающий в результате ЭДС индукционный ток направлен так, что его магнитное поле препятствует изменению магнитного потока.

К еще более фундаментальному выводу мы приходим, если внимательно проанализировать возникновение ЭДС путем перехода в движущуюся относительно магнита систему отсчета. Рассмотренные нами ранее формулы преобразования полей

(4)

(5)

Имеют общий характер. Именно они позволяют утверждать, что изменяющееся магнитное поле порождает электрическое поле, циркуляция которого не равна нулю. Такое поле называется вихревым. Переменное магнитное поле порождает вихревое электрическое поле в пространстве, безотносительно наличия контура с током. Если записать соотношене (3) для произвольного контура

(6)

Последнее рассуждение называется максвелловской трактовкой явления электромагнитной индукции.

Рассмотрим теперь вопрос об энергии токов, которая называется магнитной энергией. Ход рассуждений будет примерно такой же, как и при рассмотрении энергии электрических зарядов и энергии электрического поля. Рассмотрим сначала одиночный замкнуты виток. Пусть в начальный момент сила тока в нем равна нулю. Создадим и будем наращивать в нем ток. В результате появится переменное магнитное поле, переменный поток магнитного поля через виток и ЭДС, которая будет препятствовать наращиванию тока. Совершаемая внешними сиоами работа будет равна

(7)

где - магнитная энергия. Определим коэффициент индукцию контура (точнее коэффициент самоиндукции) с током соотношением

(8)

Тогда из (7) получаем

(9)

Формула (9) также может рассматриваться (наряду с формулой (8)) как определение коэффициента самоидукции. Теперь обобщим результат на случай произвольного число контуров (аналог энергии системы зарядов). Для бесконечно малой работы против сил самоиндукции

Для простоты будем наращивать ток синхронно . Тогда для магнитной энергии получаем выражение

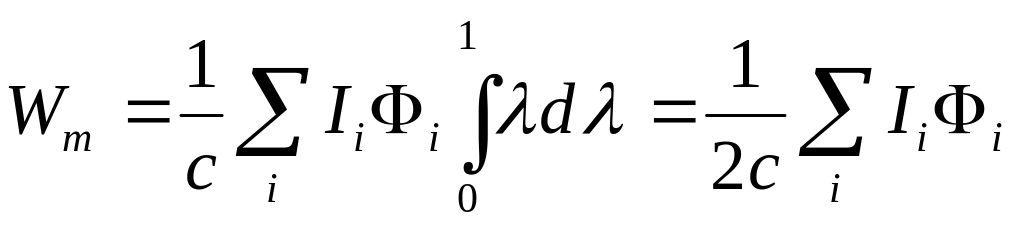(10)

Аналогично (8) определим коэффициенты взаимной индукции соотношениями

(11)

что для магнитной энергии дает формулу

(12)

Мы представили магнитную энергию токов как объектов, взаимодействующих силами Ампера. Это соответствует взаимодействию на расстоянии. Для интерпретации этой энергии как энергии магнитного поля получаем выражения (в скобках выражение для магнетиков, смотри приложение к лекции):

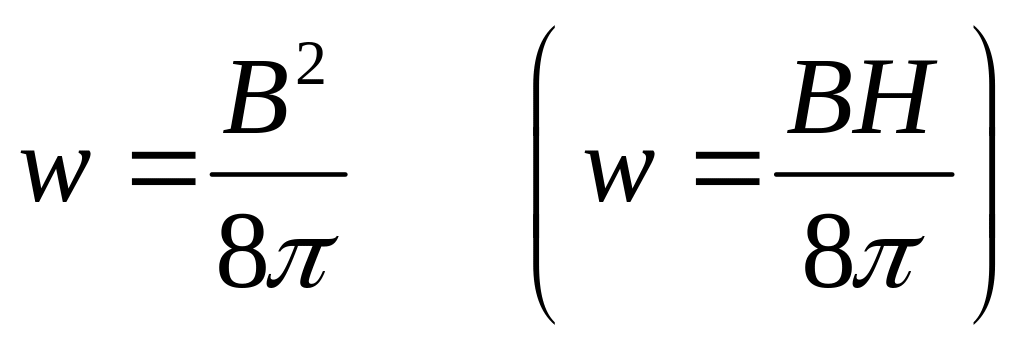(13)

Итак, мы с вами в разных разделах уже встречались со следующими уравнениями

(14)

Первое уравнение –выражает факт отсутствия магнитных зарядов в природе, второе –закон электромагнитной индукции, третье –теорему Гаусса в дифференциальной форме, четвертое теорему о циркуляции для напряженности магнитного поля в дифференциальной форме. И плотность заряда и плотность тока учитывают только свободные заряды. Мы также знаем, что должен выполняться фундаментальный закон – закон сохранения заряда

(15)

Но, взяв дивергенцию от четвертого уравнеия (14), мы получим

что возможно, только при . Следовательно, уравнения (14) непригодны для описания задач с переменной по времени плотностью заряда. Нетрудно увидеть как подправить уравнения (14), чтобы при взятии дивергенции от (14), получалось правильное уравнение непрерывности:

В результате мы приходим к системе уравнений Максвелла в дифференциальной форме

(16)

Добавление члена в правую часть четвертого уравнения(14) эквивалентно добавлению к плотности тока члена , который называется плотностью тока смещения. Необходимость введения тока смещения обосновал Максвелл, он же выписал систему уравнений (16), которая описывает любое электродинамическое явление. К необходимости введения такого члена можно подойти и путем анализа некоторых экспериментальных ситуаций. Разобрать две из них: заряженный шар в проводящей среде, разрядка плоского конденсатора.

Уравнения Максвелла могут быть записаны и в дифференциальной форме. Для этого их нужно проинтегрировать по произвольному объему или поверхности и воспользоваться формулами Остроградского-Гаусса и Стокса. В результате стандартных процедур получаем уравнения

(17)

Формулы (16,17) дают уравнения Максвелла в веществе. Плотности заряда и плотности тока относятся к свободным зарядам и свободным токам. К ним надо еще присоединить материальные уравнения дающие связь напряженностей с индукциями, которые в простейшем случае имеют вид

(18)

Для вакуума уравнения получаются совсем просто :

(19)

(20)В

уравнениях (19,20) плотности заряда и плотности тока включают все заряды и все токи.

Приложение1. Вывод выражения для плотности магнитной энергии.

Сила взаимодействия двух витков с током равна (лекция 7).

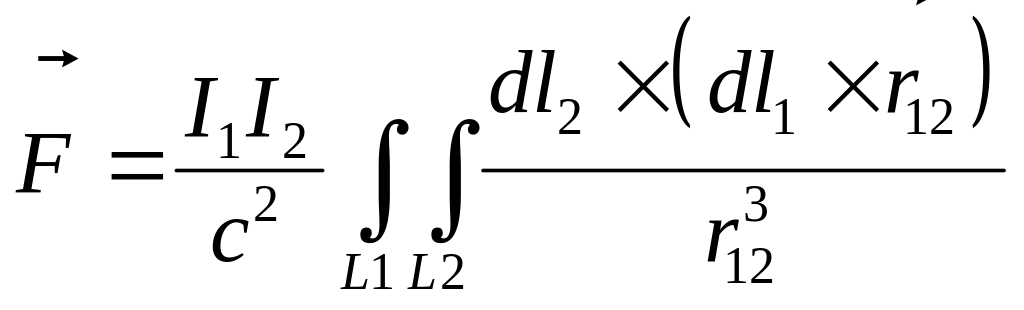(П1)

Для простоты обозначаем и записываем выражение для потенциальной энергии как

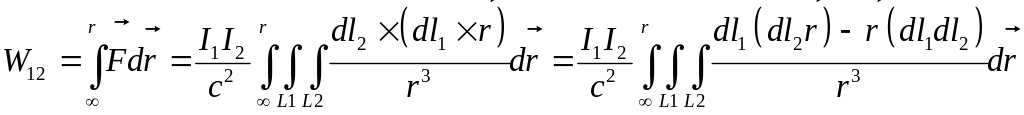(П2)

При интегрировании по первому контуру интеграл от первого слагаемого дает нуль (контур замкнут), а интеграл по второму контуру равен

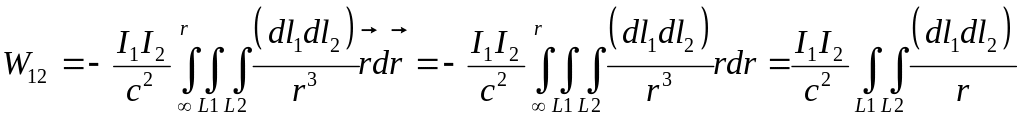(П3)

Переходим от локализованных к плотностям токов, к интегрированию по объемам (что означает суммирование по крнтурам) и вводим векторный потенциал

(П4)

При этом мы учли множитель так как при суммировании каждая пара учитывается дважды. Используем уравнения (теорему о циркуляции) и формулы векторного анализа

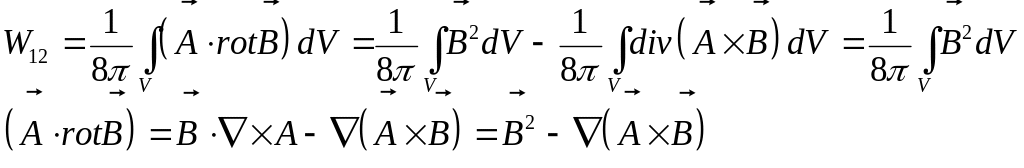(П5)

Где интеграл от дивергенции как обычно равен нулю. Откуда видно, что плотность магнитной энергийй (энергии магнитного поля) равна

(П6)

Для магнетиков аналогично получаем выражение (в скобках для сравнения энергия электрического поля)

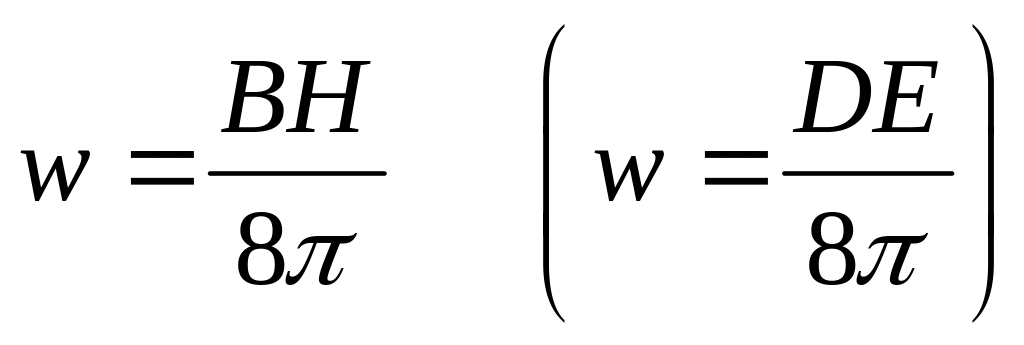(П7)

Лекция 11.

Уравнения для скалярного и векторного потенциалов, калибровочная инвариантность. Волновые уравнения, плоские однородные электромагнитные волны. Поток энергии, вектор Пойнтинга, закон сохранения энергии. Левые среды.

Давайте теперь исходить из уравнений Максвелла и анализировать электромагнитные явления на их основе. Еще раз выпишем уравнения Максвелла

(1)

Введем векторный потенциал, который мы на самом деле уже вводили, следующим соотношением

(2)

Тогда первое уравнение в (1) выполнится автоматически (для любого ), а второе даст

(3)

Откуда следует, что выражение под знаком ротора можно считать градиентом некоторой функции

(4)

Видно, что введенная скалярная функция является скалярным потенциалом, который мы уже встречали. Далее, третье и четвертое уравнения в (1) дадут (вместе с материальными уравнениями):

Лекция 12.

Закон сохранения энергии, вектор Умова-Пойнтинга. Давление и импульс электромагнитной волны. Волновая природа света. Поляризация света. Отражение и преломление волн на границе раздела, формулы Френеля. Полное внутреннее отражение. Интерференция и дифракция электромагнитных волн.

Лекция 13.

Переменные токи в цепях. Правила Кирхгофа для переменного тока. Метод векторных диаграм, метод комплексных амплитуд. Уравнение колебательного контура и его решение. Волны вдоль проводов, телеграфное уравнение.

Лекция 14.

Скин эффект. Движение частиц в электромагнитном поле. Эффект Холла, квантовый эффект холла. Электродинамика сверхпроводников.

Лекция 15. (математическое дополнение)

Дифференциальные операторы и интегральные теоремы векторного анализа, основные формулы векторного анализа. Декартова, цилиндрическая и сферическая системы координат. Понятие об обобщенных функциях. Метод разделения переменных. Ряды и интегралы Фурье.

Основные задачи к курсу электричество и магнетизм.

57. Дайте определение вектора намагниченности.

Вектор намагниченности связан с плотностью молекулярных токов соотношением

, а с поверхностной плотностью токов формулой .

58. Что называется напряженностью магнитного поля. В чем его смысл?

Напряженностью магнитного поля называется вспомогательный вектор равный

Для напряженности магнитного поля имеет место теорема о циркуляции вида:

В правую часть входят только токи свободных носителей (и не входят молекулярные токи).

Как правило, молекулярные токи неизвестны. Поэтому находить проще не индукцию, а напряженность магнитного поля. Напряженность измеряется в тех же единицах, что и индукция, но при этом по историческим причинам гаусс называют эрстедом. По смыслу, напряженность магнитного поля аналогична индукции электрического поля (а названия этого не отражают).

59. Какой вид имеют граничные условия на границе магнетиков?

Здесь единичный вектор нормали (из второй среды в первую), - плотность поверхностного тока.

60. Сформулируйте закон электромагнитной индукции (закон Фарадея).

61. Чему равна энергия витка с током?

где - индуктивность витка, - ток в витке, магнитный поток через поверхность витка, создаваемый током в витке.

62. Чему равна объемная плотность энергии магнитного поля?

63. Что такое ток смещения?

Плотностью тока смещения, током смещения называются величины:

Их необходимо включить в уравнения для циркуляции магнитного поля, чтобы сохранить уравнение закона сохранения электрического заряда. Ток смещения был введен Максвеллом.

Его смысл: переменное электрическое поле порождает магнитное поля. Аналогичную роль играет закон электромагнитной индукции Фарадея (переменное магнитное поле порождает электрическое)

64. Выпишите уравнения Максвелла в интегральной форме.

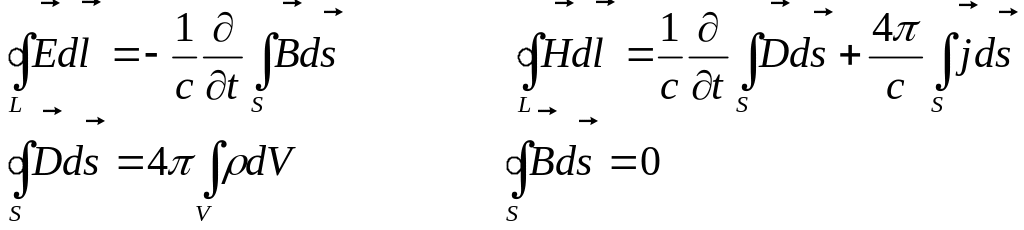
65. Выпишите уравнения Максвелла а дифференциальной форме.

66. Чему равны комплексные импедансы активного сопротивления, емкости, индуктивности?

Для переменного гармонического тока вводится понятие комплексного импеданса, который описывает связь между напряжением и током:

Для активного сопротивления, емкости: и индуктивности имеем:

67. Сформулируете законы Киркгофа при гармонической зависимости токов и напряжений от времени.

Первый закон Киркгофа: Алгебраическая сумма (входящие с плюсом, выходящие с минусом) токов для любого узла равна нулю:

Второй закон Киркгофа: Для любого замкнутого контура алгебраическая сумма падений напряжений равна алгебраической сумме ЭДС

В сумме слева берется знак плюс, если направление обхода контура совпадает с направлением тока, и знак минус в противном случае. В сумме справа берется знак плюс, если направление обхода контура внутри источника ЭДС идет от минуса к плюсу, и знак минус в противном случае.

Указанный выбор знаков можно производить в любой фиксированный момент времени, например, при . ЭДС также имеет гармоническую зависимость от времени .

68. Выпишите волновые уравнения.

69. Что такое вектор Умова-Пойнтинга?

Вектор Умова-Пойнтинга дает плотность потока энергии (энергия проходящая через единичную площадку, перпендикулярную направлению распространения волны, в единицу времени:

70. Какая волна называется плоской, однородной, гармонической волной?

Решение волнового уравнения вида

Называется плоской, однородной, гармонической волной. - волновой вектор, описывающий направление распространения волны, - круговая частота, , амплитуды волн, вектора образуют правую тройку взаимно перпендикулярных векторов.

71. Как связан волновой вектор и частота? Что такое фазовая скорость волны?

72. Какие вещества называются парамагнетиками, диамагнетиками, ферромагнетиками?

Парамагнетиками называются вещества, у которых (чуть больше единицы).

Диамагнетиками называются вещества, у которых (чуть меньше единицы).

Ферромагнетиками называются вещества, у которых .

Кроме того, у парамагнетиков и диамагнетиков намагниченность в отсутствии внешнего магнитного поля равна нулю, а у ферромагнетиков может существовать спонтанная, ненулевая намагниченность даже в отсутствие внешнего магнитного поля.