Порядок выполнения работы

Эксперимент 1. Изучение основных понятий, связанных с отражением объектов детерминистского физического мира в наших мыслительных образах в виде материальной точки (частицы), пространства и движения.

Изучение того, что такое окружающий нас физический мир удобно начинать с общего научного подхода, который получил название механического детерминизма.

Детерминизм - общенаучное понятие о причинности, закономерности, генетической связи, взаимодействии и обусловленности всех явлений и процессов, происходящих в мире. Термин детерминизм происходит от лат. determino (определяю).

Механический детерминизм это некоторая иллюзорная точка зрения на мир, на то, что происходит в этой жизни. Согласно такому взгляду на мир объективная реальность представляется только во всем существенном, как четко определенный набор закономерностей, как действие детерминистских законов природы. Детерминизм утверждает, что все происходящее вокруг нас реализуется в соответствии с жестко заданной цепью причин и следствий. При развитии любого процесса всегда имеется одна возможность. Каждая траектория единственным образом определяется начальными условиями. Здесь возможность и действительность в точности совпадают.

Если говорить несколько иначе, то в случае механического детерминизма мы рассматриваем лишь определенную сторону реальности, которая связана с «существенным», важным для нас. Случайности, имеющие место, которые часто нам не слишком мешают, во всяком случае, в практической деятельности, мы относим к «несущественному». При таком подходе для некоторого идеализированного наблюдателя нет никакой случайности. Не вписывающиеся в детерминированную картину сомнительные моменты и возникающие все-таки в реальности разные случайности, принято относить к неполноте наших представлений о явлениях.

Концепция механического детерминизма была и остается фундаментом классический механики и физики. Суть ее в том, что силы (то есть некоторые внешние причины и факторы), действующие на материальную систему и ее начальное состояние, жестко и однозначно определяют историю всех дальнейших событий и состояний. Всё определено в этом мире, всякое действие вызывает однозначное следствие и ничто не в состоянии этого изменить.

При таком подходе все величины связаны математическими зависимостями в форме линейных, дифференциальных и интегральных уравнений. Вам известно, что классическая физика, особенно возникшая раньше других разделов физики механика, многие годы была ориентирована на изображение закономерностей объективной реальности именно такими средствами.

Для понимания основ физической детерминистской картины мира при скоростях тел, малых по сравнению со скоростью света, оказывается вполне достаточным понимание такой сущности, как пространство, а также знаний о классической (ньютоновой) механике, которая изучает движение системы частиц в пространстве.

Пространство в детерминистской картине мира обладает свойством однородности и изотропии, имеет три измерения. В масштабах, привычных для человека, пространство имеет три пространственных измерения. Это может быть «длина», «ширина» и «высота» комнаты, в которой Вы сейчас находитесь.

Понимание того, что представляет собой пространство, является важным для экономиста, поскольку работа с имеющими координатную привязку объектами в настоящее время является сущностью бурно развивающегося рынка.

В ряду нужной информации большая ее часть состоит из пространственных данных, то есть из различных сведений о распределенных в пространстве или по территории объектах, явлениях и процессах. В простейшем случае понимание пространства позволяет получить ответы на такие вопросы: где в пространстве располагаются Ваши клиенты, куда им удобнее пойти за покупками, как это все им доставить с наименьшими затратами, где выгоднее открыть новый магазин или сервисный центр, где находятся Ваши партнеры и конкуренты? Пространственные представления используются и в других областях бизнеса: для оптимального по разным критериям выбора местоположения новых филиалов фирмы или банка, торговых точек, складов, производственных мощностей; для выбора кратчайших или наиболее безопасных маршрутов перевозок и путей распределения продукции; для определения привязанного к территории спроса на продукцию; при создании и географической привязке данных о земле- и домовладении. Использование пространственных представлений необходимо при массовых перевозках грузов и людей, при создании сетей оптимально размещенных торговых точек, при анализе существующих и потенциальных рынков и районов сбыта продукции, в нефтяных, газовых и электрических компаниях, а также в коммерческих фирмах, занимающихся операциями с недвижимостью, в работе авиакомпаний и телекоммуникационных корпораций.

При детерминированном подходе удобно пользоваться абстрактным (идеализированным) понятием материальной точки – то есть телом, не имеющем размеров, формы и внутренней структуры. Материальная точка – это бесструктурный объект, её движение – элементарно, её эволюция – это изменение бесструктурной сущности в самом элементарном исполнении, заключающемся лишь в изменении положения по отношению к системе координат. Материальная точка – это некое макроскопическое тело, размерами которого можно пренебречь при описании его движения. Часто такое тело называют частицей.

Механика материальной точки является основой всей механики. Раздел механики, в котором изучаются способы описания движения независимо от причин, обусловливающих его, или по-другому, геометрические свойства движения тела без учета его массы и действующих сил, получил название кинематики.

Со времени зарождения научного знания для понимания пространства в естествознании использовались различные формы представления точки в пространстве. Для характеристики местоположения частицы в пространстве и описания ее движения часто используют три способа:

1. Координатный.

2. Векторный.

3. Траекторный (естественный).

Наиболее широко для описания положения (местоположения) и движения частицы используют координатный способ, который использует понятия «система отсчета» и «координаты точки».

При таком способе с частицей жестко связывают определенную систему координат, как правило, ортогональную, то есть систему с взаимно перпендикулярным направлением осей. Наиболее часто применяют правую прямоугольную декартову систему координат) (в дальнейшем просто – декартову), а также цилиндрическую (как частный случай –полярную) или сферическую систему координат. Выбор системы координат определяется постановкой задачи и стремлением упростить ее математическое решение. При использовании координатного способа движение частицы представляется посредством математических моделей прямых и кривых линий.

На практике широкое применение находит наиболее простая прямоугольная система координат на плоскости (2D). Она представляет собой две взаимно перпендикулярные оси, имеющие общее начало. Нижняя ось называется осью абсцисс, а вертикальная – осью ординат. Точка пересечения называется началом координат.

Если точка М произвольная точка (положение частицы) на плоскости, и опустить перпендикуляры на оси, то полученные координаты проекций точки М называются абсциссой и ординатой. Соответственно, при выбранной системе координат каждой точке М плоскости соответствует единственная пара чисел (x1;y1) – ее прямоугольные координаты. И, обратно, каждой паре чисел (x1;y1) соответствует и притом одна точка М(x1;y1) на плоскости.

Таким образом, введение прямоугольной системы координат на плоскости позволяет установить взаимно однозначное соответствие между множеством всех точек плоскости (положений частиц) и множеством пар чисел, что дает возможность применять алгебраические методы.

Рис.01. Вектор и его проекции на координатные оси

Введите в командное окно MATLAB програму 1.

Имейте при этом в виду, что с помощью мышки наведением перекрестья Вы должны вывести текст на график: название точки и координаты проекций точки М на ось абсцисс и ординат.

Сделайте вывод о том, чем при координатном способе характеризуют местоположение частицы (точки) М(x1;y1) в двумерном пространстве (на плоскости).

Програма 1.

clear;

format short

x1=4

y1=5

plot(x1,y1,'b.','MarkerSize',24)

xlabel('Koordinata X');

ylabel('Koordinata Y');

grid on

gtext('M(x1,y1)=M(4,5)')

gtext('x1=4')

gtext('y1=5')

Если частица под действием какой-то причины поменяла свое положение, то говорят, что частица переместилась на плоскости из одной точки «а» в другую «b» или осуществила движение по пути ab.

Рис.02. Перемещение частицы из точки «а» в другую точку «b» по кратчайшему пути ab и по криволинейной траектории

Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина. Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина. Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.

В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения . При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.

Обратите внимание на то, что модуль вектора перемещения, отображающий пройденное расстояние, представляет собой характеристику пространства. В частности, расстояние представляет собой меру того, сколько пространства расположено между двумя точками. Промежуток времени Δt, представляет собой характеристику времени, а именно промежутка времени между событиями. Связывает понятия пространства и времени скорость.

В простейшем случае движение частицы может осуществляться по линии, параллельной одной из осей координат. В этом случае путь пройденный частицей s определяется величиной изменения координаты. Если движение осуществляется по прямой, наклонной к осям, то пройденный путь оценивают, пользуясь теоремой Пифагора. Для любых двух положений частицы А(x1;y1) и В(x2;y2) , заданных координатами, кратчайшее расстояние (путь) s между ними определяется формулой

Введите в командное окно MATLAB.

Имейте при этом в виду, что с помощью мышки наведением перекрестья Вы должны вывести текст на график названия точек А, В, С.

Сделайте вывод о том, чем при координатном способе характеризуют изменение местоположения частицы (точки) М(x1;y1) (перемещение тела) в двумерном пространстве (на плоскости).

Програма 2.

clear;

x=[4 4 7];

y=[5 9 5];

plot(x,y,'b.','MarkerSize',24)

xlabel('Koordinata X');

ylabel('Koordinata Y');

grid on

axis([3,8,4,10]);

gtext('A(x1,y1)')

gtext('B(x2,y2)')

gtext('C(x3,y3)')

sAB=sqrt((x(2)-x(1))^2+(y(2)-y(1))^2)

sAC=sqrt((x(3)-x(1))^2+(y(3)-y(1))^2)

sBC=sqrt((x(3)-x(2))^2+(y(3)-y(2))^2)

Помимо координатного способа описания местоположения также используют векторный способ описания движения частицы. При таком способе положение интересующей нас частицы А задают радиус-вектором , проведенным из некоторой неподвижной точки О, выбранной в качестве начала отсчета, в точку А. Радиус-вектор характеризуется длиной и углом поворота.

Вам также известно, что любой вектор может быть однозначно определен своими проекциями на оси, направление которой однозначно определено так называемым единичным вектором-ортом. Единичные вектора вдоль направлений координатных осей ОХ, OY, OZ обычно обозначают: . Эту тройку ортогональных ортов называют базисом координатной системы.

Радиус-вектор , проведенный из некоторой неподвижной точки О, выбранной в качестве начала отсчета, в точку А может быть представлен проекциями вектора на орты

.

Рис.02. Определение положения точки с помощью координат x = x (t), y = y (t) и z = z (t) и радиус-вектора . – радиус-вектор положения точки в начальный момент времени

Проекцией «а_U» вектора на ось u (например, на ось х или у) называется отрезок аb, отсекаемый на этой оси перпендикулярными к ней плоскостями, которые проведены через концы вектора . Размер проекции определяется числом, равным длине отрезка аb и знаком.

Проекция вектора величина алгебраическая, то есть ее знак определен углом между данным вектором и положительным направлением оси u. Если угол между вектором и ортом острый – проекция положительна, если тупой – отрицательна, а если угол прямой – проекция равна нулю.

Введите в командное окно MATLAB.

Имейте при этом в виду, что с помощью мышки наведением перекрестья Вы должны вывести текст на график названия точек О и А, а также проекции вектора на направление координатных осей ОХ и OY.

Програма 3.

clear; format short

TO=0+i*0;

TA=3+i*4;

vekAO=[TO TA];

compass(vekAO)

gtext('O(o,o)')

gtext('A(xa,ya)')

gtext('Proek(xa)')

gtext('Proek(ya)')

Proek_xa=real(TA)

Proek_ya=imag(TA)

В общем случае, при перемещении в пространстве частицы М меняются модуль и направление радиус – вектора . Геометрическое место точек пространства, где частица А побывала за время своего движения называется ее траекторией. При векторном способе описания траекторией будет кривая, описываемая концом радиус вектора во все моменты времени ее движения (годограф векторной функции).

Введите в командное окно MATLAB.

Имейте при этом в виду, что с помощью мышки наведением перекрестья Вы должны вывести текст на график названия точек А и В, начала и конца движения частицы.

Сделайте вывод о том, чем при векторном способе характеризуют изменение местоположения частицы (точки) М(x1;y1) (перемещение тела) в двумерном пространстве (на плоскости).

Програма 4.

clear; TO=[0+i*0 0+i*0 0+i*0 0+i*0 0+i*0] ;

TA=[-5+i*0.5 -4+i*1 -3+i*2 -2+i*5 -1+i*7];

godogrAB=[TO TA];

compass(godogrAB)

gtext('A(xa,ya)')

gtext('B(xb,yb)')

Мысленно представьте себе вид кривой, описываемой концом радиус – вектора и сделайте вывод о том, является ли годограф прямой линией.

Для описания положения и движения частицы используют также траекторный (естественный) способ. Этот способ применяют в том случае, когда заранее известна траектория частицы.

Траектория описывается (в заданной системе координат) уравнением кривой L . Этому уравнению удовлетворяют координаты х и у любой точки, лежащей на кривой L и не удовлетворяют координаты никакой другой точки не лежащей на этой кривой. Другими словами, траектория L частицы представляет собой множество всех точек плоскости, координаты которых удовлетворяют уравнению .

В полярных координатах траектория L может определяться уравнением вида ,

где - полярные координаты частицы.

Сделайте вывод о том, чем при траекторном способе характеризуют изменение местоположения частицы.

Введите в командное окно MATLAB.

Имейте при этом в виду, что с помощью мышки наведением перекрестья Вы должны вывести текст на график названия кривой.

Програма 5.

clear;

t=[0:0.01:0.5*pi];

x=0.8*sin(t);

y=0.8*cos(t).*cos(t);

plot(x,y,'k','linewidth',2)

xlabel('Koordinata X');

ylabel('Koordinata Y');

grid on

gtext('L(x,y)')

На практике для характеристики перемещений в пространстве, помимо кривых первого порядка – прямых линий, используют кривые второго порядка, уравнения которых в прямоугольной системе координат являются уравнениями второй степени. В частности, для описания пространственного перемещения частиц используется окружность и эллипс.

Каноническое (или простейшее) уравнение эллипса имеет вид

.

Эллипс является симметричной фигурой. Центр его симметрии находится в точке пересечения осей х и у.

Если х=a, то у=0. Точка А(а,0), в которой эллипс пересекает положительную горизонтальную ось системы координат XOY получил название большой вершины эллипса.

Если х=0, то у=a. Точка В(0,b), в которой эллипс пересекает положительную вертикальную ось системы координат XOY получил название малой вершины эллипса. Расстояния от начала координат до точек a и b называют соответственно большой и малой полуосями эллипса.

Меру вытянутости эллипса по осям характеризует эксцентриситет

.

Эксцентриситет геометрически истолковать можно следующим образом. Если эллипс близок к окружности и его a и b почти равны, то эксцентриситет . Если величина малой полуоси b весьма мала по сравнению с числом а, то эллипс сильно вытянут вдоль большой полуоси и его эксцентриситет .

Введите в командное окно MATLAB програму.

Изучите два случая

а) величина большой полуоси [Bol os A(a,0)] а=1.8 величина малой полуоси [Mal os B(o,b)] b =1.1;

б) величина большой полуоси а=1.4 величина малой полуоси b =1.4;

Имейте при этом в виду, что с помощью мышки наведением перекрестья на график Вы должны вывести текст, указывающий названия большой и малой полуосей эллипса.

Програма 6.

clear;

Z=inputdlg({'Bol os A(a,0)','Mal os B(o,b)'});

disp( 'Величина большой полуоси эллипса')

a=str2num(Z{1})

disp( 'Величина малой полуоси эллипса')

b=str2num(Z{2})

h1=warndlg('Проверьте правильность введенных данных'...

,'Указание2');

set(h1,'WindowStyle','modal')

waitfor(h1)

t=[0:0.01:2*pi];

x=a*sin(t);

y=b*cos(t);

plot(x,y,'k','linewidth',2)

xlabel('Koordinata X');

ylabel('Koordinata Y');

axis([-3,3,-2,2]);

grid on

gtext('Bol os A(a,o)')

gtext('Mal os B(o,b)')

disp( 'Величина эксцентриситета эллипса')

exent= sqrt(1-((b/a)*(b/a)))

При картографировании сложную фигуру геоида Земли заменяют математически более простой - эллипсоидом вращения – геометрическим телом, которое образуется при вращении эллипса вокруг малой его полуоси.

В 1940 году Ф. Н. Красовский с учениками выполнил расчет эллипсоида, который был утвержден в СССР для геодезических и картографических работ. Со временем повышалась точность определения полуосей. В настоящее время используют эллипсоид WGS -84 (Word Geodetic System,1884), получивший мировое распространение благодаря американской глобальной системе спутникового позиционирования, и российский ПЗ-90 (Параметры Земли, 1990). Параметры основных земных эллипсоидов приведены в таблице 1.

Таблица 1

Параметры	WGS-84	ПЗ-90	Красовского
Большая экваториальная полуось, а, м	6378137	6378136	6378245
Малая полярная полуось, b, м	6356752.314	6356751.362	6356863.019

Введите в командное окно MATLAB програму.

Рассчитайте параметры трех эллипсоидов

Програма 7.

clear;

Z=inputdlg({'Bol ekv os A(a,0)','Mal polar os B(o,b)'});

disp( 'Величина экваториальной полуоси эллипса')

a=str2num(Z{1})

disp( 'Величина полярной полуоси эллипса')

b=str2num(Z{2})

h1=warndlg('Проверьте правильность введенных данных'...

,'Указание2');

set(h1,'WindowStyle','modal')

waitfor(h1)

t=[0:0.01:2*pi];

x=a*sin(t);

y=b*cos(t);

plot(x,y,'k','linewidth',2)

xlabel('Koordinata X');

ylabel('Koordinata Y');

axis([-8000000,8000000,-8000000,8000000]);

grid on

gtext('Bol os A(a,o)')

gtext('Mal os B(o,b)')

disp( 'Величина эксцентриситета эллипса')

exent= sqrt(1-((b/a)*(b/a)))

Эксперимент 2. Изучение основных характеристик движения материальной точки (частицы) в пространстве

Введение понятий координат и перемещений материальной точки позволяет исследовать ее пространственно - временные перемещения и ввести скорость и ускорение. Для описания движения частицы в кинематике используются понятия закона движения частицы и такие ее характеристики, как перемещение, скорость, ускорение материальной точки.

Закон движения частицы – это зависимость координат от времени. Он задает положение и перемещение вдоль траектории частицы, ее скорость и ускорение в каждый момент времени.

Поскольку описание движения частицы зависит от выбранной системы координат, то в кинематике первым делом нужно выбрать систему координат и задать начало отсчета времени. Без выбора системы отсчета описать движение невозможно.

Рассмотрим, в качестве примера, один из видов основных движения - поступательное движение.

Чтобы стало понятно, что такое поступательное движение, сделаем небольшое отступление.

В реальности вы сталкиваетесь с абсолютно твердыми телами, как со следующей по сложности моделью после частицы. Абсолютно твердое тело – совокупность материальных точек, в которой расстояние между любыми двумя точками не меняется в процессе движения. Для абсолютно твердого тела поступательное движение это такой вид движения, когда прямая, соединяющая две любые точки тела, перемещается, оставаясь параллельной своему начальному положению.

При поступательном движении все точки твердого тела совершают равные перемещения за один и тот же промежуток времени. Поэтому скорости и ускорения всех точек тела в данный момент времени одинаковы. Этот факт позволяет свести изучение поступательного движения твердого тела к изучению движения отдельной точки тела, то есть к задаче о кинематике частицы. Таким образом, поступательное движение твердого тела может быть полностью описано, если известны зависимость от времени радиус вектора любой точки этого тела. При этом следует иметь в виду, что ряд движений имеет специальное название. Так движение с постоянным вектором ускорения называется равнопеременным, а движение с постоянным вектором скорости – равномерным.

Вам известно, что описание движения в различных системах координат эквивалентны между собой в том смысле, что при известном расположении двух систем координат относительно друг друга, по величинам, найденным в первой системе, можно определить соответствующие величины во второй. Тем не менее, из соображений целесообразности разумно выбирать такую систему координат, в которой уравнения, описывающие движение, получаются проще.

Вы в школе уже изучали механическое движение частицы на основе координатного метода, тесно связанного с выбранной прямоугольной системой отсчета OXY. В прямоугольной системе координат вектор , который определяет положение интересующей нас частицы относительно начала координат О в момент времени t, может быть представлен проекциями радиус – вектора на оси координат: .

Вам хорошо известно, что при прямолинейном поступательном движении система уравнений получается проще, если берется ось координат, направленная вдоль движения. При этом лишь одна координата при движении частицы будет возрастать или убывать в зависимости от того, куда направлен вектор движения.

Введите в командное окно MATLAB програму.

Изучите, как материальная частица поступательно перемещается вдоль оси ОХ с постоянной скоростью.

Програма 8.

clear;

t=[0:0.0001:1];

x=1.*t;

y=cos(t).*cos(t)+sin(t).*sin(t);

plot(x,y,'k--')

xlabel('Koordinata X');

ylabel('Koordinata Y');

hold on

comet(x,y)

В этом случае мы имеем дело с прямолинейным равномерным поступательным движением вдоль одной координаты, когда движение частицы происходит с постоянной скоростью (материальная точка за равные промежутки времени проходит одинаковые расстояния)

Введите в командное окно MATLAB програму.

Изучите, как материальная частица поступательно перемещается вдоль оси ОХ с уменьшающейся скоростью.

Сравнивая виды поступательного движения вдоль прямой линии, сделайте вывод о том, чем они различаются.

Програма 9.

clear;

t=[0:0.001:18];

x=6.*t-(0.25).*t.*t;

y=cos(t).*cos(t)+sin(t).*sin(t);

plot(x,y,'k--')

xlabel('Koordinata X');

ylabel('Koordinata Y');

hold on

comet(x,y)

В этом случае при движении частицы изменение скорости происходит не пропорционально времени и, соответственно, мы имеем дело с прямолинейным неравномерно ускоренным (точнее неравномерно замедленным) поступательным движением вдоль одной координаты. В этом случае скорость и ускорение являются функциями времени: .

Всякое криволинейное движение является сложным движением, то есть при криволинейном движении частица одновременно участвует в нескольких движениях.

При криволинейном движении используют принцип независимости движений: если частица участвует одновременно в нескольких движениях, то каждое из этих движений происходит независимо от других. При криволинейном движении приходится брать прямоугольную систему координат с двумя осями и представлять движение в виде двух движений, происходящих вдоль осей координат ОХ и OY. Причем и в этом случае уравнения получаются проще, когда направления осей выбраны так, что проекции движущейся частички в течение всего времени движения равны нулю.

Введите в командное окно MATLAB програму.

Изучите, как материальная частица поступательно перемещается вдоль осей координат ОХ и OY, совершая криволинейное движение.

Програма 10.

clear;

t=[0:0.001:10];

x=sin(t)./(t+1);

y=cos(t)./(t+1);

plot(x,y,'k--')

xlabel('Koordinata X');

ylabel('Koordinata Y');

hold on

comet(x,y)

Координатное задание закона движения частицы, ее траектории движения не демонстрирует в явном виде зависимость пройденного частицей пути, скорости и ускорения от времени движения и от положения частицы. В этой связи для установления законов движения удобно пользоваться графиками, которые наглядно отражают соотношение между скоростью, перемещением, ускорением и временем. Такие графики позволяют определить величины скорости и ускорения в любой момент времени и перемещение частицы к этому моменту.

Следует иметь в виду, что скорость и ускорение являются векторными величинами. Они характеризуются величиной и направлением. Если движение частицы осуществляется в направлении, которое совпадает с какой-то одной осью координат, то проекция вектора на эту ось равна модулю вектора. Соответственно в этом случае вместо векторной величины можно оперировать скалярной величиной проекции на координатную ось. После введения проекций, механическое движение частицы можно анализировать на основе координатного способа.

Рассмотрим равномерное прямолинейное движение.

Будем при этом полагать, что частица перемещается вдоль оси ОХ. Поскольку нас интересует равномерное поступательное движение, то будем считать, что движение вдоль координаты происходит с постоянной скоростью и за равные промежутки времени частица проходит одинаковые расстояния. При этом проекция вектора перемещения на координату Х зависит от времени по закону

.

Величина пройденного пути (перемещения вдоль координаты), как следует из () будет равна площади прямоугольника, построенного на графике скорости с основанием равным величине затраченного на перемещение времени.

Закон равномерного поступательного движения, то есть зависимость координаты от времени , определяет не только положение частицы, но и позволяет найти ее скорость и ускорение в каждый момент времени. Используя координатный способ можно записать проекции, например, на ось Ох, векторов скорости и ускорения:

Проекции векторов скорости и ускорения на ось Ох равны соответственно первой и второй производным координат по времени.

Введите в командное окно MATLAB програму.

Проанализируйте графики, характеризующие как изменяется положение, скорость и ускорение частицы при равномерно поступательном движении вдоль оси координат ОХ, для случаев постоянной скорости, представленным в табл. 2. Определите путь, пройденный частицей за 60 секунд.

Таблица 2.

N п/п	Объект, который мы представляем частицей	Скорость материального объекта, м/с
1	Снаряд в полете	1000;
2	Самолет	900;
3	Звук в воздухе	3.3*1e2;
4	Автомобиль	20
5	Ветер силой 7 баллов	15
6	Высокоскоростной японский лифт	10
7	Пешеход	1.4
8	Тихоходный лифт	0.7

Програма 11.

clear;

disp( 'Объект, который мы представляем частицей:')

disp( 'автомобиль')

to=0;

t1=62;

Vo=20;%Введите значение скорости

n=1200;

t3=linspace(to,t1,n);

Xt=Vo.*t3;

disp( 'Путь, пройденный объектом в метрах')

disp( 'за одну минуту')

S60=Vo*60

Xtu=Xt(1:end-2);

delt=(t1-to)/(n);

Vx=(1/delt).*diff(Xt);

Vxu=Vx(1:end-1);

Xtu=Xt(1:end-2);

t=t3(1:end-2);

ax=(1/delt).*diff(Vx);

subplot(311);plot(t,Xtu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('X(t), m');

subplot(312);plot(t,Vxu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('V(t), m/c');

subplot(313);plot(t,ax,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('a(t), m/c^2');

Обратите внимание, что, решая задачу определения скорости и ускорения численно на компьютере, мы получаем не совсем точное решение, а лишь некоторое приближение к тому, что мы можем определить аналитически, по формулам. Если аналитически вычислять скорость, как первую производную координаты по времени, то она должна быть равна величине постоянной скорости . У нас получается приближенная к этому величина. Ускорение, как производная от постоянной величины , аналитически должна быть, по определению, равна нулю. Но мы наглядно видим при вычислении ускорения (дифференцирование координаты по времени производится дважды) вычислительные погрешности не равны нулю. Появление вычислительных погрешностей при определении скорости и ускорения связано с ограниченными техническими возможностями представления чисел в компьютере. Из-за ограничения разрядности представления чисел производные вычисляются не точно.

Однако получаемые в нашем случае результаты можно признать приемлемыми для практики, поскольку получаемые данные имеют относительно небольшую погрешность (колебания данных ускорения происходят вблизи нуля в девятом знаке после запятой).

Рассмотрим теперь поступательное движение, но когда скорость движения, а, соответственно и ускорение, меняются во времени по какому-то закону.

Введите в командное окно MATLAB програму.

Проанализируйте графики, характеризующие, как изменяется координата Х, скорость и ускорение частицы при поступательном движении вдоль оси координат ОХ, для случаев, представленных в табл. 3. Определите путь, пройденный частицей за 20 секунд.

Таблица 3.

N п/п	Вид поступательного движения	Начальная скорость, м/с	Постоянное ускорение, м/с2
1	Равномерно ускоренное	0	2
2	Равномерно ускоренное	60	2
3	Равномерно замедленное	60	-2
4	Равномерное	60	0

Програма 12.

clear;

Z=inputdlg({'Nach Ckopost, m/c','Uskorenie, m/c^2'});

disp( 'Начальная скорость в момент t=0')

Vo=str2num(Z{1})

disp( 'Постоянное ускорение')

ao=str2num(Z{2})

h1=warndlg('Проверьте правильность введенных данных'...

,'Указание2');

set(h1,'WindowStyle','modal')

waitfor(h1)

to=0;

t1=20;

n=1200;

t3=linspace(to,t1,n);

Vt=Vo+ao.*t3;

Vxu=Vt(1:end-1);

delt=(t1-to)/(n);

ax=(1/delt).*diff(Vt);

axu=ax;

t=t3(1:end-1);

Xt(1)=0;

for i=1:length(t3)-1

x1=t3(1:i+1);

y1=Vt(1:i+1);

Xt(i+1)=trapz(x1,y1);

end

Xtu=Xt(1:end-1);

subplot(311);plot(t,Xtu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('X(t), m');

subplot(312);plot(t,Vxu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('V(t), m/c');

subplot(313);plot(t,ax,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('a(t), m/c^2');

Поступательное равномерно ускоренное движение характеризуется тем, что оно имеет постоянное ускорение и скорость частицы растет прямо пропорционально времени. Типичные значения ускорений представлены в табл. 4.

Таблица 4.

№ п/п	Объект, который мы представляем частицей	Ускорение материального объекта, м/с2
1	Электрон в электронно-лучевой трубке телевизора	1015
2	Снаряд в стволе орудия	5х103
3	Летчик самолета перехватчика	50
3	Автомобиль	6
4	Пассажирский поезд	0,2

Ускорение на графике скорости характеризуется тангенсом угла наклона между касательной к графику скорости и осью времени. Если тело начинает двигаться равноускоренно из состояния покоя, то такое движение называют без начальной скорости. Очевидно, что поскольку движение начинается из состояния покоя, то скорость, достигнутая к моменту времени , будет равна . Если в момент тело обладало начальной скоростью то такое поступательное равномерно ускоренное движение называется с начальной скоростью.

График зависимости координаты х частицы от времени представляет собой кривую второго порядка. Пройденный частицей путь соответствует площади трапеции, построенной на графике скорости. Поскольку площадь трапеции можно представить как сумму прямоугольника и треугольника, то очевидно, что при движении из состояния покоя, перемещение равно площади треугольника на графике скорости.

При равнозамедленном движении (при замедлении имеет место отрицательное ускорение) скорость частицы уменьшается и она может остановиться или начать двигаться с отрицательной скоростью. Напомним. Что проекции ускорений и скоростей считаются положительными, если направление соответствующей составляющей совпадает с положительным направлением оси; в противном случае они записываются со знаком минус.

Если изменение скорости происходит не пропорционально времени, то есть ускорение не постоянно, то такое поступательное движение называется неравнопеременным. В этом случае скорость и ускорение являются функциями времени: ; . В каждый конкретный момент времени мы имеем дело с мгновенной скоростью и ускорением.

Введите в командное окно MATLAB програму.

Проанализируйте графики, характеризующие, как изменяется координата Х, мгновенные скорость и ускорение частицы при поступательном неравнопеременном движении вдоль оси координат ОХ. Чтобы придать полученным расчетам смысл, считайте, что по прямой движется автомобиль (частица), который изменяет скорость из-за того, что встречаются светофоры или впереди движется другой автомобиль.

Сделайте вывод о том, чем характеризуют движение частицы при поступательном неравнопеременном движении вдоль оси координат ОХ.

Програма 13.

clear;

to=0;

t1=20;

n=1200;

Vo=5;

ao=2;

t3=linspace(to,t1,n);

Vt=ao.*t3+4*Vo.*sin(t3/2);

Vxu=Vt(1:end-1);

delt=(t1-to)/(n);

ax=(1/delt).*diff(Vt);

axu=ax;

t=t3(1:end-1);

Xt(1)=0;

for i=1:length(t3)-1

x1=t3(1:i+1);

y1=Vt(1:i+1);

Xt(i+1)=trapz(x1,y1);

end

Xtu=Xt(1:end-1);

subplot(311);plot(t,Xtu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('X(t), m');

subplot(312);plot(t,Vxu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('V(t), m/c');

subplot(313);plot(t,ax,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('a(t), m/c^2');

figure

hist(Vt)

Vcp=mean(Vt)

По графику изменения координаты частицы можно определить расстояние пройденное частицей за данный промежуток времени. Чем круче наклон графика перемещения , тем больше в данный момент времени мгновенная скорость . Если известна зависимость перемещения частицы от времени , то мгновенная скорость определяется первой производной функции по времени

.

Если известна зависимость скорости от времени , то путь, пройденный частицей равен площади криволинейной трапеции, построенной на графике скорости, определяется интегралом

.

Для характеристики скорости часто используют понятие средней скорости. По определению средняя скорость есть

.

Надо иметь в виду следующее. Определение средней скорости как среднего арифметического начальной и конечной скоростей справедливо только в случае линейной зависимости скорости от времени, то есть при равноускоренном (равнозамедленном) движении. В остальных случаях его применять не желательно, так как можно получить неточный результат.

При детальном анализе мгновенных значений скоростей с помощью гистограммы, показывающей какие значения скорости попали в заданные интервалы (фигура 2), мы видим, что реально во время движения частица имела целый набор скоростей. К примеру, спидометр показывал бы все значения в диапазоне от нуля до 50 м/с. Поскольку площадь каждого столбца гистограммы пропорциональна количеству попаданий мгновенных скоростей в данный интервал группировки, то несложно сообразить, что чаще всего во время движения встречались скорости, лежащие в диапазонах (0-5) м/с. Остальные значения скорости встречались примерно одинаковое число раз.

Для определения средней скорости в этом случае удобно использовать стандартную функцию анализа данных – среднее.

Чем круче наклон кривой скорости, тем больше мгновенное ускорение

.

Введите в командное окно MATLAB програму.

Проанализируйте графики, характеризующие, как изменяется координата Y (перемещение в вертикальном направлении), мгновенные скорость и ускорение частицы, представляющей собой высокоскоростной пассажирский лифт в многоэтажном высотном здании, при поступательном неравнопеременном движении вдоль оси координат ОY.

Рис.0.3а. Лифт в многоэтажном высотном здании

Програма 14.

clear;

to=0;

t1=40;

n=1000;

Vo=10; %Задаем среднюю скорость движения лифта

ao=2;

um=Vo;

tau=t1;

Unul=0.0;

tt=linspace(to,t1,n);%Создаем переменную времени

nel=length(tt);

%Вводим логические переменные

%соответствующие временным интервалам

lp1=(tt<(0));

lp2=(tt>=0 & tt<=(3*tau/8));

lp3=(tt>(3*tau/8)& tt<=(6*tau/8));

lp4=(tt>(6*tau/8)& tt<=(tau));

%Создаем выражение, вычисляющее ординату графика

%на всех временных интервалах

uu=Unul*lp1+um.*(1-exp(-1.*tt)).*lp2+...

um.*lp3+um.*(exp(-1.*(tt-(6*tau/8)))).*lp4;

t3=linspace(to,t1,n);

Vt=uu;

Vxu=Vt(1:end-1);

delt=(t1-to)/(n);

ax=(1/delt).*diff(Vt);

axu=ax;

t=t3(1:end-1);

Xt(1)=0;

for i=1:length(t3)-1

x1=t3(1:i+1);

y1=Vt(1:i+1);

Xt(i+1)=trapz(x1,y1);

end

Xtu=Xt(1:end-1);

subplot(311);plot(t,Xtu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('Y(t), m');

subplot(312);plot(t,Vxu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('V(t), m/c');

ylim([0-0.1*um um+0.1*um])

subplot(313);plot(t,ax,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('a(t), m/c^2');

Используя графики, сделайте выводы о следующем.

1. За какое время экспрессный лифт обеспечит доставку пассажиров на высоту примерно 80 этажа (высота подъема примерно 300 метров).

2. Какой величины могут достигать максимальные изменения ускорения во время движения и разгона. Сопоставьте эти ускорения с теми, которые имеют место при движении в автомобиле и поезде, а также у военных летчиков.

Теперь рассмотрим случай, когда частица одновременно участвует в нескольких независимых движениях вдоль координат ОХ и OY, то есть совершает сложное движение, которое называется криволинейным. Зависимости полностью определяют движение частицы. Зная их, можно найти не только положения частицы, но и компоненты векторов ее скорости и ускорения по осям Ох, Оу, а следовательно модули и направления векторов в любой момент времени.

Введите в командное окно MATLAB програму.

Проанализируйте графики, характеризующие, как происходит движение частицы (фигура 1), какова траектория частицы (фигура 2) соотношения между мгновенными значениями скорости, перемещения, ускорения по координатам Х и Y и временем (фигура 3).

Посмотрите, что представляют собой графики модуля вектора скорости и ускорения, которые определяются формулой:

;

.

Сделайте вывод о том, чем характеризуют движение частицы, которая совершает сложное движение, которое называется криволинейным, то есть одновременно участвует в нескольких независимых движениях вдоль координат ОХ и OY.

Програма 15.

clear;

t=[0:0.001:10];

x=sin(t)./(t+1);

y=cos(t)./(t+1);

plot(x,y,'k--')

xlabel('Koordinata X');

ylabel('Koordinata Y');

hold on

comet(x,y)

figure

plot(x,y,'k','linewidth',2)

grid on

xlabel('Koordinata X');

ylabel('Koordinata Y');

to=0;

t1=10;

Vo=1e3;

n=1000;

t3=linspace(to,t1,n);

Xt=sin(t3)./(t3+1);

Xtu=Xt(1:end-2);

delt=(t1-to)/(n);

Vx=(1/delt).*diff(Xt);

Vxu=Vx(1:end-1);

Xtu=Xt(1:end-2);

t=t3(1:end-2);

ax=(1/delt).*diff(Vx);

Yt=cos(t3)./(t3+1);

Ytu=Yt(1:end-2);

delt=(t1-to)/(n);

Vy=(1/delt).*diff(Yt);

Vyu=Vy(1:end-1);

Ytu=Yt(1:end-2);

ay=(1/delt).*diff(Vy);

figure

subplot(321);plot(t,Xtu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('X(t), m');

subplot(323);plot(t,Vxu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('Vx(t), m/c');

subplot(325);plot(t,ax,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('ax(t), m/c^2');

subplot(322);plot(t,Ytu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('Y(t), m');

subplot(324);plot(t,Vyu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('Vy(t), m/c');

subplot(326);plot(t,ay,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('ay(t), m/c^2');

Vmod=sqrt(Vxu.*Vxu+Vyu.*Vyu);

amod=sqrt(ax.*ax+ay.*ay);

figure

subplot(211);plot(t,Vmod,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('Vmod(t), m/c');

subplot(212);plot(t,amod,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('amod(t), m/c^2');

При криволинейном сложном движении наиболее компактным способом описания траектории является кривая, описываемая концом радиус-вектора во все моменты времени - . Поэтому понятия скорости и ускорения частицы часто удобно представлять с точки зрения векторного способа описания частицы.

Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 0.3

Рис.0.4 Мгновенная скорость тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке

Введите в командное окно MATLAB програму.

Она демонстрирует, как будет двигаться частичка, брошенная с некоторой начальной скоростью под некоторым углом к горизонту. Кроме того, она показывает, что представляет собой радиус-вектора в некоторые моменты времени (фигура 1).

Сделайте вывод о том, чем характеризуют движение частицы, которая одновременно участвует в нескольких независимых движениях вдоль координат ОХ и OY.

Програма 16.

clear;

t=[0:0.001:3.45];

Vo=19.6;

gg=9.8;

alph=pi/3;

x=(cos(alph)).*Vo.*t;

y=(sin(alph)).*Vo.*t-((0.5).*gg.*t.*t);

plot(x,y,'k--')

xlabel('Koordinata X');

ylabel('Koordinata Y');

hold on

comet(x,y)

figure

XX=[ 0+i*0 0+i*0 0+i*0 ...

0+i*0 0+i*0 0+i*0 0+i*0];

YY=[ 5+i*7.4 10+i*12 17+i*14.7 ...

25+i*11.4 30+i*6 34+i*0.23 10+i*12];

godogrAB=[XX YY];

compass(godogrAB)

Скорость характеризует быстроту и направления движения частицы. Поэтому вектор скорости частицы в данный момент времени равен производной от радиус-вектора по времени

.

Модуль вектора скорости равен

.

Вектор скорости частицы в каждый конкретный момент времени направлен по касательной к траектории (при векторном способе описания движения, как демонстрирует фигура 2, траекторией будет являться кривая, описываемая концом радиус- вектора , то есть геометрическое место точек пространства, где частица побывала за время своего движения). При этом во все моменты времени в данной точке вектор направлен в сторону движения частицы.

Вектор ускорения определяет скорость изменения вектора скорости с течением времени

.

Конец вектора скорости при движении частицы описывает кривую, называемую годографом скорости. Ускорение в данной точки годографа скорости направлено по касательной к годографу в этой точке.

Если ввести координатные оси, направленные по горизонтали (ОХ) и вертикали (OY) и поместить частицу в начало координат, то в любой момент времени радиус- вектор , можно представить, как сумму двух векторов: перемещения вдоль оси ОХ и перемещения вдоль оси ОY. Эти два вектора по модулю представляют проекции на координатные оси.

Введите в командное окно MATLAB програму.

Она демонстрирует, как можно визуально представить (описать) движение частички, брошенной с некоторой начальной скоростью под некоторым углом к горизонту.

Програма 17.

clear;

t=[0:0.001:3.45];

Vo=19.6;

gg=9.8;

alph=pi/3;

x=(cos(alph)).*Vo.*t;

y=(sin(alph)).*Vo.*t-((0.5).*gg.*t.*t);

plot(x,y,'k--')

xlabel('Koordinata X');

ylabel('Koordinata Y');

hold on

comet(x,y)

figure

XX=[ 0+i*0 0+i*0 0+i*0 ...

0+i*0 0+i*0 0+i*0 0+i*0] ;

YY=[ 5+i*7.4 10+i*12 17+i*14.7 ...

25+i*11.4 30+i*6 34+i*0.23 10+i*12];

godogrAB=[XX YY];

compass(godogrAB)

figure

plot(x,y,'k','linewidth',2)

grid on

xlabel('Koordinata X');

ylabel('Koordinata Y');

to=0;

t1=3.45;

n=3450;

t3=linspace(to,t1,n);

Xt=(cos(alph)).*Vo.*t3;;

Xtu=Xt(1:end-2);

delt=(t1-to)/(n);

Vx=(1/delt).*diff(Xt);

Vxu=Vx(1:end-1);

Xtu=Xt(1:end-2);

t=t3(1:end-2);

ax=(1/delt).*diff(Vx);

Yt=(sin(alph)).*Vo.*t3-((0.5).*gg.*t3.*t3);

Ytu=Yt(1:end-2);

delt=(t1-to)/(n);

Vy=(1/delt).*diff(Yt);

Vyu=Vy(1:end-1);

Ytu=Yt(1:end-2);

ay=(1/delt).*diff(Vy);

figure

subplot(321);plot(t,Xtu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('X(t), m');

subplot(323);plot(t,Vxu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('Vx(t), m/c');

subplot(325);plot(t,ax,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('ax(t), m/c^2');

subplot(322);plot(t,Ytu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('Y(t), m');

subplot(324);plot(t,Vyu,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('Vy(t), m/c');

subplot(326);plot(t,ay,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('ay(t), m/c^2');

Vmod=sqrt(Vxu.*Vxu+Vyu.*Vyu);

amod=sqrt(ax.*ax+ay.*ay);

figure

subplot(211);plot(t,Vmod,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('Vmod(t), m/c');

subplot(212);plot(t,amod,'k','linewidth',2);grid on

xlabel('t, cek');

ylabel('amod(t), m/c^2');

Из фигуры 4 следует, что движение частицы в горизонтальном направлении происходит с постоянной скоростью (движение является равномерным), а движение в вертикальном направлении является равнопеременным (то есть с постоянным вектором ускорения).

Очевидно, что в какой-то момент времени вертикальная составляющая скорости обращается в нуль. Как свидетельствует фигура 5, в этот момент времени частица имеет наименьшую скорость. Это есть наивысшая точка подъема тела.

Нижние графики фигуры 4 свидетельствуют (с погрешностями, вызванными неточностью численных расчетов), что ускорение по горизонтальной оси равно нулю, а по вертикальной – ускорению свободного падения . Полное ускорение в любой точке траектории (показанное, с погрешностями, вызванными неточностью численных расчетов, на фигуре 5) равно по модулю и направлено вертикально вниз.

Небольшой отрезок траектории можно представить в виде дуги окружности с центром в некоторой точке О. Эту точку называют центром кривизны траектории в данной точке, а радиус окружности – радиусом кривизны траектории в той же точке. Движение частицы вдоль участка траектории может быть описано касательным в данный момент к траектории вектором и вектором нормали , перпендикулярным вектору и направленным к центру кривизны траектории. Тогда, поскольку вектор скорости частицы направлен по касательной к траектории, то его можно записать

,

где - проекция вектора на направление вектора .

Рис. 0.5 Тангенциальная (касательная) и нормальная (центростремительная) скорости

При можно записать выражение для вектора ускорения

.

Первое слагаемое называют тангенциальным (касательным) ускорением , а второе – нормальным (центростремительным) ускорением :

, .

Тангенциальное ускорение характеризует быстроту изменения значения скорости, а нормальное – быстроту изменения направления скорости.

Рис. 06. Тангенциальное (касательное) и нормальное (центростремительное) ускорение

Криволинейное движение можно представить как движение по дугам окружностей (рис. 0.7).

Рис.07. Движение по дугам окружностей

Таким образом, при движении на небольшом участке криволинейной траектории полное ускорение может быть представлено как геометрическая сумма тангенциального и нормального ускорений. Модуль вектора полного ускорения вычисляется по теореме Пифагора

.

Вектор полного ускорения лежит в плоскости, проходящей через нормаль и касательную к траектории, и направлен в сторону вогнутости траектории.

Если вернуться к рассмотренной последней задаче, то можно отметить, что в высшей точке траектории тангенциальное ускорение равно нулю ( ), а .

Эксперимент 3. Изучение основных понятий, связанных с отображением на плоскость объектов на поверхности Земли и объемных трехмерных изображений местности

Современным деловым людям приходится иметь дело с огромными объемами информации о продажах, клиентах, партнерах и конкурентах, демографии жителей, списками рассылки и многим другим. В основе этой информации лежит географическое расположение: адрес, граница зоны обслуживания, область сбыта продукции, маршрут доставки. Вся эта информация может быть отображена на карте. Если Вы при этом используете компьютерные, так называемые географические информационные системы, то это позволит Вам, создавая и анализируя картографические отображения и карты, выполнять следующее:

1. Быстро выявить по карте, где от Вас «скрываются» покупатели и конкуренты;

2. Определить наиболее выгодное для Вашего бизнеса местоположение новых производственных мощностей, филиалов и торговых точек;

3. Визуально по карте и на основе сопутствующей электронной информации провести сравнение различных характеристик по разным странам, областям и районам;

4. Нанести на карту, выделить и дополнить сопутствующей информацией зоны производства, хранения, сброса и накопления вредных для людей и живых организмов веществ и материалов;

5. Проводить вычисление площадей, длин, периметров картографических объектов, расстояний между ними;

6. Выполнять анализ поверхностей (расчлененность рельефа углы склонов);

7. Осуществлять визуализацию поверхностей как в изопроекциях, так и на топографической карте;

8. Выполнять отбор объектов, находящихся внутри/вне некоторого контура (контуров) по заданным условиям (больше, меньше, равно, не равно);

9. Определять ближайших соседей.

Таким образом, для эффективной работы экономисту необходимы умения понимать, как применяются карты для анализа информации.

Вы уже многократно слышали, что Земля является сферой. Предположение о том, что Земля имеет сферическую форму, было высказано в те времена, когда жили еще древние греки. Эту идею (ее предписывают Пифагору) они основывали на философских выводах - сфера имеет наиболее совершенную форму. В доказательство того, что Земля не плоская, а круглая, внес свой вклад Аристотель и многие другие ученые. Убедитесь в этом сами!

Введите в командное окно программу.

Програма 18.

clear;

h(1)=axes('Position', [0, 0, 0.8 1.2]);

sphere

Когда идее о том, что Земля имеет форму совершенной сферы насчитывалось почти 2000 лет, Исаак Ньютон внес некоторые дополнения. Рассуждал он следующим образом: чем больше скорость вращения, тем сильнее центробежный эффект – то есть тенденция отбросить материю дальше от центра вращения. Из этого следовало, что центробежный эффект увеличивается от нуля на неподвижных полюсах до максимального на быстро вращающемся экваториальном поясе. Это значит, что Земля должна представлять собой сплюснутый сфероид с экваториальной выпуклостью и сжатый у полюсов. Ее форма должна напоминать скорее мандарин, чем мяч. Ньютон даже смог вычислить, что сплюснутость у полюсов составляет 1/230 от общего диаметра Земли (рис.1.1).

Рис. 1.1. Изменение представлений о форме Земли: в античные времена и в 17 веке

Если смотреть на Землю из космоса, то она кажется правильной сферой. Но на поверхности Земли имеются горы, овраги и прочее, которые создают отклонения от совершенной формы сферы.

Дальнейшие исследования показали, что форма Земли еще более сложная, чем фигура, сплюснутая у полюсов и выпяченная на экваторе (рис. 1.2). Поэтому, если быть точным, Земля в настоящее время предстает перед нами в форме некой «глыбы».

Рис. 1.2. Представления о форме Земли в настоящее время

Как давно известно, масса в глубинах земного шара распределена неравномерно и неодинакова в разных районах планеты. Поэтому на напряженность гравитационного поля, создаваемого планетой, влияет множество факторов, таких как наличие и высота гор, выпуклость в зоне экватора, неоднородность состава земной коры и т.д..  По этой причине фигуру Земли удобно представить, вообразив такую поверхность, у которой в каждой точке сила тяжести направлена по нормали к ней, то есть по отвесной линии. Такую поверхность называют уровневой.

Сложную фигуру нашей планеты, ограниченную уровневой поверхностью, проходящей через точку, закрепленную на высоте среднего уровня моря и являющуюся началом отсчета высот, называют геоидом. Геоид это некое эмпирическое приближение к Земле, которое представляет фигуру Земли, сглаженную до уровня мирового океана, без учета деталей рельефа (рис.1.3). Иначе говоря, геоид представляется в виде поверхности идеального Мирового океана при отсутствии ветров, приливов и течений, формирующуюся только под действием силы тяжести.

Рис. 1.3. Соотношение различных поверхностей, аппроксимирующих Землю

Стартовавший в 2009 году европейский спутник GOCE (Gravity Field and Steady-State Ocean Circulation Explorer — исследователь гравитационного поля и установившихся океанских течений) за два года работы в космосе, измеряя притяжение Земли, набрал достаточно данных, чтобы составить гравитационную карту беспрецедентной точности. Аппарат-«исследователь», GOCE, обладая шестью акселерометрами, в сто раз более чувствительными, чем любые поднимавшиеся на орбиту, летает по самой низкой орбите из всех современных научных спутников — всего 254,9 километра над Землёй (рис1.3а).

Рис. 1.3а. Европейский спутник GOCE (Gravity Field and Steady-State Ocean Circulation Explorer — исследователь гравитационного поля и установившихся океанских течений)

Это один из секретов его высокой чувствительности к колебаниям гравитационного поля планеты. Он может почувствовать отклонение в притяжении в одну десятитриллионную от нормального уровня. Потому «гоче» способен определить форму геоида с точностью в 1-2 сантиметра по высоте на 100-километровом отрезке. Она поможет учёным раскрыть многие интересные аспекты «функционирования» нашей планеты.

По результатам работы GOCE получен геоид, показанный на рис. 1.3б.

Рис. 1.3.б Фрагмент новой карты геоида. Самая сильная гравитация — в районах, окрашенных жёлтым цветом, самая слабая — на синих участках. Форма геоида намеренно усиленна — для большей наглядности различия высот умножены в 10 тысяч раз.

Рис.1.3в. Схема, отображающая характер деформации формы Земли по данным космической лазерной дальнометрии НАСА. Image 1 – характер деформации формы Земли до 1998 г.; Image 2 – характер деформации формы Земли начиная с 1998 г. по настоящее время.

Чтобы Вам стала более понятной фигура геоида, предварительно посмотрите, как средствами трехмерной графики (3-D) представляют некую абстрактную поверхность.

Введите программу.

Програма 19.

clear;

[X,Y]=meshgrid(-2:0.1:2);

Z=-10*X.*exp(-X.^2-Y.^2);

surf (X,Y,Z)

colorbar('horiz')

Эту абстрактную трехмерную поверхность, представленную на графике, можно трактовать, как часть земной поверхности, которая имеет возвышение и углубление. Чтобы установить соответствие между цветом точки, изображенной на поверхности, и высотой этой точки внизу графика появляется линейка с цветовой палитрой и цифрами определяющими значение высоты.

Введите программу и посмотрите, как выглядит геоид Земли при представлении его на плоскости.

Введите программу.

Програма 20.

clear;

load geoid;

load coast

figure;

axesm eqdcylin

meshm(geoid,geoidlegend)

colorbar('horiz')

plotm(lat,long,'k')

При картографировании, при выполнении практических расчетов сложную фигуру геоида заменяют математически более простой – эллипсоидом вращения – геометрическим телом, которое образуется при вращении эллипса вокруг малой оси (рис. 1.4). Как свидетельствует рисунок, чтобы с такой поверхностью можно было работать, необходимо знать его основные параметры: большая полуось a, малая полуось b, полярное сжатие (a-b)/a.

Рис.1.4. Двухосный эллипсоид

Разрез эллипсоида, показанный на рис. 1.5, демонстрирует наиболее важные его три параметра, используемые в англоязычной литературе.

Рис.1.5. Эллипсоид в разрезе и его параметры

1. Ось вращения (Axis of rotation), относительно которой вращается эллипсоид, отображающий Землю.

2. Малая полярная ось (Semi minor polar axis).

3. Большая экваториальная ось (Semi major equatorial axis).

В настоящее время известно много эллипсоидов, представляющих Землю.

В СССР в 1940 году расчет эллипсоида был выполнен выдающимся ученым Ф. В. Крассовским (1878-1948) и его учеником А. А. Изотовым (1907-1988).

Международными астрономо-геодезическими организациями применялись эллипсоиды (GRS-67 – Geodetic Reference System, 1967), WGS-72 (World Geodetic System, 1972). В настоящее время параметры современной точности имеют эллипсоид системы GRS- 80, (Geodetic Reference System, 1980), WGS - 84 (World Geodetic System, 1984), получивший мировое распространение благодаря американской глобальной системе спутникового позиционирования и российский эллипсоид ПЗ – 90 (Параметры Земли, 1990).

Введите программу

Програма 21.

clear;

disp( ' ')

format long

disp( 'Радиус Земли, как сферы, в км: ')

almanac('earth','sphere','kilometers')

disp( 'Большая полуось Земли, как эллипсоида, в км: ')

disp( 'Первый эксцентриситет меридионального эллипса, в км: ')

ellips1 = almanac('earth','ellipsoid','kilometers')

disp( 'Большая полуось , как эллипсоида в wgs72, в км: ')

disp( 'Первый эксцентриситет меридионального эллипса, в км: ')

wgs72 = almanac('earth','wgs72')

disp( 'Малая полярная ось в wgs72, в км: ')

semiminorwgs72 = minaxis(wgs72)

disp( 'Большая полуось , как эллипсоида в grs80, в км: ')

disp( 'Первый эксцентриситет меридионального эллипса, в км: ')

grs80 = almanac('earth','grs80')

disp( 'Малая полярная ось в grs80, в км: ')

semiminorgrs80 = minaxis(grs80)

format short

Различают общеземной эллипсоид, наилучшим образом подходящий для решения глобальных картографо-геодезических задач, и референц - эллипсоиды, используемые в отдельных регионах и странах. Применение локальных эллипсоидов, наилучшим образом соответствующих данному региону, это не только дань традиции, но и потребность иметь наиболее удобный для данной территории эллипсоид, когда уклонения отвесных линий от нормалей к нему минимальны (рис. 1.6)

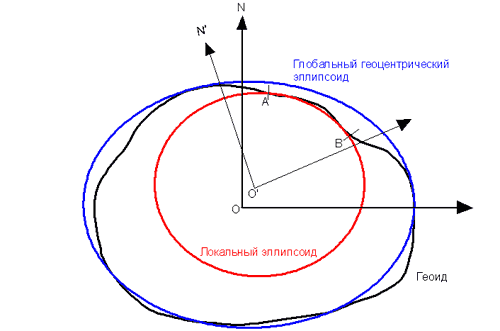
Рис. 1.6. Соотношение различных эллипсоидов, аппроксимирующих Землю

WGS 84 определяет координаты относительно центра масс Земли, погрешность составляет менее 2 см.

В WGS84, нулевым меридианом считается «IERS Reference Meridian». Он расположен на 5,31” к востоку от Гринвичского меридиана. За основу взят сфероид с большим радиусом — 6 378 137 м (экваториальный) и меньшим — 6 356 752,314245 м (полярный). Отличается от геоида менее чем на 200 м.

Для определения местоположения объектов на поверхности Земли используется географическая (или геодезическая) система координат (ГСК). Она использует трехмерную сферическую поверхность. Положение любой точки на земном эллипсоиде определяется широтой и долготой (рис.1.7).

Широта и долгота - это углы, вершина которых расположена в центре Земли, а одна из сторон проходит через точку на земной поверхности. Углы, как правило, измеряются в градусах (или в градах).

Надо иметь в виду, что в сферической системе используются «горизонтальные линии» или линии, соответствующие направлению восток-запад. Это линии равной широты, или параллели (рис.1.6а). «Вертикальные линии», или линии идущие в направлении с юга на север, - это линии равной долготы, или меридианы (рис.1.6а). Эти линии опоясывают глобус и образуют сеть географической координатной привязки, называемую картографической сеткой.

Рис. 1.6а. Параллели, меридианы и картографическая сетка

Линия широты, которая расположена посередине между полюсами, носит название экватора. Она соответствует линии нулевой широты. Линия нулевой долготы носит название нулевого (или начального) меридиана. Для большинства географических систем координат нулевой меридиан это линия долготы, проходящая через обсерваторию Гринвич в Англии. Некоторые страны используют в качестве нулевых меридианов линии долготы, проходящие через Берн, Боготу или Париж.

Начальная точка картографической сетки (0,0) определяется местом пересечения экватора и нулевого меридиана. Затем глобус делится на четыре географических квадранта (четверти шара), которые определяются показаниями компаса в начальной точке. Север и юг расположены соответственно выше и ниже экватора, а запад и восток соответственно слева и справа от нулевого меридиана.

Если быть более точным, то значения широты и долготы, как правило, измеряются либо в десятичных градусах, либо в градусах, минутах, секундах (DMS). Значения широты отсчитываются относительно экватора и могут изменяться от 90° на Южном полюсе до +90° на Северном полюсе.

Значения долготы отсчитываются относительно нулевого меридиана. Они могут меняться от _180° при движении на запад от нулевого меридиана и до 180° придвижении на восток от нулевого меридиана. Если за нулевой меридиан принят Гринвич, то координаты в Австралии, расположенной к югу от экватора и к востоку от Гринвича, будут иметь положительные значения долготы и отрицательные значения широты.

Широта (Latitude) – угол , образованный плоскостью, нормальной к поверхности земного эллипсоида и проходящей через данную точку А, и плоскостью его экватора (рис1.7). По-другому – широта это угловое расстояние от экватора.

Линия экватора – след сечения эллипсоида плоскостью, проходящей через его центр.

Рис.1.7. Определение положения точки А на земном эллипсоиде широтой и долготой

Широта отсчитывается от линии экватора (рис.1.8) в градусах ( 180^О). На плоских картах линии широты – это горизонтальные линии сетки.

Рис.1.8. Земной шар с сеткой для отсчета широты: рассекая эллипсоид плоскостями, проходящими перпендикулярно полярной оси, получают линии параллелей

Широту указывают, как северную (N) или как южную (S). Например, 45N –это 45 градусов северной широты, а 30S – 30 градусов южной широты (рис. 1.9).

Рис.1.9. Отсчет широты и долготы на эллипсоиде

Долгота (Longitude) – двухгранный угол между плоскостями меридианов данной точки и начального меридиана (рис.1.7). Имеется начальный меридиан, от которого принято отсчитывать долготу (рис.1.10). Долгота отсчитывается в градусах ( 180^О) от Гринвичского меридиана. Этот меридиан и долгота 180^О делят земной шар на восточное и западное полушарие (рис). Долгота 1-180 это восточная (Е) долгота, а от -0 до западная (W) долгота (рис.1.9).

Рис. 1.10. Земной шар с сеткой для отсчета долготы: рассекая эллипсоид плоскостями, проходящими через ось вращения, получают линии меридианов. Линии меридианов тянутся от полюса к полюсу.

Сетка меридианов и параллелей на земном эллипсоиде, шаре или на глобусе называется географической сеткой.

При создании и использовании карт приходится определять длины параллелей и меридианов.

Наиболее просто вычисляется длина дуги параллели. Параллель – окружность; ее длина меду двумя точками с долготами и равна произведению радиуса этой параллели на разность долгот, выраженных в радианной мере:

.

Меридиан- эллипс, поэтому вычисление его длин дуг более сложно. Длину дуги меридиана между двумя точками с широтами В₁ и В₂ определяют формулой

,

где М – радиус кривизны меридиана при широтах В₁ и В₂ и средней широте.

Погрешность расчета длины дуги составляет 1-2 см при длинах дуг до 500 км.

Для решения задач на эллипсоиде необходимо использовать довольно громоздкие формулы. Поэтому в ряде случаев, когда точность позволяет, эллипсоид или его часть заменяют шаром.

При замене эллипсоида шаром нужно выбрать подходящий радиус шара и перейти от широт (В) и долгот (L) эллипсоида к широтам ( ) и долготам ( ) на шаре. Обычно берут , а радиус шара 6371 км (рис.1.11). При этом шаре дуга меридиана между экватором и полюсом на 5,5 км (0,05%) длиннее, а дуга четверти экватора на 11б2 км (0,1%) короче, чем на эллипсоиде.

Рис. 1.10. Земной шар в виде сферы, используемый для решения практических задач

Земной шар – трехмерный объект. Карты, которыми пользуются люди, это листы – плоские объекты. Если попытаться разрезать бумагу на глобусе, то окажется, что невозможно получить карту в виде обычного листа бумаги: она окажется в виде лоскутов с большими промежутками между ними. Поэтому приходится идти на различные ухищрения, чтобы сделать привычные нам плоские карты Земли. Чаще всего используют метод проекций. Проекция устанавливает однозначное соответствие между геодезическими координатами (широтой В и долготой L) и их прямоугольными координатами (X и Y) на карте. Проекции получают путем проектирования Земного шара на ту или иную поверхность. При этом при изыскании любых картографических проекций исходят из аксиомы, которая состоит в том, что сферическую поверхность Земного шара (эллипсоида) нельзя развернуть на плоскости карты без искажений.

Спроецированная система координат является производной от географической системы координат, которая основывается на сфере или сфероиде.

В спроецированной системе координат местоположения определяются координатами x, y на сетке с началом координат в центре сетки. Положение каждой точки определяется двумя координатами, определяющими ее положение относительно центра. Одно определяет его положение по горизонтали, а другое – его положение по вертикали. Эти два значения называются координатой x и координатой y. Если использовать эти обозначения, то начальные координаты имеют значения x=0 и y=0.

На регулярной сетке из отстоящих на одинаковом расстоянии друг от друга горизонтальных и вертикальных линий, горизонтальная линия в центре называется осью x, а центральная вертикальная линия – осью y. Единицы измерения постоянны и имеют равные интервалы во всем диапазоне x и y. Горизонтальным линиям выше начала координат и вертикальным линиям справа от начала координат приписываются положительные значения; линиям ниже или слева – отрицательные значения. Четыре квадранта представляют четыре возможные комбинации положительных и отрицательных x- и y-координат.

По характеру искажений могут быть проекции следующих видов.

1. Равновеликие проекции сохраняют площади без искажений. Такие проекции удобны для изменения площадей объектов. Равновеликие проекции сохраняют площадь изображаемых объектов. Однако в них значительно нарушены углы и формы, что особенно заметно для больших территорий. Вследствие этого другие свойства: форма, углы, масштаб - искажаются. В равновеликих проекциях параллели и меридианы могут не пересекаться под правильными углами. Например, на карте мира приполярные области выглядят сильно сплюснутыми. В некоторых случаях, особенно на картах небольших территорий, искажение форм не является очевидным.

2. Равноугольные проекции – оставляют без искажения углы и формы контуров, показанных на карте. Элементарная окружность в таких проекциях остается окружностью, но размеры ее сильно меняются. Такие проекции удобны для определения направлений и прокладки маршрутов по заданному азимуту, поэтому их всегда используют в навигационных картах. Зато карты, составленные в равноугольных проекциях, имеют значительные искажения площадей.

Равноугольные проекции сохраняют без искажений малые локальные формы. Для сохранения отдельных углов, описывающих пространственные отношения, равноугольная проекция должна также представлять линии картографической сетки пересекающимися под углом 90° на карте. Это достигается в этой проекции с помощью сохранения всех углов. Недостаток заключается в том, что площадь, ограниченная рядом кривых, может быть в процессе преобразования значительно искажена. Ни одна из картографических проекций не может сохранять большие территории без искажения формы.

Чтобы добиться наименьших искажений применяют также способ двойного проектирования: сперва эллипсоид проектируют на шар, а затем шар – на плоскость. Компьютерные технологии позволяют рассчитывать проекции с заданными свойствами с учетом искажений, поэтому в настоящее время известно более 60 способов такого проектирования.

Вспомогательными поверхностями при переходе от эллипсоида или шара к карте могут быть цилиндр, конус или плоскость. Поэтому в картографии основными являются три типа проекций: цилиндрическая; коническая; азимутальная.

Цилиндрические проекции - проектирование шара (помещенного внутрь цилиндра) ведется на поверхность цилиндра, а его боковая поверхность разворачивается в плоскость. Если пояснять по-другому, то все точки поверхности шара переносятся на внутреннюю поверхность цилиндра, а затем цилиндрическая поверхность расправляется в плоскость.

Если ось цилиндра совпадает с осью вращения Земли, а его поверхность касается шара по экватору, то проекция называется нормальной (прямой) цилиндрической. При этом меридианы предстают в виде равноотстоящих параллельных прямых, а параллели, в виде прямых, перпендикулярных к ним. В таких проекциях меньше всего искажений в тропических и приэквоториальных областях.

Если ось цилиндра расположена в плоскости экватора, то это поперечная цилиндрическая проекция. Цилиндр касается шара по меридиану, искажения вдоль него отсутствуют, и, следовательно, в такой проекции выгодно изображать территории, вытянутые с севера на юг. Поперечные цилиндрические проекции, такие как Поперечная проекция Меркатора, используют меридианы как линии касательного

контакта или линии, параллельные меридианам, как линии сечения.

Рис. 1.10. Изображение территории России, вытянутой с севера на юг в поперечной цилиндрической проекции

Програма 22.

clear; close all;

clear all;

load russia

[latlim,longlim] = limitm(map,refvec)

Введите программу.

Посмотрите, что представляют собой оси нормальной (прямой) равнопромежуточной и поперечной цилиндрической проекции Меркатора

Програма 23.

close all;

clear all;

axesm eqdcylin

framem on; gridm on; mlabel on; plabel on

setm(gca,'LabelFormat','signed')

figure;

axesm mercator

framem on; gridm on; mlabel on; plabel on

setm(gca,'LabelFormat','signed')

Введите программу.

Посмотрите, как выглядит в соответствующих цилиндрических проекциях изображение карты и множества окружностей, преобразуемых в соответствующие проекции. Размеры и форма кругов-проекций характеризует искажения площадей и углов (форм).

Для нормальной (прямой) равнопромежуточной цилиндрической проекции:

Програма 24.

close all;

clear all;

load coast;

axesm ('eqdcylin','MapLatLimit',[-50 180], ...

'MapLonLimit',[-50 180])

framem on;

gridm on;

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

figure;

axesm ('eqdcylin','MapLatLimit',[-50 180], ...

'MapLonLimit',[-50 180])

framem on;

gridm on;

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

tissot

Для поперечной цилиндрической проекции Меркатора:

Програма 25.

close all;

clear all;

load coast;

axesm ('mercator','MapLatLimit',[-50 180], ...

'MapLonLimit',[-50 180])

framem on;

gridm on;

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

figure;

axesm ('mercator','MapLatLimit',[-50 180], ...

'MapLonLimit',[-50 180])

framem on;

gridm on;

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

tissot

Коническая проекция получается проектированием всех точек шара, лежащего внутри конуса, на его внутреннюю поверхность. При этом поверхность шара (эллипсоида) проектируется на поверхность касательного или секущего конуса, после чего она как бы разрезается по образующей и разворачивается в плоскость.

Также различают нормальную (прямую) коническую проекцию, когда ось конуса совпадает с осью вращения земли, поперечную коническую – ось конуса лежит в плоскости экватора и косую коническую – если ось конуса наклонена к плоскости экватора. Введите программу.

Посмотрите, что представляют собой оси конической проекций

Програма 26.

close all;

clear all;

axesm lambert

framem on; gridm on; mlabel on; plabel on

setm(gca,'LabelFormat','signed')

figure;

axesm eqaconic

framem on; gridm on; mlabel on; plabel on

setm(gca,'LabelFormat','signed')

Введите программу.

Посмотрите, как выглядит в конической проекции Ламберта изображение карты и множества окружностей, преобразуемых в соответствующие проекции. Размеры и форма кругов-проекций характеризует искажения площадей и углов (форм).

Програма 27.

close all;

clear all;

load coast;

axesm ('lambert','MapLatLimit',[-50 180], ...

'MapLonLimit',[-50 180])

framem on;

gridm on;

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

figure;

axesm ('lambert','MapLatLimit',[-50 180], ...

'MapLonLimit',[-50 180])

framem on;

gridm on;

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

tissot

Введите программу.

Посмотрите, как выглядит в эквидистантой конической проекции изображение карты и множества окружностей, преобразуемых в соответствующие проекции. Размеры и форма кругов-проекций характеризует искажения площадей и углов (форм).

Програма 28.

close all;

clear all;

load coast;

axesm ('eqaconic','MapLatLimit',[-50 180], ...

'MapLonLimit',[-50 180])

framem on;

gridm on;

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

figure;

axesm ('eqaconic','MapLatLimit',[-50 180], ...

'MapLonLimit',[-50 180])

framem on;

gridm on;

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

tissot

В нормальной конической проекции меридианы представляют собой прямые линии, расходящиеся от точки полюса, а параллели – дуги концентрических окружностей.

Воображаемый конус касается Земного шара и сечет его в районе средних широт, поэтому в такой проекции удобнее всего картографировать вытянутые с запада на восток в средних широтах территории России, Канады, США.

Введите программу.

Програма 29.

close all;

clear all;

figure

worldmap('lo','russia','patch')

figure

worldmap('lo','canada','patch')

figure

worldmap('lo','USA','patch')

figure

worldmap('lo','Ukraine','patch')

Азимутальная проекция получается, когда поверхность Земного шара переносится на касательную или секущую плоскость. Если плоскость перпендикулярна к оси вращения Земли, то получается нормальная (полярная азимутальная проекция). Параллели в ней являются концентрическими окружностями, а меридианы – радиусами этих окружностей. В этой проекции картографируют приполярные области. Если плоскость проекции перпендикулярна к плоскости экватора, то получается поперечная (экваториальная азимутальная проекция). Она всегда используется для карт полушарий. А если проектирование выполнено на касательную или секущую вспомогательную плоскость, находящуюся под любым углом к плоскости экватора, то получается косая азимутальная проекция.

Введите программу.

Посмотрите, как выглядит в косой азимутальной проекции изображение карты и множества окружностей, преобразуемых в соответствующие проекции. Размеры и форма кругов-проекций характеризует искажения площадей и углов (форм).

Програма 30.

close all;

clear all;

load coast;

axesm ('eqaazim','MapLatLimit',[-50 180], ...

'MapLonLimit',[-50 180])

framem on;

gridm on;

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

figure;

axesm ('eqaazim','MapLatLimit',[-50 180], ...

'MapLonLimit',[-50 180])

framem on;

gridm on;

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

tissot

Следует иметь в виду, что топографические карты России создают в поперечно-цилиндрической проекции Гаусса-Крюгера, а США и многие другие западные страны – в универсальной поперечно-цилиндрической проекции Меркатора (сокращенно UTM). Обе проекции близки по своим свойствам.

Морские и аэронавигационные карты всегда даются исключительно в цилиндрической проекции Меркатора.

Важным элементом математической основы карт является координатная сетка. Она необходима для ориентирования по карте, определения направлений, нанесения новых объектов по их координатам. Кроме того, наличие сетки позволяет судить о масштабе карты, о виде проекции и распределении искажений в ней. Сетка делает карту картой. Говорят даже, что «карта без сетки все равно, что термометр без шкалы».

Чаще всего на карту наносится картографическая сетка – изображение на карте линий меридианов и параллелей (географической сетки), отражающих значения долгот, счет которых ведется от начального Гринвичского меридиана, и широт, которые отсчитываются от экватора. Картографическая сетка имеет важный географический смысл: она показывает направления «север – юг» и «запад – восток», позволяет судить о широтных поясах. Линии географической сетки на картах наносят обычно через равные интервалы. Это зависит от масштаба и назначения карты.

Введите программу.

Посмотрите, какой вид имеет картографическая сетка на картах, на которых изображены Украина и Россия. Посмотрите, какой диапазон долгот и широт имеет изображение карты России.

Програма 31.

close all;

clear all;

figure;

worldmap Ukraine

figure;

worldmap russia

load russia

[latlim,longlim] = limitm(map,refvec)

На картах обычно имеется масштаб - степень уменьшения объектов на карте относительно их размеров на земной поверхности (точнее на поверхности эллипсоида). В связи с переходом от сферической поверхности планеты к плоскому изображению, на географических картах масштаб меняется от места к месту. На картах различают главный и частные масштабы.

Главный масштаб показывает, во сколько раз линейные размеры на карте уменьшены по отношению к эллипсоиду или шару. Этот масштаб подписывают на карте. При этом необходимо иметь в виду, что он справедлив лишь для отдельных линий и точек.

Частный масштаб отражает соотношения размеров объектов на карте и эллипсоиде (шаре) в данной точке.

Введите программу.

Посмотрите, какой вид имеет на картах линейный (графический) масштаб в морских милях и километрах, который представляется в виде линейки, разделенной на равные части, с подписями, означающими соответствующие расстояния на местности.

Програма 32.

close all;

clear all;

worldmap('guatemala','patchonly')

scaleruler

setm(handlem('scaleruler1'),'YLoc',.205)

scaleruler('units','nm')

setm(handlem('scaleruler2'),...

'MajorTick',0:100:300,'MinorTick',0:25:50,...

'TickDir','down','MajorTickLength',km2nm(20),...

'MinorTickLength',km2nm(12.5))

setm(handlem('scaleruler2'),'RulerStyle','patches')

Введите программу.

Посмотрите, какой вид на картах Украины и Белоруссии будет иметь линейный (графический) масштаб в морских милях и километрах.

Програма 33.

close all;

clear all;

figure;

worldmap('Ukraine','patchonly')

scaleruler

scaleruler('units','nm')

setm(handlem('scaleruler2'),...

'MajorTick',0:100:200,'MinorTick',0:25:50,...

'TickDir','down','MajorTickLength',km2nm(20),...

'MinorTickLength',km2nm(12.5))

setm(handlem('scaleruler2'),'RulerStyle','patches')

figure;

worldmap('belarus','patchonly')

scaleruler

scaleruler('units','nm')

setm(handlem('scaleruler2'),...

'MajorTick',0:100:200,'MinorTick',0:25:50,...

'TickDir','down','MajorTickLength',km2nm(20),...

'MinorTickLength',km2nm(12.5))

setm(handlem('scaleruler2'),'RulerStyle','patches')

При работе со сферическими объектами различают так называемые большие и малые круги.

Любое сечение сферы пополам плоскостью, проходящей через центр сферы, образует большой круг, а окаймляющая его линия является большой окружностью. Экватор и все меридианы являются большими окружностями. Через любые две точки сферы можно провести большую окружность. Линия этой окружности будет задавать кратчайшее расстояние между этими точками.

Теперь представьте себе, что вы взяли в руки большой циркуль и нарисовали окружность на большом глобусе. При этом любую точку сферы можно сделать центром подобной окружности. Проведенная таким образом окружность образует малый круг, а окаймляющая его линия является малой окружностью.

Введите программу.

Посмотрите, какой вид на сфере будет иметь большая и малые окружности

Програма 34.

close all;

clear all;

figure;

axesm ortho; gridm on; framem on

setm(gca,'Origin', [45 30 30], 'MLineLimit', [75 -75],...

'MLineException',[0 90 180 270])

B = [0 60];

C = [0 30];

scb = scircle2(B(1), B(2), 0, 150);

scc = scircle1('rh',C(1), C(2), 20);

plotm(B(1), B(2),'bo','MarkerFaceColor','b')

plotm(C(1), C(2),'mo','MarkerFaceColor','m')

plotm(scb(:,1), scb(:,2),'b')

plotm(scc(:,1), scc(:,2),'m')

textm(4.5,-10,'Loxodromic Small Circle')

textm(4,-6,'(30\circ from point C')

textm(-2,-4,'in rhumb line sense)')

textm(40,-60,'Great Circle as Small Circle')

textm(45,-50,'(90\circ from point B)')

На карте можно всегда проложить след. След – это линия, проведенная через заданные точки – начальную и конечную.

Рис. 1.11. След, проходящий через две точки

Введите программу.

Посмотрите, какой вид будет иметь след на карте, проведенный между г. Львов (50N,24E) и Мариуполь (47N,37E) при вычислении его по большой окружности (фигура 2). Для того, чтобы легче было ориентироваться, приводится также изображение, демонстрирующее положение Украины на карте (фигура 1).

Програма 35.

close all;

clear all;

figure;

worldmap Ukraine

figure;

load coast;

axesm ('eqdcylin','MapLatLimit',[40 60], ...

'MapLonLimit',[15 43])

framem on;

gridm('MLineLocation',5,'PLineLocation',5);

mlabel('MLabelLocation',5)

plabel('PLabelLocation',5)

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

[latgc,longc] = track2('gc',47,37,50,24);

plotm(latgc,longc,'k')

Введите программу.

Посмотрите, какой вид будет иметь след на карте, проведенный между г. Львов и г. Мариуполь при вычислении его по малой окружности.

Програма 36.

close all;

clear all;

figure;

worldmap Ukraine

figure;

load coast;

axesm ('eqdcylin','MapLatLimit',[40 60], ...

'MapLonLimit',[15 43])

framem on;

gridm('MLineLocation',5,'PLineLocation',5);

mlabel('MLabelLocation',5)

plabel('PLabelLocation',5)

setm(gca,'LabelFormat','signed')

plotm(lat,long,'b')

[latgc,longc] = track2('rh',47,37,50,24);

plotm(latgc,longc,'k')

Введите программу.

Посмотрите, какой вид будет иметь след на карте, проведенный между тремя городами

Програма 37.

close all;

clear all;

load coast

axesm mollweid

framem('FEdgeColor','blue','FLineWidth',0.5)

plotm(lat,long,'LineWidth',1,'Color','blue')

citylats = [30 -23 -32];

citylongs = [32 -43 116];

plotm(citylats,citylongs,'r*')

[gclat,gclong] = track2('gc',citylats(1),citylongs(1),...

citylats(2),citylongs(2));

[rhlat,rhlong] = track2('rh',citylats(1),citylongs(1),...

citylats(3),citylongs(3));

plotm(gclat,gclong,'m-');

plotm(rhlat,rhlong,'m-')

Введите программу.

Посмотрите, как отличаются следы на карте, проведенные между г. Львов и г. Мариуполь при вычислении их по большой и малой окружности.

Проанализируйте, каково расстояние между городами, когда их местоположение заданны значениями географических координат. Расстояние определяется по дуге большой окружности, к которой принадлежат точки, и по малой.

Оцените азимут – угол между плоскостью меридиана данного объекта и плоскостью, проходящей через эту точку

Рис. 1.11. След, определяемый известным азимутом и расстоянием от координат начальной точки

Програма 38.

close all;

clear all;

axesm('mercator','MapLatLimit',[40 60],'MapLonLimit',[15 43])

[lattrkgc,lontrkgc] = track2(47,37,50,24);

[lattrkrh,lontrkrh] = track2('rh',47,37,50,24);

plotm(lattrkgc,lontrkgc,'b')

plotm(lattrkrh,lontrkrh,'k')

axesm('mercator','MapLatLimit',[40 60],'MapLonLimit',[15 43])

[lattrkgc,lontrkgc] = track2(47,37,50,24);

[lattrkrh,lontrkrh] = track2('rh',47,37,50,24);

plotm(lattrkgc,lontrkgc,'b')

plotm(lattrkrh,lontrkrh,'k')

disp( 'Расстояние между городами по большой дуге, в км: ')

distgc =deg2km (distance(47,37,50,24))

disp( 'Расстояние между городами по малой дуге, в км: ')

distrh = deg2km (distance('rh',47,37,50,24))

disp( 'Отличие расстояний между городами , в км: ')

kmdifference = (distrh-distgc)

disp( 'Азимут между городами по большой дуге, в град: ')

azgc = azimuth(37,24,47,50)

disp( 'Азимут между городами по малой дуге, в град: ')

azrh = azimuth('rh',37,24,47,50)

Для отображения информации могут использоваться объемные (3D) рельефные карты - карты, дающие объемное трехмерное изображение местности.

Введите программу.

Посмотрите, как выглядит фрагмент рельефа, представленный в объемном трехмерном виде (фигура 2), и его вид сверху, окрашенный цветами, соответствующими высоте (фигура 1)

Програма 39.

close all;

clear all;

figure

h = mapshow('9129CATD.ddf','DisplayType','mesh');

Z = get(h,'ZData');

colormap(demcmap(Z))

figure

mapshow('9129CATD.ddf');

colormap(demcmap(Z))

view(3); % View as a 3-d surface

axis normal;

Введите программу.

Посмотрите, как выглядит фрагмент рельефа земного геоида, представленный в объемном трехмерном виде.

Програма 40.

close all;

clear all;

load topo

load geoid

axesm gstereo

meshm(geoid,geoidlegend,size(geoid),topo);

load coast

plotm(lat,long,'k')

zdatam(handlem('allline'),1000)

tightmap

daspectm('m',200); tightmap

view(20,35)

set(gca,'Box','off')

camlight;

lighting phong

set(gca,'projection','perspective')

Введите программу.

Посмотрите, как выглядит фрагмент рельефа области Кореи в объемном трехмерном виде (фигура 2), и его вид сверху, окрашенный цветами, соответствующими высоте (фигура 1).

Програма 41.

close all;

clear all;

load korea

[lat,lon] = meshgrat(map,maplegend);

map = km2deg(map/1000);

axesm('MapProjection','eqaconic','MapParallels',[],...

'MapLatLimit',[30 45],'MapLonLimit',[115 135])

surfm(lat,lon,map,map); demcmap(map)

figure;

load korea

[lat,lon] = meshgrat(map,maplegend);

map = km2deg(map/1000);

axesm('MapProjection','eqaconic','MapParallels',[],...

'MapLatLimit',[30 45],'MapLonLimit',[115 135])

surfm(lat,lon,map,map); demcmap(map)

view(60,30)

Рельефные карты удобны тем, что позволяют решать некоторые специфические задачи. В частности их использование позволяет построить профиль поверхности вдоль пути относительно уровня моря.

Введите программу.

Когда появиться изображение, то мысленно определите посредством двух точек линию, вдоль которой Вы хотите построить профиль. Мышкой наведите перекрестье в первую точку и щелкните левой кнопкой мышки. Затем с помощью мышки наведите перекрестье во вторую точку и опять щелкните левой кнопкой мышки. После этого нажмите на кнопку «Enter» клавиатуры. Вы увидите график профиллограммы пути, на котором каждой точке на линии пути (абсциссе) соответствует высота местности относительно уровня моря.

Програма 42.

close all;

clear all;

load korea

worldmap(map,refvec,'dem')

colorbar('horiz')

mapprofile